MAP 是最大后验概率的缩写。后验概率指的是当有一定观测结果的情况下,对其他随机变量进行推理。假设随机变量的集合为X ,观察到的变量为 e, W = X-e , AP = P(W|e). 后验概率和联合概率是不同的两个概念。事实上,后验概率更接近推理本身的“意义”,并且被越来越多的用于诊断系统中。在医疗诊断系统中,存在包括病症,症状等许多随机变量,使用VE或者消息传递之类的推理手段确实可以获得每个随机变量的概率以及某些随机变量的联合概率(一个Scope的概率)。但实际上,如果面对某些很少出现的症状以及对应病症,联合概率密度函数并不合适,比如病人红细胞减少的概率非常小,但红细胞减少很大几率上对应“白血病”。如果求联合分布则会得到一个较小的概率值(因为得白血病的人本来就不多,加上有其他症状干扰),但是如果使用后验概率,则能排除此干扰。
1. 积化和的最大化
最大后验概率是一种推理手段。w = argmax P(W|e)。 W是尚未观测到的随机变量,使得此概率最大的意义是在获得某观测后,推断最可能发生了什么。这个公式把MAP变成了一个优化问题。P(X)实际上是一系列 P(scope)的乘积。在取对数的情况下,积就变成了和,对数的底是可以随意选择的。demo example 如下图所示.
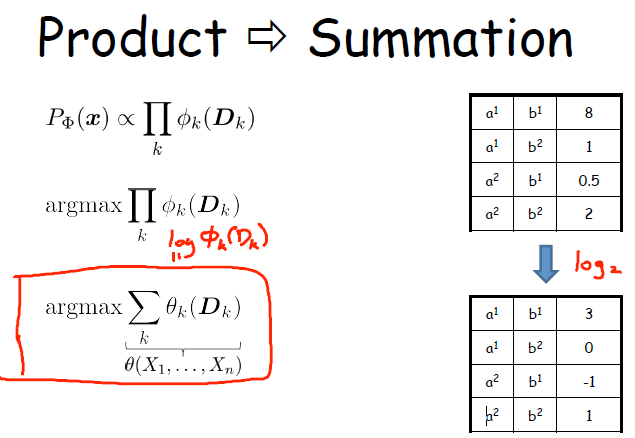
如果 PHI_k (Dk) 是链状分解的情况下,可以采用变量分离最大化的方式来求取其最大值。如图所示:

由变量边际类比可知,还可由消息传递的方式来计算最终结果。实际上这里的最大值代替了边际。利用消息传递的方式计算最大后验概率如图所示:
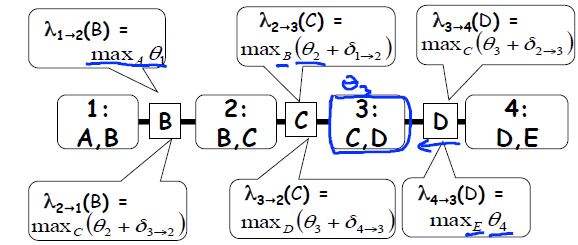
最大化执行完毕后,得到的是各个变量的“势”,以及使得“势”最大的变量组合取值。简而言之,就是一组推断的结果。
2. NP完备的MAP问题
2.1 对应问题
对应问题是在工程中经常碰到的问题。例如多目视觉中的配准,同一个物体被不同像素观测到。那么我们关心的两个不同的像素值各是多少。这个像素值本质是随机变量,物体是观测量。该问题可以直观的表示为下图:


2.2 联系势能与最小割
联系势能往往用于一种特殊的MRF中,例如 pair wise MRF(成对的马尔科夫网络)。这种网络有一个特点就是随机变量之间两两相连,随机变量(用于图像分割问题则是label,三维重构中则是深度)可以分为两个部分,第一是图的顶点,也就是图片的像素,第二是图的边,也就是两个相连像素的邻接关系(xixj)。pair wise 马尔科夫场就是这样定义变量scope的,原因不明。
针对相邻的两个变量,可以定义Phi_(xi,xj)为联系势能,其表述如下图所示。
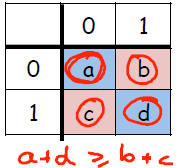
其中,a+d>b+c表示相邻的两个像素应该相近。此外再利用罚函数防止边缘误判。最后通过最小割算法对连接势能进行分割则可达成图像分割的目的。
2.3 基数因子,离散因子
因子法比较简单粗暴,直接对某种随机变量的特定组合,一般是scope的组合,定义一个因子,希望可能发生的就把因子定义的尽可能大。其中基数因子利用直接统计随机变量取值的方式,如相邻4像素均为蓝色,则label可能是天空的概率就极高。
离散因子法是针对某些特定组合定义较高的势能,而其他组合则给较低的势能,这种势能定义方法往往用于输入判断。如果输入某个拼音组合和字典中的某个词对应,则提示改词。
2.4 凸因子
凸因子是在一串随机变量中给出一个凸紧集的方式,本质上是强化目标的连续性。例如图像分割问题中,相邻像素的label极大可能是相同的。以此为约束可提高运算速度。