5.1 根据表5.1所给的训练数据集,利用信息增益比(C4.5算法)生成决策树。
注意这里是用信息增益比哦,
from sklearn.tree import DecisionTreeClassifier这里默认是gini
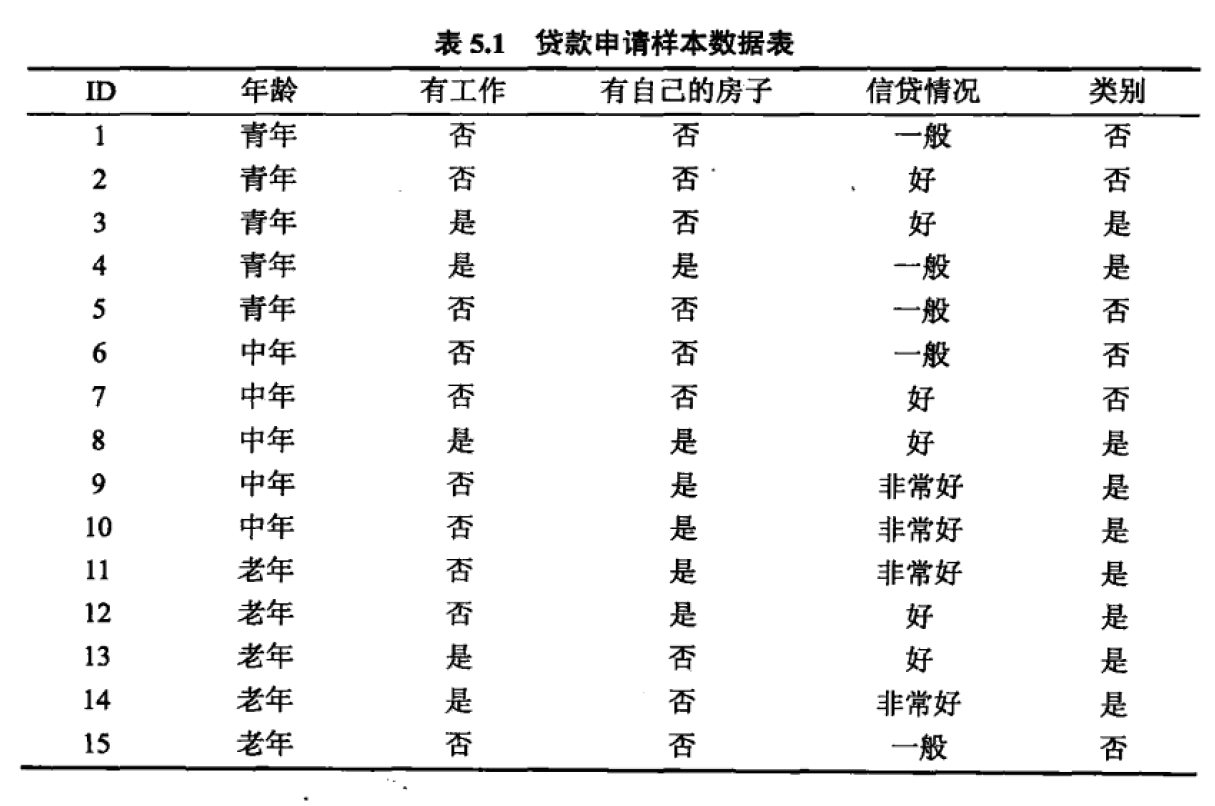
首先计算数据集(D)的经验熵(H(D)):
(H(D)=-frac{6}{15}log_2frac{6}{15}-frac{9}{15}log_2frac{9}
{15}=0.97095)
(H(D|A_1)=frac{5}{15}*(-frac{3}{5}log_2frac{3}{5}-frac{2}{5}log_2frac{2}{5})+frac{5}{15}*(-frac{3}{5}log_2frac{3}{5}-frac{2}{5}log_2frac{2}{5})+frac{5}{15}*(-frac{1}{5}log_2frac{1}{5}-frac{4}{5}log_2frac{4}{5})=0.88794)
(H(D|A_2)=frac{5}{15}*(-frac{5}{5}log_2frac{5}{5}-frac{0}{5}log_2frac{0}{5}) +frac{10}{15}*(-frac{6}{10}log_2frac{6}{10}-frac{4}{10}log_2frac{4}{10}) =0.64730)
(H(D|A_3)=frac{6}{15}*(-frac{6}{6}log_2frac{6}{6}-frac{0}{6}log_2frac{0}{6}) +frac{9}{15}*(-frac{3}{9}log_2frac{3}{9}-frac{6}{9}log_2frac{6}{9}) =0.55098)
然后计算数据集(D)关于各个特征A的值的熵(HA(D)):
(H_{A_1}(D)=-frac{5}{15}*log_2frac{5}{15}-frac{5}{15}*log_2frac{5}{15}-frac{5}{15}*log_2frac{5}{15} =1.58496)
(H_{A_2}(D)=-frac{5}{15}*log_2frac{5}{15}-frac{10}{15}*log_2frac{10}{15} =0.91830)
(H_{A_3}(D)=-frac{6}{15}*log_2frac{6}{15}-frac{9}{15}*log_2frac{9}{15} =0.97095)
(H_{A_4}(D)=-frac{5}{15}*log_2frac{5}{15}-frac{6}{15}*log_2frac{6}{15}-frac{4}{15}*log_2frac{4}{15} =1.56605)
好了,可以计算各个特征的信息增益比(g_R(D,A))了
(g_R(D,A_1)=frac{H(D)-H(D|A_1)}{H_{A_1}(D)}
=frac{0.97095-0.88794}{1.58496}
=0.05237)
(g_R(D,A_2)=frac{H(D)-H(D|A_1)}{H_{A_2}(D)} =frac{0.97095-0.64730}{0.91830} =0.35244)
(g_R(D,A_3)=frac{H(D)-H(D|A_1)}{H_{A_3}(D)} =frac{0.97095-0.55098}{0.97095} =0.43253)
(g_R(D,A_4)=frac{H(D)-H(D|A_1)}{H_{A_4}(D)} =frac{0.97095-0.60796}{1.56605} =0.23179)
选择信息增益比最大的特征(A_3),“有自己的房子”,作为分支的特征条件,把数据集(D)分为两部分(D_1(有自己的房子)),(D_2(没有自己的房子)),如下图所示:

(下面分别对数据集D_1,D_2建树,D_1,D_2上的特征有A_1,A_2,A_4. 数据集D_1中的实例都属于同一类(“是”),建立单节点数,类别为“是”; 分别计算针对数据集D_2的各个特征的信息增益比。 首先计算经验熵H(D_2))
(H(D_2)=-frac{3}{9}log_2frac{3}{9}-frac{6}{9}log_2frac{6}{9}=0.91830)
(然后计算各个特征的经验条件熵 H(D_2|A))
(H(D_2|A_1)=frac{4}{9}*(-frac{1}{4}log_2frac{1}{4}-frac{3}{4}log_2frac{3}{4}) +frac{2}{9}*(-frac{0}{2}log_2frac{02}{2}-frac{2}{2}log_2frac{2}{2}) +frac{3}{9}*(-frac{1}{3}log_2frac{1}{3}-frac{2}{3}log_2frac{2}{3})=0.66667)
(H(D_2|A_2)=frac{3}{9}*0+frac{6}{9}*0=0)
(H(D_2|A_4)=frac{4}{9}*0+frac{4}{9}*(-frac{2}{4}log_2frac{2}{4}-frac{2}{4}log_2frac{2}{4})+frac{1}{9}*0=0.44444)
(然后计算在数据集D_2中各个特征的取值的经验熵H_A(D_2):)
(H_{A_1}(D_2)=-frac{4}{9}log_2frac{4}{9}-frac{2}{9}log_2frac{2}{9}-frac{3}{9}log_2frac{3}{9}=1.53050)
(H_{A_2}(D_2)=-frac{3}{9}log_2frac{3}{9}-frac{6}{9}log_2frac{6}{9}=0.91830)
(H_{A_4}(D_2)=-frac{4}{9}log_2frac{4}{9}-frac{4}{9}log_2frac{4}{9}-frac{1}{9}log_2frac{1}{9}=1.39214)
下面计算各个特征的信息增益比:
(g_R(D_2,A_1)=frac{H(D_2)-H(D_2|A_1)}{H_{A_1}(D_2)}=frac{0.91830-0.66667}{1.53050}=0.16441)
(g_R(D_2,A_2)=frac{H(D_2)-H(D_2|A_2)}{H_{A_2}(D_2)}=frac{0.91830-0}{0.91830}=1)
(g_R(D_2,A_4)=frac{H(D_2)-H(D_2|A_4)}{H_{A_4}(D_2)}=frac{0.91830-0.44444}{1.39214}=0.34038)
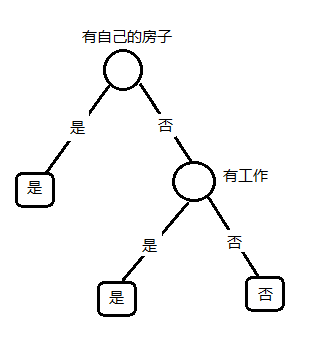
(选择信息增益比最大的特征A_2,有工作,作为分支的特征条件,将D_2划分为两部分,D_3:有工作,D_4:没有工作。如下图所示:)

(分别对数据集D_3,D_4建树,数据集的特征只有A_1,A_4:
数据集D_3中的所有实例都属于同一个类“是”,所以建立单节点树,类别为“是”;
同理数据集D_4也是单节点树,类别是“否”。
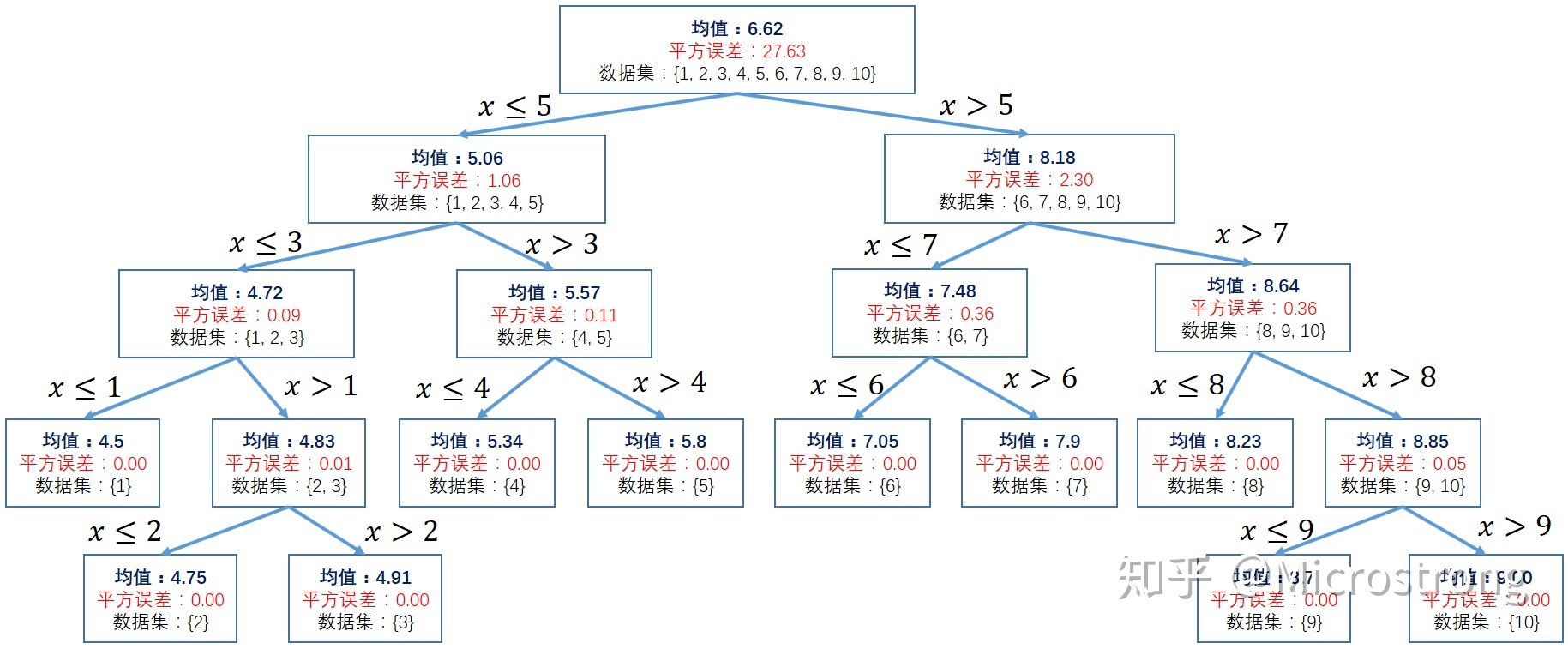
建完了,树如下:)
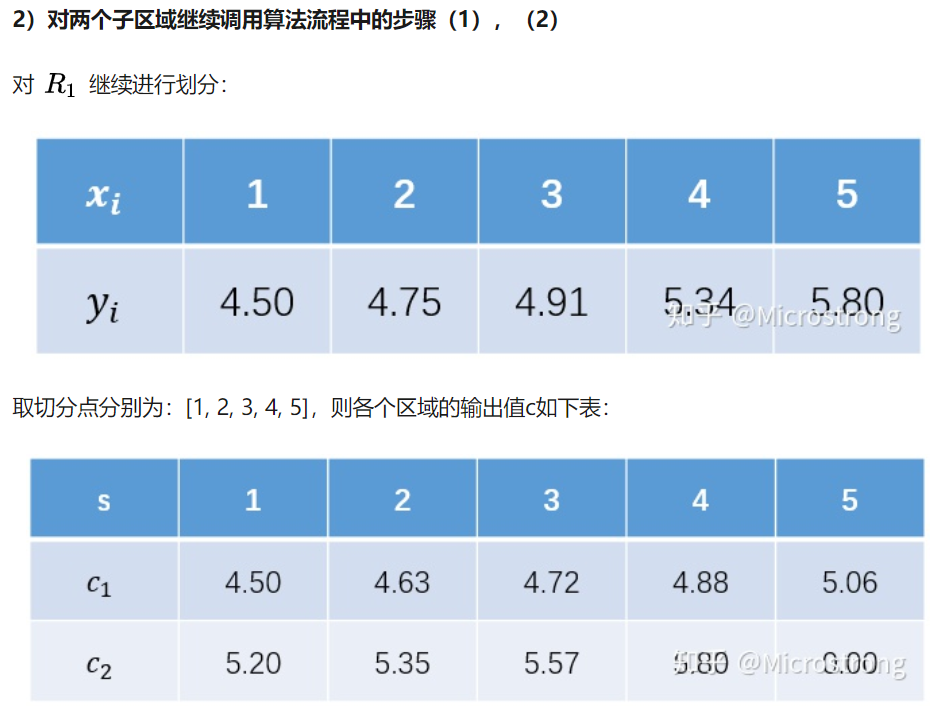
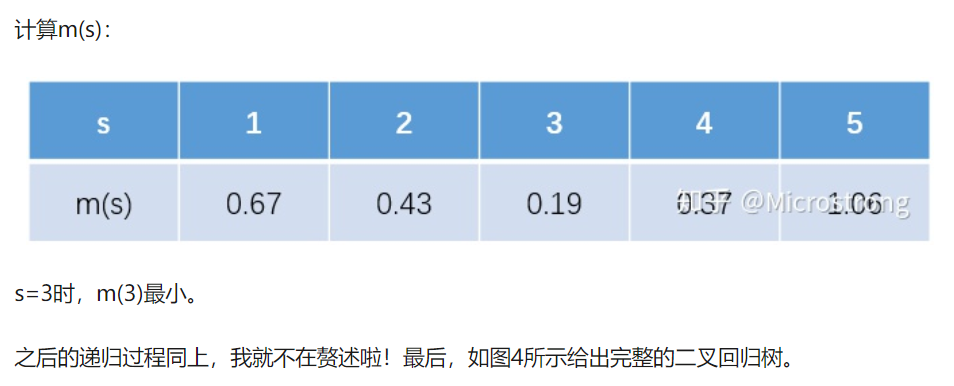
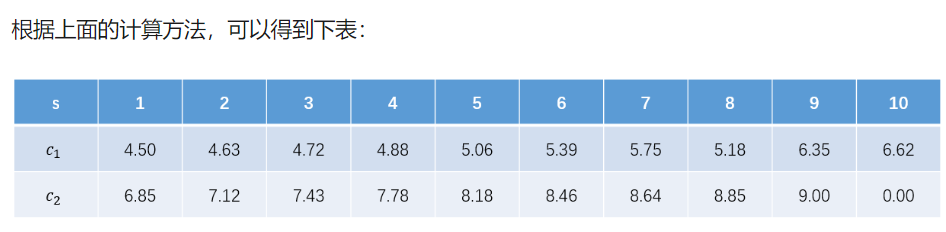
把(c_{1},c_{2})的值代入到均方差中,如下:
(m(1)=0+left{(4.75-6.85)^2+(4.91-6.85)^2+(5.34-6.85)^2+(5.80-6.85)^2+(7.05-6.85)^2+(7.90-6.85)^2+(8.23-6.85)^2+(8.70-6.85)^2+(9.00-6.85)^2
ight}=22.65)