Spark2.0机器学习系列之9： 聚类(k-means,Bisecting k-means,Streaming k-means）

在Spark2.0版本中（不是基于RDD API的MLlib），共有四种聚类方法： 
     （1）K-means 
     （2）Latent Dirichlet allocation (LDA) 
     （3）Bisecting k-means（二分k均值算法） 
     （4）Gaussian Mixture Model (GMM)。 
       基于RDD API的MLLib中，共有六种聚类方法： 
     （1）K-means 
     （2）Gaussian mixture 
     （3）Power iteration clustering (PIC) 
     （4）Latent Dirichlet allocation (LDA)
     （5）Bisecting k-means 
     （6）Streaming k-means 
       多了Power iteration clustering (PIC)和Streaming k-means两种。这些方法后面都会进行介绍。 
本文将介绍三种：K-means、Bisecting k-means与Streaming k-means。其它方法在我Spark机器学习系列里面都有介绍。

k-means

       k-means算法是最为经典的基于划分的聚类方法，是十大经典数据挖掘算法之一。K-means算法的基本思想是：以空间中k个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果。 
       假设要把样本集分为c个类别，算法描述如下： 
       （1）适当选择c个类的初始中心； 
       （2）在第k次迭代中，对任意一个样本，求其到c个中心的距离，将该样本归到距离最短的中心所在的类； 
       （3）利用均值等方法更新该类的中心值； 
       （4）对于所有的c个聚类中心，如果利用（2）（3）的迭代法更新后，值保持不变，则迭代结束，否则继续迭代。 
       该算法的最大优势在于简洁和快速。算法的关键在于初始中心的选择和距离公式。 
       Spark MLlib K-means 算法的实现在初始聚类点的选择上，借鉴了一个叫 K-means || 的类 K-means++ 实现。K-means++ 算法在初始点选择上遵循一个基本原则: 初始聚类中心点相互之间的距离应该尽可能的远。基本步骤如下: 
      第一步，从数据集 X 中随机选择一个点作为第一个初始点。 
      第二步，计算数据集中所有点与最新选择的中心点的距离 D(x)。 
      第三步，选择下一个中心点，使得 

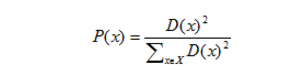最大。

  第四部，重复 (二),(三) 步过程，直到 K 个初始点选择完成。

import org.apache.spark.sql.SparkSession
import org.apache.spark.ml.clustering.KMeans
import org.apache.log4j.{Level, Logger}

object myClusters {
  def main(args:Array[String]){
    val spark=SparkSession
            .builder()
            .appName("myClusters")
            .master("local[4]")
            .config("spark.sql.warehouse.dir","/home/Spark/spark-warehouse" )
            .getOrCreate();
    val dataset=spark.read.format("libsvm")
                          .load("/home/spark-2.0.0-bin-hadoop2.6/data/mllib/sample_kmeans_data.txt")

    //屏蔽日志
    Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)

    //训练kmean模型
    val kmeans=new KMeans()
                    .setK(2)//表示期望的聚类的个数
                    .setMaxIter(100)//表示方法单次运行最大的迭代次数
                    .setSeed(1L)//集群初始化时的随机种子
    val model=kmeans.fit(dataset)

    // 评估聚类结果误差平方和（Sum of the Squared Error，简称SSE）.
    val SSE=model.computeCost(dataset)
    println(s"within set sum of squared error = $SSE")

    println("Cluster Centers: ")
    model.clusterCenters.foreach(println) 
  }  
}

如何选择K

       K 的选择是 K-means 算法的关键，computeCost 方法，该方法通过计算所有数据点到其最近的中心点的平方和来评估聚类的效果。一般来说，同样的迭代次数和算法跑的次数，这个值越小代表聚类的效果越好。但是在实际情况下，我们还要考虑到聚类结果的可解释性，不能一味的选择使 computeCost 结果值最小的那个 K。

KMeans优缺点

优点： 
      原理比较容易理解，容易实现，并且聚类效果良好，有着广泛的使用 
缺点： 
       （1）K-means算法不适用于非球形簇的聚类，而且不同尺寸和密度类型的簇，也不太适合。 
       （2）可能收敛到局部值。

Bisecting k-means（二分K均值算法）

       二分k均值（bisecting k-means）是一种层次聚类方法，算法的主要思想是：首先将所有点作为一个簇，然后将该簇一分为二。之后选择能最大程度降低聚类代价函数（也就是误差平方和）的簇划分为两个簇。以此进行下去，直到簇的数目等于用户给定的数目K为止。 
       以上隐含着一个原则是：因为聚类的误差平方和能够衡量聚类性能，该值越小表示数据点月接近于它们的质心，聚类效果就越好。所以我们就需要对误差平方和最大的簇进行再一次的划分，因为误差平方和越大，表示该簇聚类越不好，越有可能是多个簇被当成一个簇了，所以我们首先需要对这个簇进行划分。

       bisecting k-means通常比常规K-Means方法运算快一些，也和K-Means聚类方法得到结果有所不同。 
    Bisecting k-means is a kind of hierarchical clustering using a divisive (or “top-down”) approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy. 
    Bisecting K-means can often be much faster than regular K-means, but it will generally produce a different clustering. 
     二分k均值算法的伪代码如下：

将所有的点看成一个簇
当簇数目小于k时
       对每一个簇：
              计算总误差
              在给定的簇上面进行k-均值聚类k=2
              计算将该簇一分为二后的总误差
       选择使得误差最小的那个簇进行划分操作

//BisectingKMeans和K-Means API基本上是一样的，参数也是相同的
//模型训练
val bkmeans=new BisectingKMeans()
                        .setK(2)
                        .setMaxIter(100)
                        .setSeed(1L)
val model=bkmeans.fit(dataset)

//显示聚类中心    
model.clusterCenters.foreach(println)

//SSE（sum of squared error）结果评估    
val WSSSE=model.computeCost(dataset)
println(s"within set sum of squared error = $WSSSE")

Bisecting k-means优缺点 
       同k-means算法一样，Bisecting k-means算法不适用于非球形簇的聚类，而且不同尺寸和密度的类型的簇，也不太适合。

Streaming k-means 流式k-means

       Streaming k-means仍在Mllib RDD-based API中。 
       翻译参考文献（1）和（4）。 
      在streaming环境中，我们的数据是分批到来的，每一批可能包含许多点（样本）的数据。标准k-means算法在streaming环境中最简单的扩展方式是：（a)一开始以随机位置作为聚类的中心，因为这时候我们还没有看到任何的数据。(b)对于新到的每一批数据点，运用前面k-means算法中的（2）、（3）两步骤更新中心点。（c）然后我们就可以用更新后的中心点作为下一批数据更新时的初始中心点,以此反复，随着时间持续运行。 
      In the streaming setting, our data arrive in batches, with potentially many data points per batch. The simplest extension of the standard k-means algorithm would be to begin with cluster centers — usually random locations, because we haven’t yet seen any data — and for each new batch of data points, perform the same two-step operation described above. Then, we use the new centers to repeat the procedure on the next batch. Above is a movie showing the behavior of this algorithm for two-dimensional data streaming from three clusters that are slowly drifting over time. The centers track the true clusters and adapt to the changes over time. 
以一个二维特征的数据流为例，下面的动画展示了这个算法的特点，具有三个中心的数据流在随着时间缓慢漂移，计算出来的三个聚类中心也随之发生改变。 

参考文献: 
（1）Spark document 
http://spark.apache.org/docs/latest/mllib-clustering.html#streaming-k-means 
（2）Spark 实战，第 4 部分: 使用 Spark MLlib 做 K-means 聚类分析 王 龙, 软件开发工程师, IBM，写的非常详细，建议阅读。 
http://www.ibm.com/developerworks/cn/opensource/os-cn-spark-practice4/ 
（3）Bisecting k-means聚类算法实现 http://shiyanjun.cn/archives/1388.html 
（4）Introducing streaming k-means in Apache Spark 1.2 by Jeremy Freemanhttps://databricks.com/blog/2015/01/28/introducing-streaming-k-means-in-spark-1-2.html 
（5）Mahout StreamingKMeans algorithm 
http://mahout.apache.org/users/clustering/streaming-k-means.html