梯度下降算法
详细解读:https://www.jianshu.com/p/c7e642877b0e
梯度上升法VS梯度下降法:https://www.cnblogs.com/hitwhhw09/p/4715030.html
梯度下降的场景假设
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的能力。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率,来确保下山的方向不错误,同时又不至于耗时太多!
梯度下降算法是最优化中很常用的一个算法,他能找到一个局部最优解,如果目标函数是凸函数,那么他能找到全局的最优解
两个特性可以解释梯度下降法:
1:走一步看一步
2:每一步的“利益”最大化
- (一)走一步看一步
学过高数的都知道,假设我在一座山峰上,如果我想最快速下山,我选择的方向应该是梯度方向的反方向,由于山峰曲面每一点的梯度都是不一样的,所以我走一小步就要重新算一下当前的梯度,以决定下一步该往哪个方向走
- (二)每一步的“利益”最大化
现在我有了下一步的方向,还有了出发位置,剩下的就是解决这一步跨多远的问题了,我要找到一个距离,使得恰好走这么远,我的高度下降最多,走远了不行,走近了也不行
- (三)见好就收
我在当前位置,向哪个方向走,都不能再下降了,或者下降非常非常缓慢,可以认为找到一个最优点
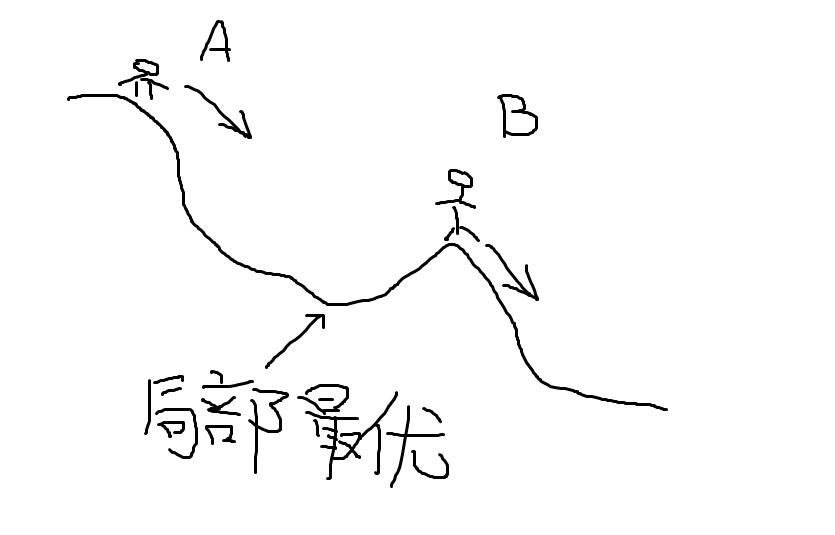
梯度上升法几何解释:
相对于梯度下降法
还有梯度上升法。(注意减号变成加号了)
其基本原理与下降法一致,区别在于:梯度上升法是求函数的局部最大值。因此,对比梯度下降法,其几何意义和很好理解,那就是:算法的迭代过程是一个“上坡”的过程,每一步选择坡度变化率最大的方向往上走,这个方向就是函数在这一点梯度方向(注意不是反方向了)。最后随着迭代的进行,梯度还是不断减小,最后趋近与零。
有一点我是这样认为的:所谓的梯度“上升”和“下降”,一方面指的是你要计算的结果是函数的极大值还是极小值。计算极小值,就用梯度下降,计算极大值,就是梯度上升;另一方面,运用上升法的时候参数是不断增加的,下降法是参数是不断减小的。但是,在这个过程中,“梯度”本身都是下降的。
最小二乘法
一元线性回归
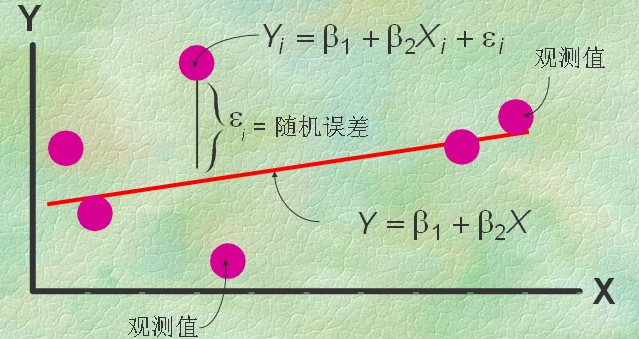
最小二乘法:如上图中屏幕上那么多红点表示为一堆X、Y值,即为{(Xi,Yi)}(i=0,1,…,m),就是要找到一条直线,较好的表达这些点的冥冥中的方向。数学上就用点到线距离的平方和累计最小来算。
这个直线的函数就称为最小二乘解,求解这个函数的解法称为最小二乘法。
样本回归模型: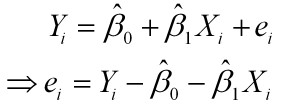
残差平方和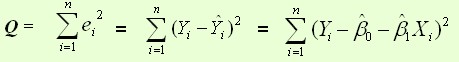
通过导数求极值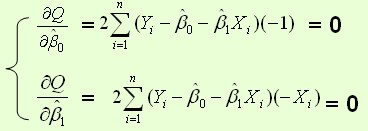
即为结果: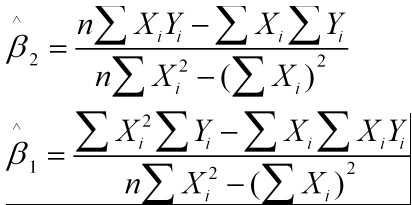
举例说明:
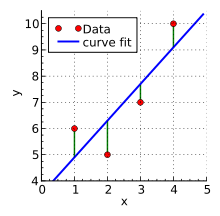
题干:有4个点(x,y):{(1,6),(2,5),(3,7),(4,10)},我们想找一条能表达这4个点的趋势的直线y=b1+b2*x,即找出在某种“较佳情况”下能够大致符合如下超定线性方程组的b1和b2:
b1+1*b2=6
b1+2*b2=5
b1+3*b2=7
b1+4*b2=10
最小二乘法采用的手段是尽量使得等号两边的方差最小,也就是找出这个函数的最小值:
S(b1,b2)=[6-(b1-1*b2)]^2+[5-(b1-2*b2)]^2+[7-(b1-3*b2)]^2+[10-(b1-4*b2)]^2
最小值可以通过对S(b1,b2)分别求b1和b2的偏导数,然后使它们等于零得到。
这个方程组只有两个未知数,容易解得:b1=3.5
b2=1.4
所以直线y=3.5+1.4x是较佳的。
线性回归问题的处理流程:
1、两个变量有关系吗?(画出散点图,直观判断)
2、这些关系可以套数学模型不?(比如或者
).
3、建立回归模型
4、对模型中参数进行估计,最小二乘法是其中一种方法。
5、讨论模型的效果咋样。
最小二乘的几何意义:
高维空间的一个向量在低维空间的投影
杂记:最小二乘估计是方差最小的无偏估计。
无偏估计
所谓总体参数估计量的无偏性指的是,基于不同的样本,使用该估计量可算出多个估计值,但它们的平均值等于被估参数的真值。
在某些场合下,无偏性的要求是有实际意义的。例如,假设在某厂商与某销售商之间存在长期的供货关系,则在对产品出厂质量检验方法的选择上,采用随机抽样的方法来估计次品率就很公平。这是因为从长期来看,这种估计方法是无偏的。比如这一次所估计出来的次品率实际上偏高,厂商吃亏了;但下一次的估计很可能偏低,厂商的损失就可以补回来。由于双方的交往会长期多次发生,这时采用无偏估计,总的来说可以达到互不吃亏的效果。
不过,在某些场合中,无偏性的要求毫无实际意义。这里又有两种情况:一种情况是在某些场合中不可能发生多次抽样。例如,假设在某厂商和某销售商之间只会发生一次买卖交易,此后不可能再发生第二次商业往来。这时双方谁也吃亏不起,这里就没有什么“平均”可言。另一种情况则是估计误差不可能相互补偿,因此“平均”不得。例如,假设需要通过试验对一个批量的某种型号导弹的系统误差做出估计。这个时候,既使我们的估计的确做到了无偏,但如果这一批导弹的系统误差实际上要么偏左,要么偏右,结果只能是大部分导弹都不能命中目标,不可能存在“偏左”与“偏右”相互抵消,从而“平均命中”的概念。
详细链接:https://www.cnblogs.com/gczr/p/8250272.html