codeforces.com/contest/810/problem/C
【题意】
给定一个集合A,求
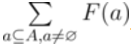 ,
,
输入:
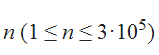
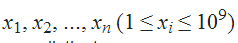
【思路】
基数为n的集合有2^n-1个非空子集。
首先n个数要从小到大排序,枚举最后的集合中最大和最小的元素是a[i]和a[j](i< j);
则f值是a[j]-a[i]的集合有2^(j-i-1)个; 然后答案+=(a[j]−a[i])*2^(j-i-1);
这样时间复杂度是O(n^2)。
我们可以把各项组合一下,把2^i提取出来。
比如考虑系数为
2^1的
必然是
a[3]-a[1]
a[4]-a[2]
a[5]-a[3]
…
a[n]-a[n-2]
=sum[n]-sum[i+1]-sum[n-i-1];
sum[i]是a[i]的前缀和。
这样对于[0,n-2]枚举2^i,时间复杂度是O(n),加上排序,总的时间复杂度是O(nlogn)
【注意】
sum[i]是取余后的结果,所以sum[n]-sum[i+1]-sum[n-i-1]可能是负数,要(+mod)%mod
【Accepted】

1 #include <iostream> 2 #include <stdio.h> 3 #include <cmath> 4 #include <vector> 5 #include <algorithm> 6 #include <set> 7 #include <map> 8 #include <queue> 9 #include <deque> 10 #include <stack> 11 #include <string> 12 #include <bitset> 13 #include <ctime> 14 #include<algorithm> 15 #include<cstring> 16 using namespace std; 17 typedef long long ll; 18 const int maxn=3e5+3; 19 const ll mod=1e9+7; 20 int a[maxn]; 21 int n; 22 ll sum[maxn]; 23 ll two[maxn]; 24 25 void Init() 26 { 27 two[0]=1; 28 for(int i=1;i<=maxn;i++) 29 { 30 two[i]=(two[i-1]*2)%mod; 31 } 32 } 33 int main() 34 { 35 Init(); 36 while(~scanf("%d",&n)) 37 { 38 memset(sum,0,sizeof(sum)); 39 for(int i=1;i<=n;i++) 40 { 41 scanf("%d",&a[i]); 42 } 43 sort(a+1,a+n+1); 44 for(int i=1;i<=n;i++) 45 { 46 47 sum[i]=(sum[i-1]+(ll)a[i])%mod; 48 } 49 ll ans=0; 50 for(int i=0;i<=n-2;i++) 51 { 52 ans=(ans+two[i]*(sum[n]-sum[n-i-1]-sum[i+1]+mod)%mod)%mod; 53 } 54 cout<<ans<<endl; 55 } 56 return 0; 57 }
