Leetcode 42 接雨水 双指针 空间换时间

地址 https://leetcode-cn.com/problems/trapping-rain-water/

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

解答

暴力遍历的时候

如果起点较低的一端 那么遇到较高的一端  就可以计算盛水体积

但是如果起点是较高的一端 就不好确定终点。

使用双指针确定盛水段落的左右断点

如果左边较低就从左边开始寻找比他等于或者大于的终点

如果右边较低就从右边开始寻找等于或者大于的终点

代码如下

class Solution {
public:
    int trap(vector<int>& height) {
        int ret = 0;
        int l =0;int r = height.size()-1;
        while(l < r){
            int mn = min(height[l],height[r]);
            if(mn == height[l]){
                l++;
                while(l<r && height[l] < mn){
                    ret += mn-height[l];
                    l++;
                }

            }else{
                r--;
                while(l<r && height[r]<mn){
                    ret += mn-height[r];
                    r--;
                }
            }            
        }

        return ret;
    }
};

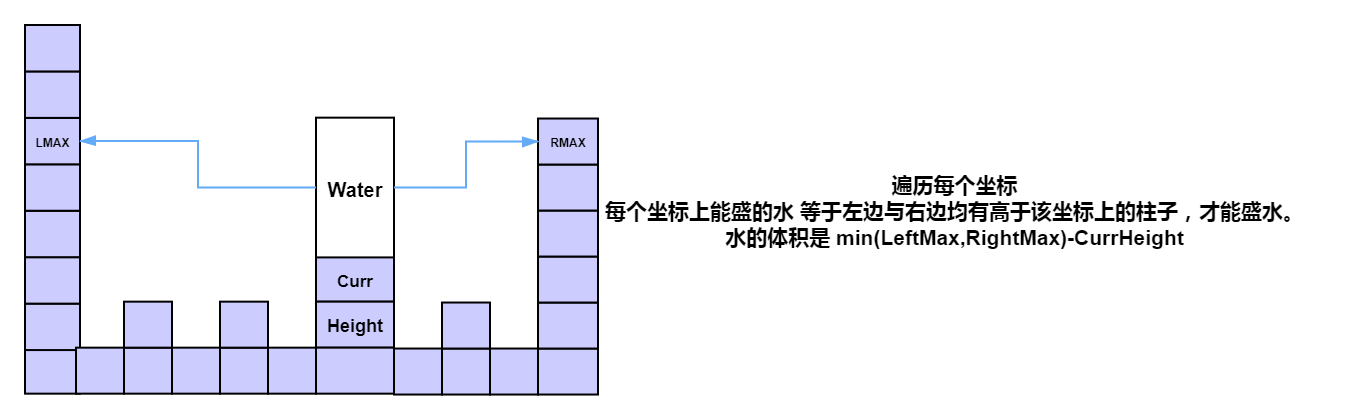
遍历每个坐标

每个坐标上能盛的水 等于左边与右边均有高于该坐标上的柱子，才能盛水。

水的体积是 min(LeftMax,RightMax)-CurrHeight

那么我们事先使用额外数组记录每个索引的左边最大高度和右边最大高度，就可以很快的得到答案。

扫描三遍  得到左边的各个最大高度值和右边的最大高度值  最后一遍计算每个索引作为U型凹陷可以盛的水的体积

复杂度是O(3n) 也就是O(n)

class Solution {
public:
    int trap(vector<int>& height) {
        height.insert(height.begin(), 0);
        height.push_back(0);

        int n = height.size();
        vector<int> leftMax(n); vector<int> rightMax(n);

        for (int i = 1; i < height.size() - 1; i++) {
            leftMax[i] = max(leftMax[i-1],height[i]);
        }

        for (int i = height.size() - 2; i >= 1; i--) {
            rightMax[i] = max(rightMax[i + 1], height[i]);
        }
        int ans = 0; 
        for (int i = 1; i < height.size() - 1; i++) {
            int val = min(leftMax[i - 1], rightMax[i + 1]) - height[i];
            if (val > 0) ans += val;
        }

        return ans;
    }
};