LeetCode 968. 监控二叉树 贪心

地址 https://leetcode-cn.com/problems/binary-tree-cameras/

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

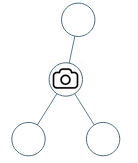
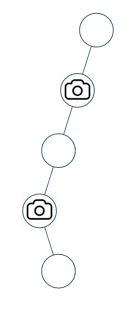
示例 2：
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

算法1
开始以为是树型DP 在考虑起始数值的时候发现要自根想叶子转移
叶子节点的状态肯定是要求被覆盖但是不会在叶子节点放置摄像机
而是在叶子节点的根上放置能够覆盖更多的点。
再列举了集中树的结构发现 均是如此，发现此题不是DP而是树的遍历和贪心

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
//1 表示已被覆盖
//2 表示需要被覆盖
//3 表示放置摄像机

int ans = 0;
int dfs(TreeNode* root)
{
    if (root == NULL) return 1;

    int l = dfs(root->left);
    int r = dfs(root->right);

    if (l == 1 && r == 1) return 2;
    if (l == 2 || r == 2) {
        ans++;
        return 3;
    }
    if( l==3 || r== 3) return 1;

    return -1;
}

int minCameraCover(TreeNode* root) {

    int r = dfs(root);
    if (r == 2) ans++;
    return ans;
}

};