剑指 Offer 36. 二叉搜索树与双向链表 树的遍历

地址  https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。
为了让您更好地理解问题，以下面的二叉搜索树为例：

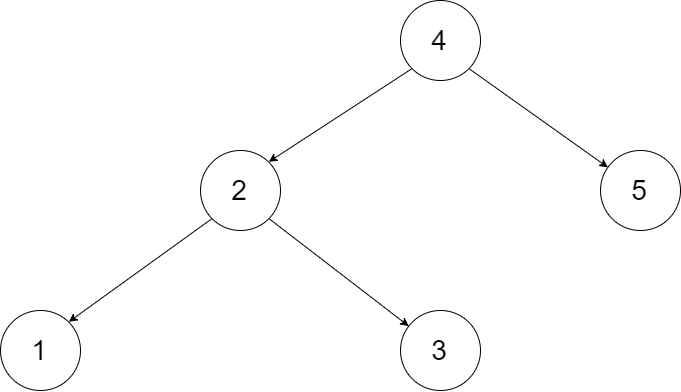
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

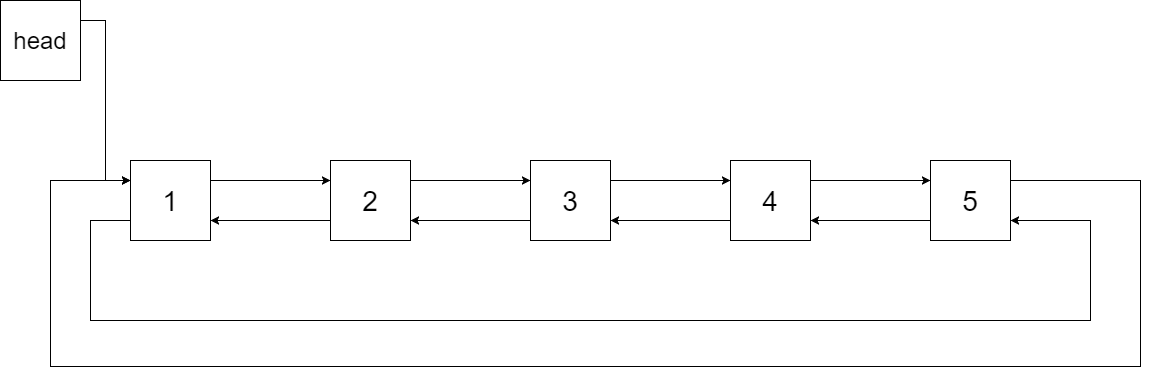
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

解答

 根据二叉搜索树的性质，转换成有序双向链表可以分为三部分，比根节点小的部分 、根节点、 比根节点大的部分

如图

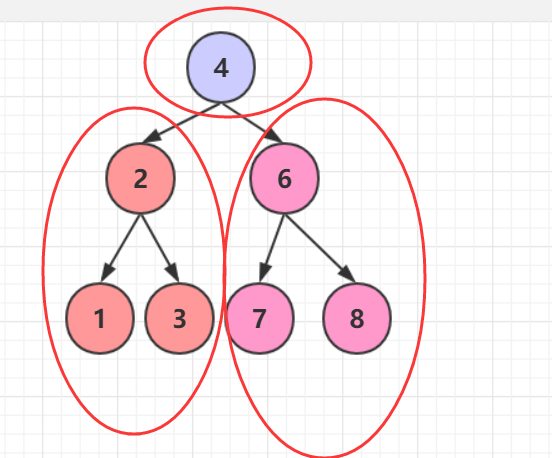
比根大的部分和比根小的部分 恰好就是缩小规模的一棵二叉搜索子树，同样是要求将一颗二叉搜索子树转化为排序双链表

这是一个很明显的递归处理模式

dfs(root->left) ; 

root连接二叉搜索左子树转化的双链表

dfs(root->right);

root连接二叉搜索右子树转化的双链表

返回左子树的链表头和 右子树的链表尾

c++代码

class Solution {
public:
    void dfs(Node* root, Node** l, Node** r) {
        Node* head = NULL;  Node* tail = NULL;
        if (root == NULL) {return;}
        *l = NULL; *r = NULL;
        dfs(root->left, l, r);
        if (*r != NULL) {
            (*r)->right = root; root->left = *r;
            head = *l;
        }
        else {
            head = root;
        }


        *l = NULL; *r = NULL;
        dfs(root->right,l,r);
        if (*l != NULL) {
            (*l)->left = root; root->right = *l;
            tail = *r;
        }
        else {
            tail = root;
        }
        *l = head; *r = tail;
        return;
    }

    Node* treeToDoublyList(Node* root) {
        if(root==NULL) return NULL;
        Node* l = NULL; Node* r = NULL;
        dfs(root,&l,&r);
        l->left = r; r->right = l;
        return l;
    }
};

STL版本 比较容易阅读 但是速度会慢一点

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
public:
    vector<Node*> dfs(Node* root){
        if(root==NULL) return vector<Node*>{NULL,NULL};
        Node* l = NULL;Node* r = NULL;
         vector<Node*> ret = dfs(root->left);
         if(ret[1]!= NULL){
            ret[1]->right=root; root->left= ret[1];
            l = ret[0];
         }else{
             l=root; 
         }

         ret = dfs(root->right);
         if(ret[1]!= NULL){
            ret[0]->left=root; root->right= ret[0];
            r = ret[1];
         }else{
             r=root; 
         }  

         return vector<Node*>{l,r};
    }

    Node* treeToDoublyList(Node* root) {
        if(root==NULL) return NULL;
        vector<Node*> v = dfs(root);
        v[0]->left = v[1]; v[1]->right=v[0];
        return v[0];
    }
};