地址 https://leetcode-cn.com/problems/gas-station/
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
如果题目有解,该答案即为唯一答案。
输入数组均为非空数组,且长度相同。
输入数组中的元素均为非负数。
示例 1:
输入:
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入:
gas = [2,3,4]
cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
解法
1 暴力
先试试暴力从每个点出法 看看能不能成功循环一周。
这里针对循环 使用了一个小技巧
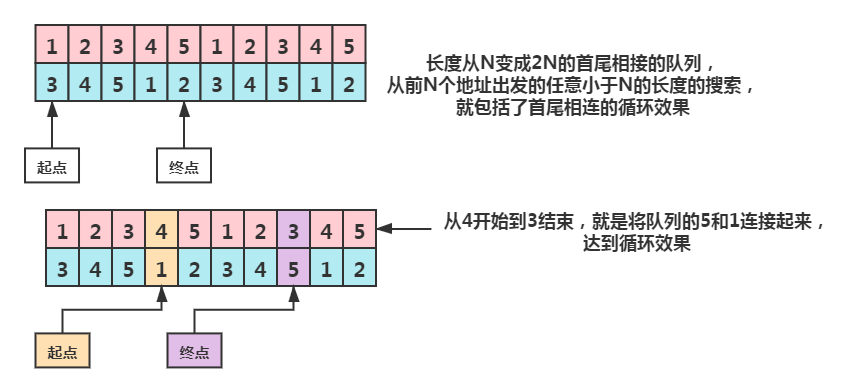
循环的队列,我们将这个队列重复两次,那么在一个队列长度内就达到了终点连接起点的循环效果
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
如图
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
gas.insert(gas.end(),gas.begin(),gas.end());
cost.insert(cost.end(),cost.begin(),cost.end());
int maxSum = -9999999;
for(int i = 0; i < gas.size()/2;i++){
//当前加油站加油行驶到下一个站 还有剩余 可以尝试
if(gas[i]-cost[i] >=0){
int startidx = i;
int sum =0; int sucess = 1;
for(int j = 0; j < gas.size()/2;j++){
sum += gas[startidx+j]-cost[startidx+j];
if(sum <0 ) {sucess = 0; break;}
}
if(sucess==1 && sum >=0){
return i;
}
}
}
return -1;
}
};

根据测试,数据量大约在10^4左右,暴力的复杂度为O(n^2),勉强能过,那么能否优化呢?
2 优化
观察规律,我们能做的优化除了上述的,选择加油量大于达到下个站点的油耗的站点作为起始点,还可以做其他优化。
如图

选择点 gas5 cost2 这个点是个很好的起点,可以加油量为5,达到下一个加油站的油耗为2,也就是说达到下一个加油站还可以剩余3单位的油。
我们观看前一个点 gas 4 cost 1 ,那么以这个点作为起点,再达到 gas5 cost2 这个点不是可以剩余更多的油吗?
也就是gas4点 作为起点最坏是和gas5作为起点的情况是持平的,而且如果cost小4的话 以gas4为起点,能剩下更多的油。
处于贪心的思考模式,如果有连续多个点都能加油大于达到下一个点的油耗,那么我们选择这多个点中的起点。
在这个图里就是选择gas4的点比gas5的点更优。
同样的,如果更优的点也无法循环一周,那么次优的点就不必尝试了。直接pass去寻找下一个不连续的 加油大于油耗的点再去尝试.
在暴力的基础上,添加了跳过连续次优点的代码,速度提升到4ms
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
gas.insert(gas.end(),gas.begin(),gas.end());
cost.insert(cost.end(),cost.begin(),cost.end());
int maxSum = -9999999;
for(int i = 0; i < gas.size()/2;i++){
//当前加油站加油行驶到下一个站 还有剩余 可以尝试
if(gas[i]-cost[i] >=0){
int startidx = i;
int sum =0; int sucess = 1; int nextIdx = i;
for(int j = 0; j < gas.size()/2;j++){
sum += gas[startidx+j]-cost[startidx+j];
if( gas[startidx+j]-cost[startidx+j] >=0) {nextIdx =startidx+j; }
if(sum <0 ) {sucess = 0; break;}
}
if(sucess==1 && sum >=0){
return i;
}
i = nextIdx;
}
}
return -1;
}
};