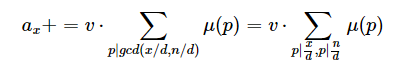设a和b的最大公约数是d,那么:
1. d是用sa+tb(s和t都是整数)能够表示的最小正整数
证明:设x=sa+tb是sa+tb能够表示出的最小正整数。首先,有d|x,证明如下:
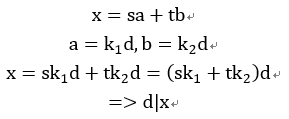
因此有x>=d,现在只要证明x是公约数,就可以证明x就是这个最大公约数了。只需证明x|a且x|b。
先证x|a。设a=qx+r(q是自然数,0<=r<x),那么r=a-qx=a-q(sa+tb)=(1-qs)a+(-qt)b。可以看出r也满足Sa+Tb这种形式,假如r也是正整数的话,r<x,那么与x是Sa+Tb这种形式的最小正整数矛盾。因此假设不成立,r不是正整数。所以r=0。所以有x|a。
证x|b同理。
所以命题得证。有结论:存在整数s,t使得sa+tb=d,其中d=gcd(a,b)。并且d是形如sa+tb的所有正整数里最小的。
2. c是a和b的公约数,那么c|d
证明:由命题1,存在整数s,t,使得sa+tb=d。由于a=pc,b=qc(p,q都是正整数),所以d=spc+tqc=(sp+tq)c。所以c|d。
所以命题得证。有结论:任何公约数都整除最大公约数。
3. 如果c|d,那么有c|a且c|b
证明:显然有d|a且d|b。由整除的传递性,就有c|a且c|b。
由命题2和命题3得出推论:一个数整除最大公约数,跟这个数分别整除这两个数是等价的条件。
这是今天在看莫比乌斯反演的时候有一步转化没有看懂,就在这里推了一下。