目录
两者所属范畴
生成模型定义
为什么叫生成模型？
判别模型定义
一个例子通俗解释两者
判别模型 VS 生成模型优缺点
参考资料
|
两者所属范畴 |
|
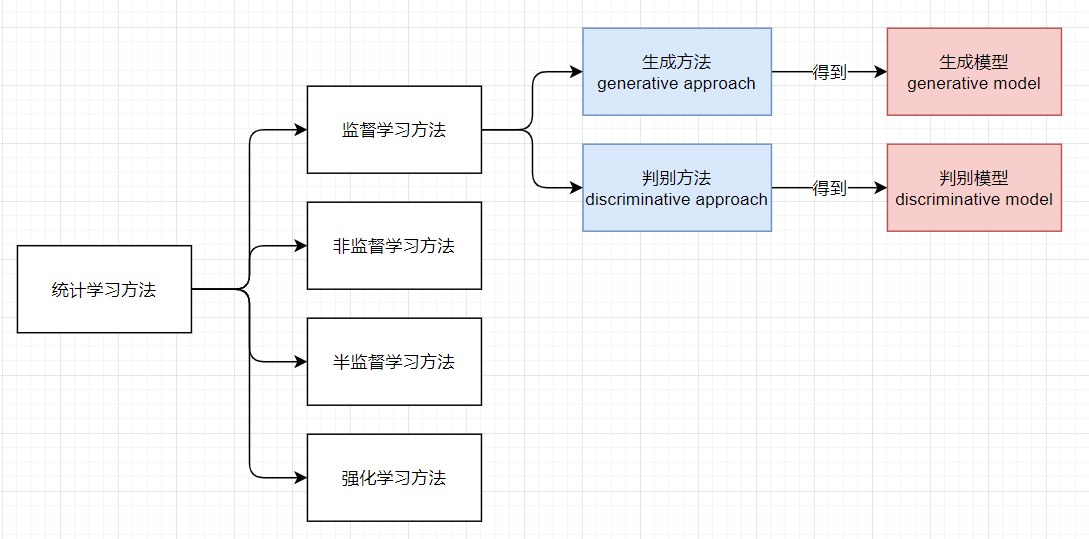
生成模型定义 |
生成方法由数据可以学习到一个联合概率分布P(X,Y)，然后通过一定方式，就可以转为一个预测模型，即生成模型：
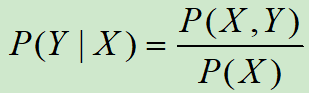
典型的生成模型有：朴素贝叶斯模型(NB)和隐马尔科夫模型(HMM)。
下面解释为什么NB模型是生成模型：
■ 由朴素贝叶斯法的定义可知：朴素贝叶斯法是通过训练数据集学习联合概率分布P(X,Y)的。
■ 根据乘法公式
可知，为了求P(X,Y)可以利用训练数据学习P(X|Y)和P(Y)。
■ 得到联合概率分布P(X,Y)后，利用贝叶斯定理，便可得到一个预测模型，即
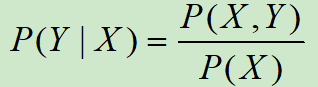
那HMM模型呢？
HMM模型是关于时序的概率模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态序列X，再由各个状态随机生成一个可观测的观测序列Y的过程。X和Y就是由一个联合概率分布P(X,Y)产生的（回忆HMM模型，
，先由π产生X1，再根据X1由B产生Y1，然后根据X1由A产生X2，最后根据X2由B产生Y2，以此类推），该联合概率分布就是HMM模型。
|
为什么叫生成模型？ |
从朴素贝叶斯模型和HMM模型可以看出，这两种模型都含有一种本领：可以表示出数据和标签共同出现的概率。因为他们中都有联合概率分布P(X,Y)，那就拥有了生成一组新的数据的能力，这个也就是名称中的生成式模型的来源。
当然，生成模型也可以做判别（预测），上一节已经阐述。顺便再说一句，判别模型只能做判别，不能生成数据。
|
判别模型定义 |
判别模型比较简单，就是由数据直接学习决策函数f(X)比如决策树，KNN等，或者直接学习条件概率分布P(Y|X)，比如逻辑回归、感知机等。
典型的判别模型有：KNN、感知机、决策树、逻辑回归、最大熵模型、SVM、提升方法和CRF等。
|
一个例子通俗解释两者 |
假设在一个大学里，有男有女，并且不同性别的人都有自己的穿衣打扮的风格。
■ 当有一个【长头发，穿短裙】的人过来的时候，生成模型和判别模型都可以对这个人的性别进行预测，并且大概率这两个模型都会将这个人预测为【女性】。这就说明了生成模型和判别模型都可以做判别（预测）。
■ 假设每一个人都是一个数据，如果想按照大学原本的分布增加一些学生的时候，生成模型可以做到，因为他深谙该大学里男女比例以及他们穿衣打扮的信息；而判别模型做不到。这就说明了生成模型掌握着整体数据的分布。
|
判别模型 VS 生成模型优缺点 |
■ 生成模型可以还原出联合概率分布，而判别模型不能。
■ 生成模型收敛速度更快。
■ 当存在隐变量时，可以使用生成模型，不能使用判别模型。
■ 生成模型在做预测的时候准确率往往较低，李航老师给出的解释是
这里从另一个角度定性来分析可以这样解释（以朴素贝叶斯为例）：
由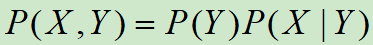
$$[sqrt {{a^2} + {b^2}} ]$$
$$[a + b = 3]$$
可以看到，相对于条件概率，在计算联合概率的时候引入了输入数据的概率分布P（X），而这并不是我们关心的（我们只关心给定X的情况下Y的分布），于是这个就相对削弱了模型的预测能力。
|
参考资料 |
《统计学习方法》李航
《深入浅出PyTorch：从模型到源码》张校捷