目录
一元线性回归、多元线性回归、Logistic回归、广义线性回归、非线性回归的关系
什么是极大似然估计
逻辑斯谛回归(Logistic回归)
多类分类Logistic回归
Python代码(sklearn库)
|
一元线性回归、多元线性回归、逻辑斯谛回归、广义线性回归、非线性回归的关系 |
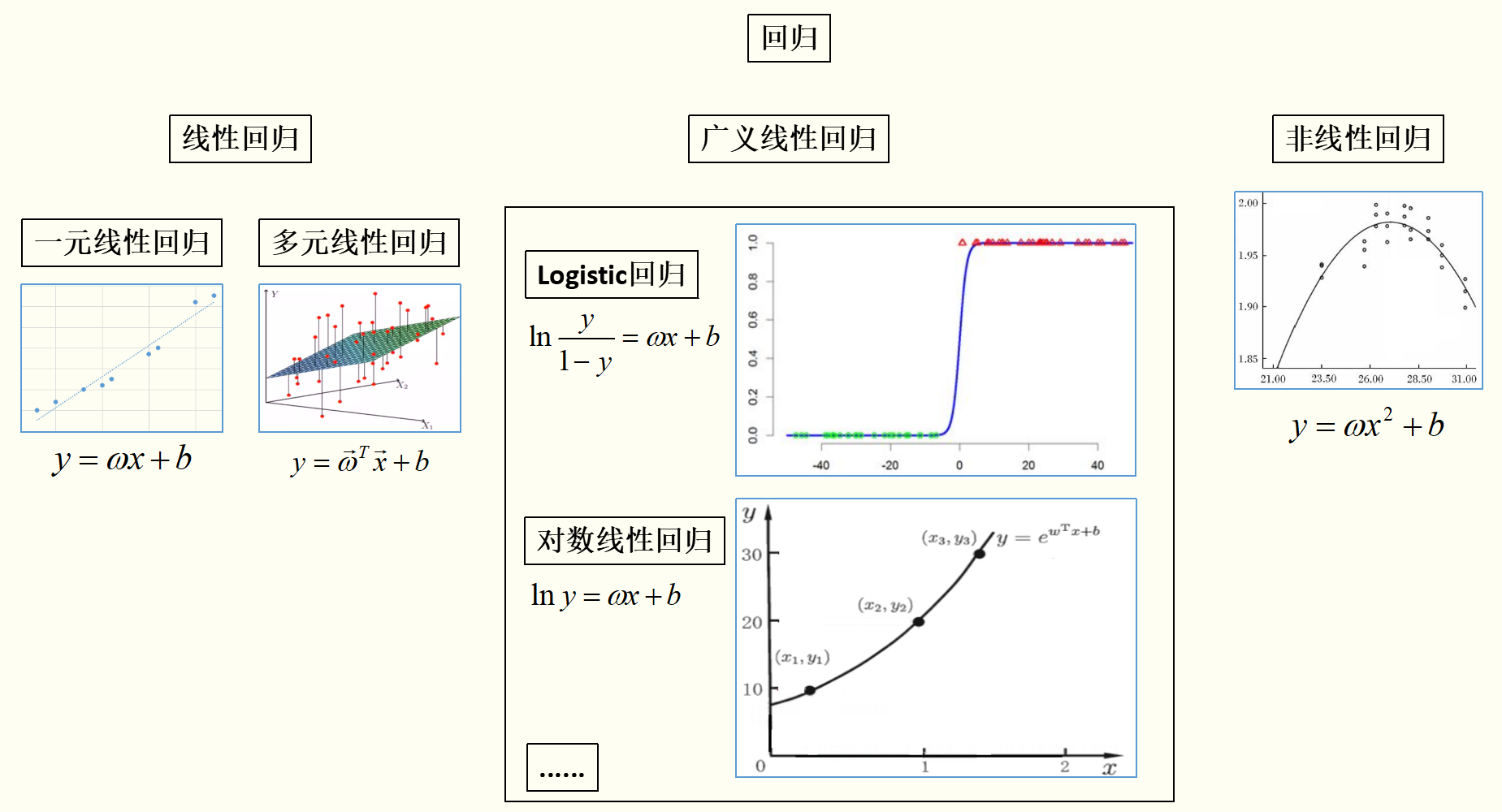
通过上图(插图摘自周志华《机器学习》及互联网)可以看出:
线性模型虽简单,却拥有着丰富的变化。例如对于样例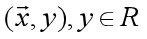 ,当我们希望线性模型的预测值逼近真实标记y时,就得到了线性回归模型:
,当我们希望线性模型的预测值逼近真实标记y时,就得到了线性回归模型: 。当令模型逼近y的衍生物,比如
。当令模型逼近y的衍生物,比如 时,就得到了对数线性回归(Log-linear regression)模型,这样的模型称为“广义线性回归(Generalized linear regression)模型”。
时,就得到了对数线性回归(Log-linear regression)模型,这样的模型称为“广义线性回归(Generalized linear regression)模型”。
|
什么是极大似然估计(Maximum Likelihood Estimate,MLE) |
引例
有两个射击运动员,一个专业水平,一个业余水平,但是不知道哪个是专业的哪个是业余的。那么如何判断呢? 让两个运动员都打几枪,A运动员平均水平9.8环,B运动员平均水平2.2环,那我们就判断了:A远动员是专业的,B运动员是业余的。因为射击成绩已经产生了9.8环,当未知参数=专业水平时,射击成绩=9.8环的概率最大。这就是极大似然法。
极大似然法:事情已经发生了,当未知参数等于多少时,能让这个事情发生的概率最大,执果索因。
百度百科定义
极大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。极大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
|
逻辑斯谛回归(Logistic回归) |
上一节讨论了如何使用线性模型进行回归学习,但若要做的是分类任务该怎么办?答案就蕴含在Logistic模型中。
在Logistic模型中,我们是用 去拟合
去拟合 ,其中y是样本x作为正例的概率。针对Logistic模型,这里有几个问题:(1)为什么要这样做拟合?(2)真实的训练集的标记都是1或0(正例或负例)而不是概率怎么办?下面我们一一解答。
,其中y是样本x作为正例的概率。针对Logistic模型,这里有几个问题:(1)为什么要这样做拟合?(2)真实的训练集的标记都是1或0(正例或负例)而不是概率怎么办?下面我们一一解答。
假设我们有训练集:

首先解释:(1)为什么要这样做拟合?
二娃:既然你的标记是概率值,是一个连续的值,是不是可以用线性模型去进行模型学习?当对新样本进行预测的时候,如果模型预测的概率值>0.5就输出1;如果模型预测的概率值<=0.5就输出0?
好,那我们就实验一下二娃提供的思路。
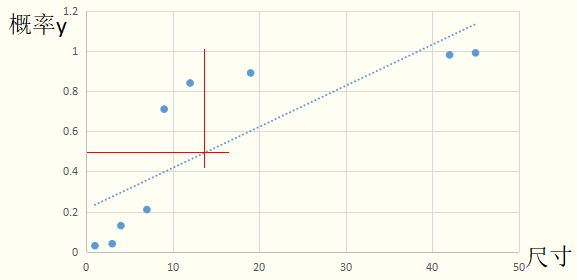
从图像上可以看出由于最后两个样本点的原因,导致我们的拟合出来的直线的斜率变小,截距变高,如果按照二娃的思路来做,模型的效果很差。所以不能用线性模型去直接拟合概率值y。
翠花:那我们为何不直接找一条分割线去分割,而是非要去拟合呢?在本例中,直接用“尺寸如果>5.5输出1,尺寸<=5.5输出0”的规则岂不是很好?
其实,翠花的思路是我们未来要讲的支持向量机(SVM)。但是当样本量较大时SVM的收敛速度很慢,所以SVM从2012年开始渐渐退出历史舞台。在用于分类的模型有很多,这里我们先介绍Logistic模型。
我们接着说二娃的问题。线性模型直接拟合概率值y的方法不好用,那么去拟合 (正例概率/反例概率,称为几率,再取对数,称为对数几率),当对新样本进行预测的时候,如果模型预测值>0就输出1;如果模型预测值<=0就输出0呢?
(正例概率/反例概率,称为几率,再取对数,称为对数几率),当对新样本进行预测的时候,如果模型预测值>0就输出1;如果模型预测值<=0就输出0呢?
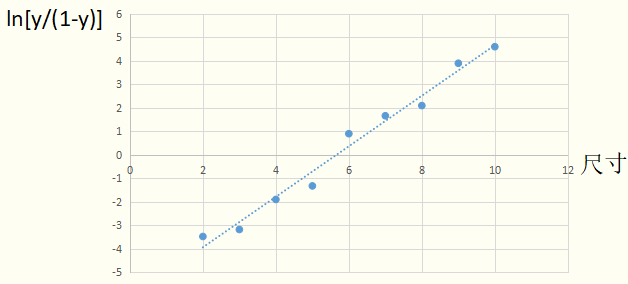
很明显,从图像拟合的情况看,模型在训练集上的表现很好。
那为什么要这样做拟合呢?首先,Logistic模型公式为: ,转换形式后:
,转换形式后: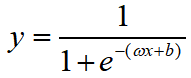 ,我们来讨论一下函数
,我们来讨论一下函数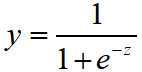 (一种Sigmoid函数)的性质
(一种Sigmoid函数)的性质
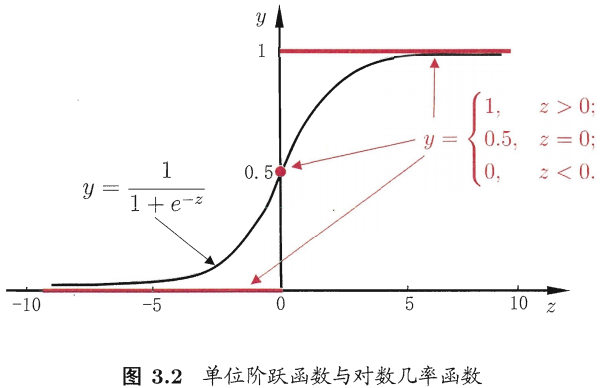 图摘自自周志华《机器学习》
图摘自自周志华《机器学习》
函数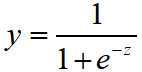 是一个单调可微函数,当z趋于正无穷时,函数值趋于1;当z趋于负无穷时,函数值趋于0;而且关于点(0,1/2)中心对称。这种Sigmoid函数适合拟合概率值。可以粗略的画出拟合曲线:
是一个单调可微函数,当z趋于正无穷时,函数值趋于1;当z趋于负无穷时,函数值趋于0;而且关于点(0,1/2)中心对称。这种Sigmoid函数适合拟合概率值。可以粗略的画出拟合曲线:
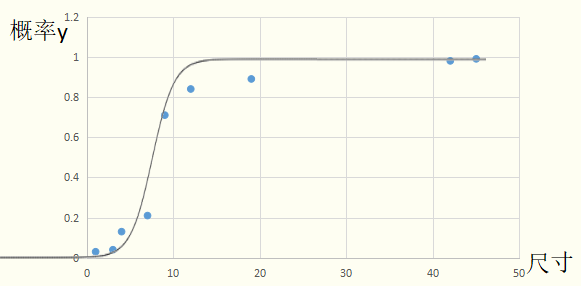
因此,当有新的样本输入时,Logistic回归模型中的函数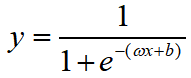 会计算出它是正例的概率。若y>0.5模型预测为1(是恶性肿瘤),否则为0(非恶性肿瘤)。
会计算出它是正例的概率。若y>0.5模型预测为1(是恶性肿瘤),否则为0(非恶性肿瘤)。
随后解释:(2)真实的训练集的标记都是1或0(正例或负例)而不是概率怎么办?
假设数据集为

我们知道函数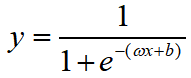 可以表示某个样例是正例的概率。虽然其中的
可以表示某个样例是正例的概率。虽然其中的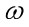 和
和 是未知的,是未知参数,但是可以表示出每一个样例属于其标记的概率,如:
是未知的,是未知参数,但是可以表示出每一个样例属于其标记的概率,如:
 ,
,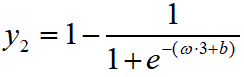 ,......,
,......,
现在有了每一个样例属于其标记的概率,然后将这些概率相乘求一个总体概率S,即:
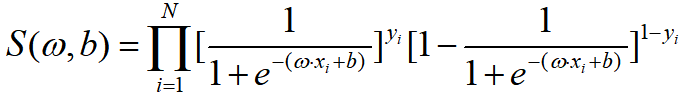 (似然函数)
(似然函数)
可以证明这个似然函数是一个凸函数,使用最优化方法令其最大,从而求出最优的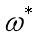 和
和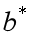 ,然后代入
,然后代入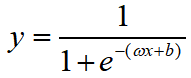 ,完成模型的求解。
,完成模型的求解。
细心的朋友一定会发现:“事情已经发生了(训练集确定了),当未知参数(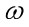 和
和 )等于多少时,能让这个事情发生的概率(S)最大,执果索因”。这正是极大似然估计的应用啊!
)等于多少时,能让这个事情发生的概率(S)最大,执果索因”。这正是极大似然估计的应用啊!
因此Logistic回归模型中学习的代价函数可以是:
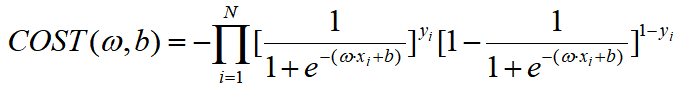
当然,我们也能求一下对数似然函数:
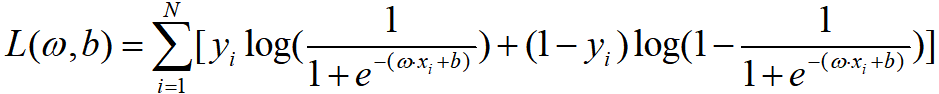
损失函数也相应变为:
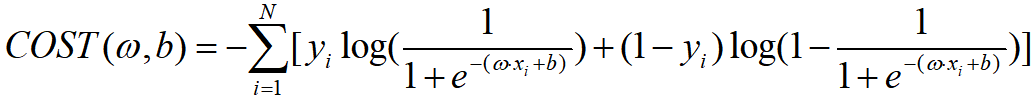
|
多类分类Logistic回归 |
有两种方式:
(1)采用one-vs-rest策略
(2)采用多分类逻辑回归策略
设离散型随机变量Y的取值集合是{1,2,...,K},那么多分类逻辑回归模型是
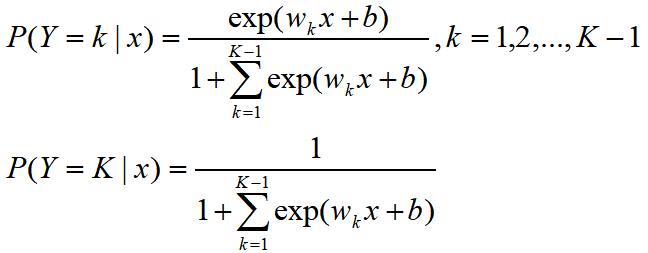
二分类逻辑回归的参数估计方法也可以推广到多分类逻辑回归。
|
Python代码(sklearn库) |
# -*- coding: utf-8 -*- from numpy import * from sklearn.datasets import load_iris from sklearn.linear_model import LogisticRegression iris = load_iris() trainX = iris.data trainY = iris.target clf = LogisticRegression(penalty='l2', dual=False, tol=1e-4, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1) ''' @param penalty: 指定正则化策略 @param dual: 是否求解对偶形式 @param C: 惩罚项系数的倒数,越大,正则化项越小 @param fit_intercept: 是否拟合截距 @param intercept_scaling: 当solver='liblinear'、fit_intercept=True时,会制造出一个恒为1的特征,权重为b,为了降低这个人造特征对正则化的影响,可以将其设为1 @param class_weight: 可以是一个字典或'balanced'。字典:可以指定每一个分类的权重;'balanced':可以指定每个分类的权重与该分类在训练集中的频率成反比 @param max_iter: 最大迭代次数 @param random_state: 一个整数或一个RandomState对象或None @param solver: 指定求解最优化问题的算法: 'newton-cg':牛顿法; 'lbfgs':拟牛顿法; 'liblinear':使用liblinear;(适用于小数据集) 'sag':使用Stochastic Average Gradient Descent算法(适用于大数据集) @param tol: 指定迭代收敛与否的阈值 @param multi_class: 'ovr': 采用one-vs-rest策略 'multi_class': 采用多类分类Logistic回归 @param verbose: 是否开启迭代过程中输出日志 @param warm_start: 是否使用前一次的训练结果继续训练 @param n_jobs: 任务并行时指定使用的CPU数,-1表示使用所有可用的CPU @attribute coef_: 权重向量 @attribute intercept_: 截距b @attribute n_iter_: 实际迭代次数 @method fit(X,y[,sample_weight]): 训练模型 @method predict(X): 预测 @method predict_log_proba(X): 返回X预测为各类别的概率的对数 @method predict_proba(X): 返回X预测为各类别的概率 @method score(X,y[,sample_weight]): 计算在(X,y)上的预测的准确率 ''' clf.fit(trainX, trainY) print "权值:"+str(clf.coef_) print "截距:"+str(clf.intercept_) print "分数:"+str(clf.score(trainX, trainY)) print clf.predict(trainX) print trainY ''' C:Anaconda2libsite-packagessklearndatasets 权值:[[ 0.41498833 1.46129739 -2.26214118 -1.0290951 ] [ 0.41663969 -1.60083319 0.57765763 -1.38553843] [-1.70752515 -1.53426834 2.47097168 2.55538211]] 截距:[ 0.26560617 1.08542374 -1.21471458] 分数:0.96 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] '''