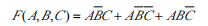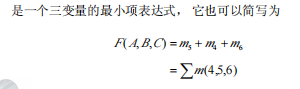2.1 逻辑代数的三种基本运算
1. 与运算(逻辑乘)
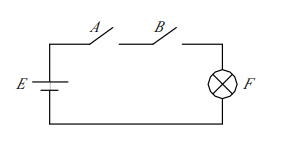
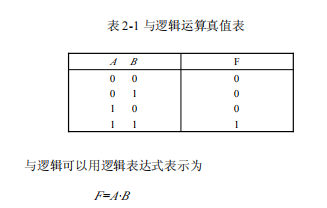
A 和 B开关都闭合(都为1) F才能亮(为1)

设二极管为理想开关,AB都通的时候,F为0
2. 或运算(逻辑加)
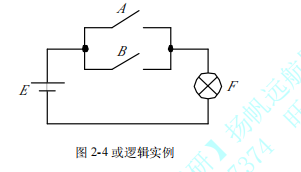
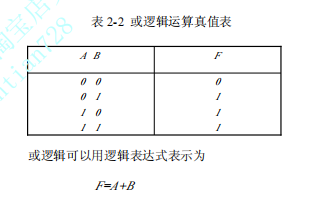
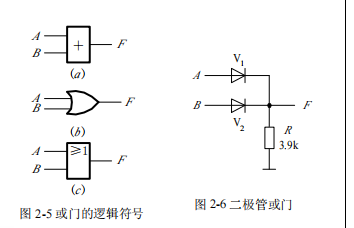
AB 有一个二极管为1 F就会为1,因为地有一个电阻。
3. 非运算(逻辑反)
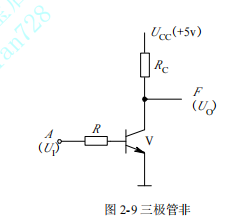
设三极管为理想,A 接通,电压从RC直接到了发射端,F是三极管集电极和发射的压降,则F为0
2.2 逻辑代数的基本定律和规则
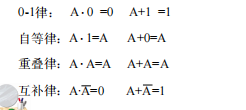

以上可以通过真值表看出。 可以通过真值表或者推算出
(A + B)(A + C)
=A+ AC + BA + BC 【AA=A 此处消掉一个A】
=A( 1+ B + C) +BC
=A + BC
3. 逻辑代数中的特殊定律
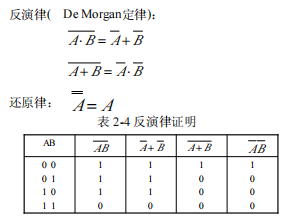
2.2.2三个重要规则
已知A+B=A·B(反演律),若用F=B+C代替等式中的B,则可以得到适用于多变量的反演律, 即(这个上横线我找了方法不知道怎么解决.....只能截图了)

2. 反演规则

3. 对偶规则


A(B + C) 对偶 A + BC
AB + BC 对偶 (A + B)(B + C) (加括号是因为原表达式AB BC的优先级高)
2.2.3 若干常用公式
合并律

B非 + B 肯定为1 A(B + B非) = A
2. 吸收律
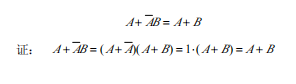
A + A'B = (A + A')(A + B) = 1(A + B)
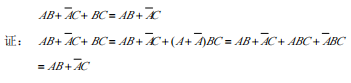
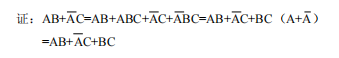
BC中缺A 缺啥补啥保证结果不变就行 两两合并 合并律 AB->AB + ABC = AB(1 + C)
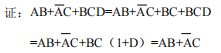
=AB + A'C + BC(A + A')
= AB + ABC + A'C + A'BC --> AB + A'C
2.3 复合逻辑

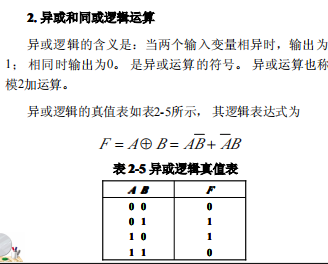
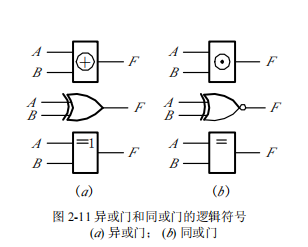

异或取非就是同或





或与 (A' + B)(A + C) = A'A + A’C + AB + BC = 0 + AB + A'C 根据吸收律 BC被省去
与非与非 把与或AB AC'分别看成一个整体 F取两次非【与非与非只有与或中间的或变成与】
F' = (AB + A'C)' 反演
= ((A '+ B ')' . (A + C')')'
或非或非 把或与 (A' + B) (A + C) 分别看成一个整体
F' = ((A' + B)(A + C))'
= ((A' + B)' + (A + C)')'
与或非 或与范燕而来
F' = ((A' + B)(A + C) ) '
(AB' + A'C')'
与或 -> 与非
或与 -> 或非
或与 -> 与或非
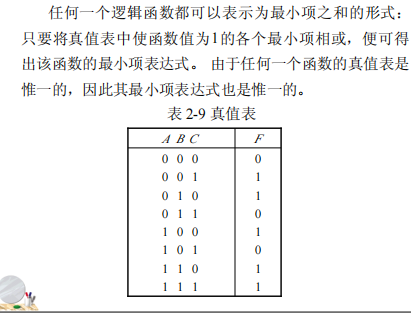
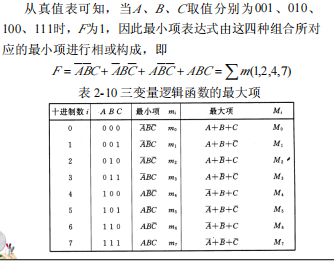
2.4 逻辑函数的两种标准形式