前言
因为实验需要用到拉普拉斯形变,但找了好久找到一个非常适合入门的资料。再此记录下我的学习过程,也算搬运翻译过来。
Introduction / Basic Laplacian Mesh Representation
首先本文的代码中的拉普拉斯形变是作用在三角网格组成的3D model上的。一个三维模型是由很多个三角网格组成,每个三角网格有三个顶点。
拉普拉斯网格通过跟踪微分顶点信息而不是绝对信息来存储三角形网格的几何信息。当在网格上执行某些变换(尤其是变形)时,它可以有效地保存顶点间的关系。它还允许以非常自然的方式在整个表面上进行平滑的插值。
所以拉普拉斯形变,最重要的就是保存了顶点间的关系。当我们移动一个点后,其他的顶点为了维持一个能量函数不变,从而跟着移动。
Laplacian 的主要思想是:
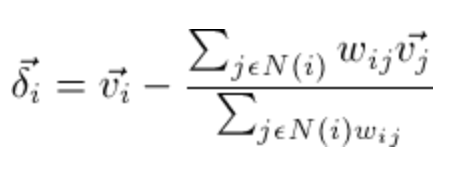
N(i)表示i的邻居,(w_{ij})就是各种权(重需要计算)。注意后面那个分式的的分母就是所有权重之和。如果i的相邻顶点的权重全部是1,那么:

这里的d_i表示i的邻居个数。这种权重全为1的情况也叫做umberalla weighting。加入有5个邻接顶点,每个都是1/5。这是什么,这就是这5个顶点组成的几何体的中心。
另外一种比较常见的权重是余切权重:

参考这幅图,选择的权重与角的余切值有关。点i和j相连的边所对的两个角的余切值组成权重:
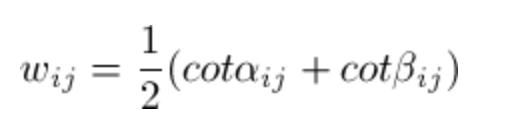
这样的给邻接点赋值权重,能更好的保存它的几何信息。
构造delta坐标系
然后构造delta坐标系,也就是记录每个点i与所有点关系的一个权重矩阵:
- 如果j是i的邻居,那么让矩阵[i,j]处的值等于(-w_{ij}),这里的(w_{ij})就是我们上面说的那些不同的权重算法,任选一种。这里选余切重。
- 如果j不是i的邻居且j不是i,那么令矩阵[i,j]处的值为0。
- 如果j==i,那么令矩阵[i,j]处的值为1。
简言之,邻接点赋值为(w_{ij}),i点处赋值为1,其他非邻接赋值为0。