1、元算法(集成算法)
元算法就是对其他算法进行组合的一种方式。也称为集成算法(ensemble method)，例如bagging方法和boosting方法。它可以是不同算法的集成；也可以是同一算法在不同设置下的集成；还可以是数据集不同部分分配给不同分类器之后的集成。
2、bagging和boosting
（1）、bagging
自举汇聚法（bootstrap aggregating），也成为bagging方法。
其是从原始数据选择S次后得到S个新数据集的一种技术，新数据集和原始数据集大小相等。（每个数据集都是从原始集合中随机选择一个样本，然后随机选择另一个样本来替换它。有的书中，也认为是放回取样得到的——比如要得到一个大小为n的数据集，该数据集的每个样本都是在原始数据集中随机抽样得到的。因此，新的数据集可能有重复的样本，原始数据集中的某些样本也可能不在新的数据集中。）
在S个数据集建好后，将某个学习算法分别作用于每个数据集得到S个分类器。对新数据分类时，选择分类器投票结果中最多的类别作为最后的分类结果。
（2）、boosting
Boosting和bagging类似，但是boosting通过串行训练获得不同的分类器，每个分类器根据已训练出的分类器的性能进行训练，集中关注被已有分类器错分的数据。
而且，boosting分类结果是基于所有分类器的加权求和得到的，每个分类器的权重不相等（bagging中分类器权重相等），每个权重代表对应分类器在上一轮迭代的成功度。
其中，AdaBoost是其中较为流行的版本。
3、AdaBoost
1、训练方法
AdaBoost是adaptive boosting（自适应boosting）的缩写。
其过程如下：
①对训练数据中的每个样本赋予一个权重，这些权重构成向量D。一开始，这些权重都相等。
②首先在训练数据上训练出一个弱分类器，并计算该分类器的错误率ε：
并为该分类器分配权重α：
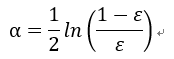
③对该分类器进行二次训练，重新调整每个样本的权重，第一次分对的样本权重会降低:
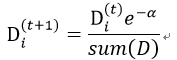
第一次分错的样本的权重会提高:
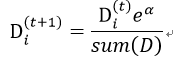
④进入下一轮迭代，训练新的弱分类器。
⑤直至 为0或者弱分类器数目达到指定值。
2、基于单层决策树实现
单层决策树仅基于单个特征进行决策。通过使用多棵单层决策树，就可以构造对数据集正确分类的多个弱分类器。
1、单层决策树确定
设最小错误率为ε=INF，数据集的样本个数为m，每个样本的特征个数为n，当前各个样本的权重列向量为D。
①第一层循环：遍历各个特征，设当前特征为i
②第二层循环：得到该特征取值的最小值min和最大值max，设最大步长stepsize，得到步长数steps，遍历步长从-1到steps，设当前步长为j：
③第三层循环：得到当前阈值min+j*stepsize，第一种情况设大于等于阈值的样本为1类；第二种情况设小于阈值的样本为1类，其余为-1类。
④循环节：得到当前分类下分错的样本，此处基于权重向量D，得到分错样本的权重和Ecur，来评价分类器。若Ecur<ε，则更新最佳分类器和错误率。
⑤遍历结束后，得到最低错误率下分类的特征、阈值、分类不等号方向。
2、训练过程
①初始化，设D为全1/m列向量。同时设置m维的全0列向量classEst，记录每个样本的累计类别估计值。设置最大迭代次数。
②对每次迭代，找到当前情况下的最佳单层决策树及其最低错误率和类别向量cls。
③通过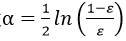
为该分类器分配权重α
④通过α调整样本权重向量D:classEst+=α*cls
⑤根据classEst的正负得到当前分类错误率，若为0，则退出迭代。
3、测试过程
①得到测试数据在各个分类器的预测结果（1类或-1类），乘以相应分类器的权重并求和，便得到每个测试样本的分类结果，根据其正负判断最后为1类还是-1类。