模板参考:https://blog.csdn.net/saramanda/article/details/55253627
综合各位大大博客后整理的模板:

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 const int maxn = 10000 + 10; 5 struct LCT 6 { 7 struct node 8 { 9 int fa, ch[2]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子 10 int reverse;//区间反转标记 11 bool is_root; //是否是所在Splay的根 12 int siz; 13 }Tree[maxn]; 14 int n; 15 16 void init(int MN) 17 { 18 for (int i = 1; i <= MN; i++) 19 { 20 Tree[i].reverse = Tree[i].fa = Tree[i].ch[0] = Tree[i].ch[1] = 0; 21 Tree[i].is_root = true; 22 Tree[i].siz = 1; 23 24 } 25 } 26 27 bool getson(int x) 28 {//x是否为重儿子 29 return x == Tree[Tree[x].fa].ch[1]; 30 } 31 bool isroot(int x) 32 { 33 return Tree[Tree[x].fa].ch[0] != x && Tree[Tree[x].fa].ch[1] != x; 34 } 35 void pushreverse(int x) 36 { 37 if (!x)return; 38 swap(Tree[x].ch[0], Tree[x].ch[1]); 39 Tree[x].reverse ^= 1; 40 } 41 void pushdown(int x) 42 {//下传反转标记 43 if (Tree[x].reverse) 44 { 45 pushreverse(Tree[x].ch[0]); 46 pushreverse(Tree[x].ch[1]); 47 Tree[x].reverse = 0; 48 } 49 } 50 51 void update(int x) 52 { 53 int l = Tree[x].ch[0], r = Tree[x].ch[1]; 54 Tree[x].siz = 1; 55 if (l) Tree[x].siz += Tree[l].siz; 56 if (r) Tree[x].siz += Tree[r].siz; 57 } 58 59 void rotate(int x) 60 {//将x旋转为根 61 if (Tree[x].is_root)return; 62 int k = getson(x), fa = Tree[x].fa; 63 int fafa = Tree[fa].fa; 64 pushdown(fa); pushdown(x); //先要下传标记 65 Tree[fa].ch[k] = Tree[x].ch[k ^ 1]; 66 if (Tree[x].ch[k ^ 1])Tree[Tree[x].ch[k ^ 1]].fa = fa; 67 Tree[x].ch[k ^ 1] = fa; 68 Tree[fa].fa = x; 69 Tree[x].fa = fafa; 70 if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[1]] = x; 71 else Tree[x].is_root = true, Tree[fa].is_root = false; 72 update(fa);update(x); //如果维护了信息,就要更新节点 73 } 74 void push(int x) 75 { 76 if (!Tree[x].is_root) push(Tree[x].fa); 77 pushdown(x); 78 } 79 int findroot(int x) 80 {//找到x在原树中的根节点 81 access(x); Splay(x); 82 pushdown(x); 83 while (Tree[x].ch[0]) pushdown(x = Tree[x].ch[0]);//找到深度最小的点即为根节点 84 return x; 85 } 86 void Splay(int x) 87 {//让x成为Splay的根,且x不含右儿子 88 push(x); //在Splay到根之前,必须先传完反转标记 89 for (int fa; !Tree[x].is_root; rotate(x)) { 90 if (!Tree[fa = Tree[x].fa].is_root) { 91 rotate((getson(x) == getson(fa)) ? fa : x); 92 } 93 } 94 } 95 void access(int x) 96 {//访问某节点。作用是:对于访问的节点x,打通一条从树根(真实的LCT树)到x的重链;如果x往下是重链,那么把x往下的重边改成轻边。结束后x没有右儿子(没有深度比他大的点) 97 int y = 0; 98 do { 99 Splay(x); 100 Tree[Tree[x].ch[1]].is_root = true; 101 Tree[Tree[x].ch[1] = y].is_root = false; 102 update(x); //如果维护了信息记得更新。 103 x = Tree[y = x].fa; 104 } while (x); 105 } 106 void mroot(int x) 107 {//把某个节点变成树根(这里的根指的是整棵LCT的根) 108 access(x);//使x与根结点处在同一棵splay中 109 Splay(x);//x成为这棵splay的根,x只有左儿子 110 //由于根节点所在的splay中,根节点没有左儿子(没有深度比他小的节点),将x的左右子树翻转 111 pushreverse(x); 112 } 113 void link(int u, int v) 114 {//连接u所在的LCT和v所在的LCT 115 mroot(u);//先让u成为其所在LCT的根 116 if(findroot(v)!=u)Tree[u].fa = v;//如果u与v不在同一棵splay中,就把v设置为u的父亲 117 } 118 void cut(int u, int v) 119 {//分离出两棵LCT 120 mroot(u); //先让u成为其所在LCT的根 121 access(v); //让u和v在同一棵Splay中 122 Splay(v); //连接u、v,u是v的左儿子 123 pushdown(v); //先下传标记 124 if (Tree[v].ch[0]) 125 { 126 Tree[Tree[v].ch[0]].fa = Tree[v].fa; 127 Tree[Tree[v].ch[0]].is_root = true; 128 } 129 Tree[v].fa = 0; Tree[v].ch[0] = 0; 130 //v的左孩子表示v上方相连的重链 131 update(v); //记得维护信息 132 } 133 134 bool judge(int u, int v) 135 {//判断u和v是否连通 136 while (Tree[u].fa) u = Tree[u].fa; 137 while (Tree[v].fa) v = Tree[v].fa; 138 return u == v; 139 } 140 void split(int u, int v) 141 {//获取u->v的路径 142 mroot(u);//让u成为根结点 143 access(v);//访问v 144 Splay(v);//把v转到根结点,此时u的父亲为v 145 } 146 int Query_deep(int x) 147 {//询问x到LCT根的距离(深度) 148 access(x); 149 Splay(x); 150 return Tree[x].siz; 151 } 152 153 void modify(int x,int v) 154 {//改变点值 155 access(x); 156 Splay(x); 157 //Tree[x].val = v;更改值 158 update(x); 159 160 } 161 162 }lct; 163 int main() 164 { 165 166 return 0; 167 }
几个知识点:
1、LCT中用Splay维护链,这些Splay叫做“辅助树“。辅助树以它上面每个节点的深度为关键字维护,就是辅助树中每个节点左儿子的深度小于当前节点的深度,当前节点的深度小于右儿子的深度。
2、LCT相当于多棵splay被虚线连在一起,即splay森林;而最开始的时候是N个单独的点与他的父亲用虚线相连,每个点是一棵splay。
3、无论树怎样旋转,怎样变换,读入时所连接(link)的边(没有被cut的),一直都连着的
4、在每棵splay中每一个结点左子树中的节点都是他在原树中的祖先,右子树中的结点都是他在原树中的孩子。
5、splay森林实例:
原树:
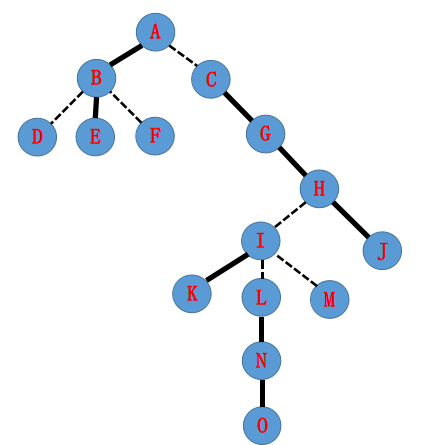
一种可能的splay森林:
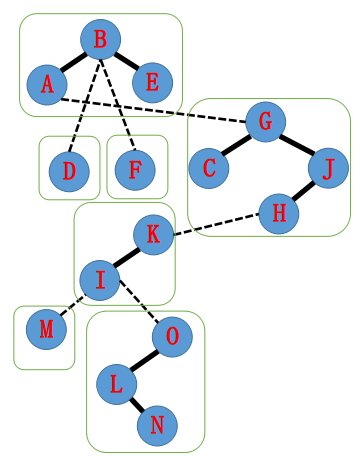
6、access(x)操作:
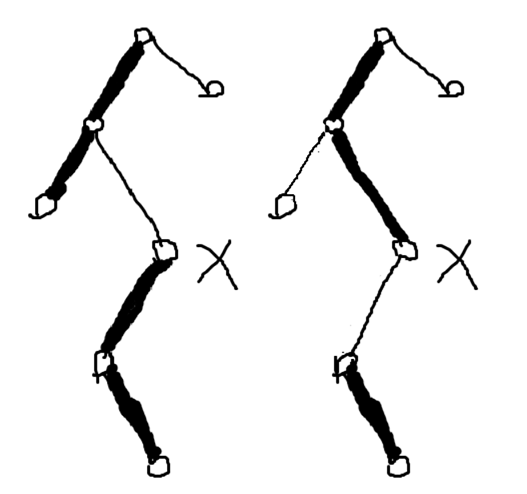
7、splay(x)操作:
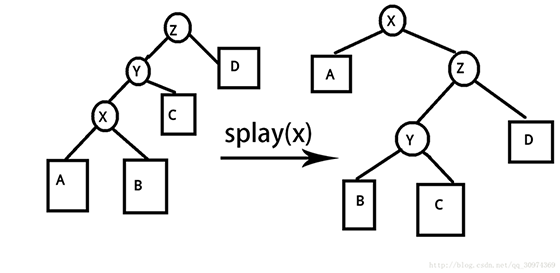
—————————题目—————————
1、Cave 洞穴勘测 HYSBZ - 2049
题意:一开始有n个洞穴,两两之间没有通道。每次将两个洞穴连接或者两个洞穴之间的通道摧毁,或者询问两个洞穴之间能否连通。
思路:LCT模板题。连接则通过link(u,v)实现,摧毁通过cut(u,v)实现,两个洞穴能否连通则考虑u的根和v的根是否相同。

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 const int maxn = 10000 + 10; 5 struct LCT 6 { 7 struct node 8 { 9 int fa, ch[2]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子 10 int reverse;//区间反转标记 11 bool is_root; //是否是所在Splay的根 12 //int siz; 13 //int val; 14 //int sum; 15 }Tree[maxn]; 16 int n; 17 //int v[maxn];//每个结点的值 18 void init() 19 { 20 for (int i = 1; i <= n; i++) 21 { 22 Tree[i].reverse = Tree[i].fa = Tree[i].ch[0] = Tree[i].ch[1] = 0; 23 Tree[i].is_root = true; 24 //Tree[i].siz = 1; 25 //Tree[i].val = Tree[i].sum = v[i]; 26 } 27 } 28 29 bool getson(int x) 30 {//x是否为重儿子 31 return x == Tree[Tree[x].fa].ch[1]; 32 } 33 bool isroot(int x) 34 { 35 return Tree[Tree[x].fa].ch[0] != x && Tree[Tree[x].fa].ch[1] != x; 36 } 37 void pushreverse(int x) 38 { 39 if (!x)return; 40 swap(Tree[x].ch[0], Tree[x].ch[1]); 41 Tree[x].reverse ^= 1; 42 } 43 void pushdown(int x) 44 {//下传反转标记 45 if (Tree[x].reverse) 46 { 47 pushreverse(Tree[x].ch[0]); 48 pushreverse(Tree[x].ch[1]); 49 Tree[x].reverse = 0; 50 } 51 } 52 /* 53 void update(int x) 54 { 55 int l = Tree[x].ch[0], r = Tree[x].ch[1]; 56 Tree[x].siz = Tree[l].siz + Tree[r].siz + 1; 57 Tree[x].sum = Tree[l].sum + Tree[r].sum + Tree[x].val; 58 } 59 */ 60 void rotate(int x) 61 {//将x旋转为根 62 if (Tree[x].is_root)return; 63 int k = getson(x), fa = Tree[x].fa; 64 int fafa = Tree[fa].fa; 65 pushdown(fa); pushdown(x); //先要下传标记 66 Tree[fa].ch[k] = Tree[x].ch[k ^ 1]; 67 if (Tree[x].ch[k ^ 1])Tree[Tree[x].ch[k ^ 1]].fa = fa; 68 Tree[x].ch[k ^ 1] = fa; 69 Tree[fa].fa = x; 70 Tree[x].fa = fafa; 71 if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[1]] = x; 72 else Tree[x].is_root = true, Tree[fa].is_root = false; 73 //update(fa);update(x); //如果维护了信息,就要更新节点 74 } 75 void push(int x) 76 { 77 if (!Tree[x].is_root) push(Tree[x].fa); 78 pushdown(x); 79 } 80 int getFa(int x) 81 {//寻找x在原树的父亲 82 access(x); 83 Splay(x); 84 while (Tree[x].ch[0]) x = Tree[x].ch[0]; 85 return x; 86 } 87 void Splay(int x) 88 {//让x成为Splay的根 89 push(x); //在Splay到根之前,必须先传完反转标记 90 for (int fa; !Tree[x].is_root; rotate(x)) { 91 if (!Tree[fa = Tree[x].fa].is_root) { 92 rotate((getson(x) == getson(fa)) ? fa : x); 93 } 94 } 95 } 96 void access(int x) 97 {//访问某节点。作用是:对于访问的节点x,打通一条从树根(真实的LCT树)到x的重链;如果x往下是重链,那么把x往下的重边改成轻边。 98 int y = 0; 99 do { 100 Splay(x); 101 Tree[Tree[x].ch[1]].is_root = true; 102 Tree[Tree[x].ch[1] = y].is_root = false; 103 //update(x); //如果维护了信息记得更新。 104 x = Tree[y = x].fa; 105 } while (x); 106 } 107 void mroot(int x) 108 {//把某个节点变成树根(这里的根指的是整棵LCT的根) 109 access(x);//使x与根结点处在同一棵splay中 110 Splay(x);//x成为这棵splay的根,x只有左儿子 111 pushreverse(x); 112 } 113 void link(int u, int v) 114 {//连接u所在的LCT和v所在的LCT 115 mroot(u);//先让u成为其所在LCT的根 116 Tree[u].fa = v; 117 } 118 void cut(int u, int v) 119 {//分离出两棵LCT 120 mroot(u); //先让u成为其所在LCT的根 121 access(v); //让u和v在同一棵Splay中 122 Splay(v); //连接u、v,u是v的左儿子 123 pushdown(v); //先下传标记 124 Tree[Tree[v].ch[0]].fa = Tree[v].fa; 125 Tree[Tree[v].ch[0]].is_root = true; 126 Tree[v].fa = 0; 127 Tree[v].ch[0] = 0; 128 //v的左孩子表示v上方相连的重链 129 //update(v); //记得维护信息 130 } 131 bool judge(int u, int v) 132 {//判断u和v是否连通 133 while (Tree[u].fa) u = Tree[u].fa; 134 while (Tree[v].fa) v = Tree[v].fa; 135 return u == v; 136 } 137 }lct; 138 int main() 139 { 140 int m; 141 while (~scanf("%d%d", &lct.n, &m)) 142 { 143 lct.init(); 144 char op[50]; 145 int u, v; 146 for (int i = 1; i <= m; i++) 147 { 148 scanf("%s%d%d", op, &u, &v); 149 if (op[0] == 'Q') 150 { 151 if (lct.judge(u, v)) printf("Yes "); 152 else printf("No "); 153 } 154 else if (op[0] == 'C') 155 { 156 lct.link(u, v); 157 } 158 else 159 { 160 lct.cut(u, v); 161 } 162 } 163 } 164 return 0; 165 }
2、Bounce 弹飞绵羊 HYSBZ - 2002
题意:有n个弹射装置,当绵羊在第i个弹射装置时,会被弹射到第i+val[i]个弹射装置,val数组记录每个弹射装置的弹射系数。有两个操作,要么询问当绵羊站在第x个弹射装置时会经过多少次被弹飞,要么修改某个弹射装置的系数。
思路:可以将第i个弹射装置与第i+val[i]个装置相连,新增第n+1个点作为树根,表示被弹飞。询问次数时即询问当前x到树根的距离即深度,然后-1即可(第n+1个结点不弹射);修改某个弹射装置的系数相当于修改某个结点的父亲,先将原父亲删除,再重新连接父亲。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 const int maxn = 200000 + 10; 6 int val[maxn]; 7 struct LCT 8 { 9 struct node 10 { 11 int fa, ch[2]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子 12 int reverse;//区间反转标记 13 bool is_root; //是否是所在Splay的根 14 int siz; 15 }Tree[maxn]; 16 int n; 17 void init(int maxn) 18 { 19 for (int i = 1; i <= maxn; i++) 20 { 21 Tree[i].reverse = Tree[i].fa = Tree[i].ch[0] = Tree[i].ch[1] = 0; 22 Tree[i].is_root = true; 23 Tree[i].siz = 1; 24 } 25 } 26 27 bool getson(int x) 28 {//x是否为重儿子 29 return x == Tree[Tree[x].fa].ch[1]; 30 } 31 bool isroot(int x) 32 { 33 return Tree[Tree[x].fa].ch[0] != x && Tree[Tree[x].fa].ch[1] != x; 34 } 35 void pushreverse(int x) 36 { 37 if (!x)return; 38 swap(Tree[x].ch[0], Tree[x].ch[1]); 39 Tree[x].reverse ^= 1; 40 } 41 void pushdown(int x) 42 {//下传反转标记 43 if (Tree[x].reverse) 44 { 45 pushreverse(Tree[x].ch[0]); 46 pushreverse(Tree[x].ch[1]); 47 Tree[x].reverse = 0; 48 } 49 } 50 51 void update(int x) 52 { 53 int l = Tree[x].ch[0], r = Tree[x].ch[1]; 54 Tree[x].siz = 1; 55 if (l) Tree[x].siz += Tree[l].siz; 56 if (r) Tree[x].siz += Tree[r].siz; 57 } 58 59 void rotate(int x) 60 {//将x旋转为根 61 if (Tree[x].is_root)return; 62 int k = getson(x), fa = Tree[x].fa; 63 int fafa = Tree[fa].fa; 64 pushdown(fa); pushdown(x); //先要下传标记 65 Tree[fa].ch[k] = Tree[x].ch[k ^ 1]; 66 if (Tree[x].ch[k ^ 1])Tree[Tree[x].ch[k ^ 1]].fa = fa; 67 Tree[x].ch[k ^ 1] = fa; 68 Tree[fa].fa = x; 69 Tree[x].fa = fafa; 70 if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[1]] = x; 71 else Tree[x].is_root = true, Tree[fa].is_root = false; 72 update(fa);update(x); //如果维护了信息,就要更新节点 73 } 74 void push(int x) 75 { 76 if (!Tree[x].is_root) push(Tree[x].fa); 77 pushdown(x); 78 } 79 int getFa(int x) 80 {//寻找x在原树的父亲 81 access(x); 82 Splay(x); 83 while (Tree[x].ch[0]) x = Tree[x].ch[0]; 84 return x; 85 } 86 void Splay(int x) 87 {//让x成为Splay的根 88 push(x); //在Splay到根之前,必须先传完反转标记 89 for (int fa; !Tree[x].is_root; rotate(x)) { 90 if (!Tree[fa = Tree[x].fa].is_root) { 91 rotate((getson(x) == getson(fa)) ? fa : x); 92 } 93 } 94 } 95 void access(int x) 96 {//访问某节点。作用是:对于访问的节点x,打通一条从树根(真实的LCT树)到x的重链;如果x往下是重链,那么把x往下的重边改成轻边。 97 int y = 0; 98 do { 99 Splay(x); 100 Tree[Tree[x].ch[1]].is_root = true; 101 Tree[Tree[x].ch[1] = y].is_root = false; 102 update(x); //如果维护了信息记得更新。 103 x = Tree[y = x].fa; 104 } while (x); 105 } 106 void mroot(int x) 107 {//把某个节点变成树根(这里的根指的是整棵LCT的根) 108 access(x);//使x与根结点处在同一棵splay中 109 Splay(x);//x成为这棵splay的根,x只有左儿子 110 pushreverse(x); 111 } 112 void link(int u, int v) 113 {//连接u所在的LCT和v所在的LCT 114 mroot(u);//先让u成为其所在LCT的根 115 Tree[u].fa = v; 116 Tree[u].is_root = true; 117 } 118 void cut(int u, int v) 119 {//分离出两棵LCT 120 mroot(u); //先让u成为其所在LCT的根 121 access(v); //让u和v在同一棵Splay中 122 Splay(v); //连接u、v,u是v的左儿子 123 pushdown(v); //先下传标记 124 Tree[Tree[v].ch[0]].fa = Tree[v].fa; 125 Tree[Tree[v].ch[0]].is_root = true; 126 Tree[v].fa = 0; 127 Tree[v].ch[0] = 0; 128 //v的左孩子表示v上方相连的重链 129 update(v); //记得维护信息 130 } 131 bool judge(int u, int v) 132 {//判断u和v是否连通 133 while (Tree[u].fa) u = Tree[u].fa; 134 while (Tree[v].fa) v = Tree[v].fa; 135 return u == v; 136 } 137 int Query_deep(int x) 138 {//询问x到LCT根的距离(深度) 139 access(x); 140 Splay(x); 141 return Tree[x].siz; 142 } 143 }lct; 144 int main() 145 { 146 int m; 147 while (~scanf("%d", &lct.n)) 148 { 149 lct.init(lct.n+1);////让n+1表示被弹飞 150 for (int i = 1; i <= lct.n; i++) 151 { 152 scanf("%d", &val[i]); 153 int id = min(i + val[i], lct.n + 1); 154 lct.link(i, id); 155 } 156 lct.mroot(lct.n + 1); 157 scanf("%d", &m); 158 for (int i = 1; i <= m; i++) 159 { 160 int op, x; 161 scanf("%d%d", &op, &x); 162 x++; 163 if (op == 1) printf("%d ", lct.Query_deep(x)-1); 164 else 165 { 166 int v; 167 scanf("%d", &v); 168 int oid = min(x + val[x], lct.n + 1); 169 int nid = min(x + v, lct.n + 1); 170 lct.cut(x, oid); 171 lct.link(x, nid); 172 lct.mroot(lct.n + 1); 173 val[x] = v; 174 } 175 } 176 } 177 return 0; 178 }
3、魔法森林 HYSBZ - 3669
题意:有一个无向图,起点在1,终点在n.每条边有两个权值ai、bi,当且仅当从1到n的路径过程中,身上a的数目不小于路径上的任一条边,b的数目也不小于路径上的任一条边。求最小的a+b。
思路:先将所有边对ai从小到大排序,把所有边拆成两条边插入LCT,自身边权用新的点的点权表示。LCT中结点维护当前splay树中最大的bi以及对应的结点编号。各个结点的连通性用并查集维护。如果对于枚举到的边,其端点之间不连通,则将其拆成1个新的结点和两条边插入LCT;否则,得到该splay中最大的maxb(从splay的根结点得到),以及其对应的边所映射的点的编号(num),如果当前边的bi更小,则需要将原来的边删除,将该边插入(注意,因为把一条边拆成两条边,所以各需要操作两次)。判断结束后,如果当前情形下,起点和终点连通,则更新ans=min(ans,maxb+当前枚举边的ai)。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 const int maxn = 50000 + 10; 7 const int maxm = 100000 + 10; 8 const int INF = 0x7f7f7f7f; 9 struct EDGE 10 { 11 int from, to, a, b; 12 EDGE(int ff=0,int tt=0,int aa=0,int bb=0){} 13 friend bool operator <(const EDGE&e1, const EDGE&e2) 14 { 15 return e1.a < e2.a; 16 } 17 }edge[maxm]; 18 int m,n; 19 //并查集,维护连通性 20 int pre[maxn + maxm]; 21 int Find(int x) 22 { 23 if (pre[x] == x) return x; 24 else 25 { 26 int fa = pre[x]; 27 pre[x] = Find(fa); 28 return pre[x]; 29 } 30 } 31 32 33 struct LCT 34 { 35 struct node 36 { 37 int fa, ch[2]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子 38 int reverse;//区间反转标记 39 bool is_root; //是否是所在Splay的根 40 int siz;//子树结点数目 41 int maxb, num, bi;//splay中最大的bi、与之对应的结点编号、当前结点的bi 42 }Tree[maxn+maxm]; 43 44 void init(int MN) 45 { 46 for (int i = 1; i <= MN; i++) 47 { 48 Tree[i].reverse = Tree[i].fa = Tree[i].ch[0] = Tree[i].ch[1] = 0; 49 Tree[i].is_root = true; 50 Tree[i].num = i; 51 Tree[i].siz = 1; 52 if (i <= n) Tree[i].maxb = Tree[i].bi = 0; 53 else 54 { 55 Tree[i].maxb = Tree[i].bi = edge[i - n].b; 56 } 57 pre[i] = i; 58 } 59 } 60 61 bool getson(int x) 62 {//x是否为重儿子 63 return x == Tree[Tree[x].fa].ch[1]; 64 } 65 bool isroot(int x) 66 { 67 return Tree[Tree[x].fa].ch[0] != x && Tree[Tree[x].fa].ch[1] != x; 68 } 69 void pushreverse(int x) 70 { 71 if (!x)return; 72 swap(Tree[x].ch[0], Tree[x].ch[1]); 73 Tree[x].reverse ^= 1; 74 } 75 void pushdown(int x) 76 {//下传反转标记 77 if (Tree[x].reverse) 78 { 79 pushreverse(Tree[x].ch[0]); 80 pushreverse(Tree[x].ch[1]); 81 Tree[x].reverse = 0; 82 } 83 } 84 85 void update(int x) 86 { 87 int l = Tree[x].ch[0], r = Tree[x].ch[1]; 88 Tree[x].siz = 1; 89 Tree[x].maxb = Tree[x].bi; 90 Tree[x].num = x; 91 if (l) 92 { 93 Tree[x].siz += Tree[l].siz; 94 if (Tree[l].maxb > Tree[x].maxb) Tree[x].maxb = Tree[l].maxb, Tree[x].num = Tree[l].num; 95 } 96 if (r) 97 { 98 Tree[x].siz += Tree[r].siz; 99 if (Tree[r].maxb > Tree[x].maxb) Tree[x].maxb = Tree[r].maxb, Tree[x].num = Tree[r].num; 100 } 101 102 103 } 104 105 void rotate(int x) 106 {//将x旋转为根 107 if (Tree[x].is_root)return; 108 int k = getson(x), fa = Tree[x].fa; 109 int fafa = Tree[fa].fa; 110 pushdown(fa); pushdown(x); //先要下传标记 111 Tree[fa].ch[k] = Tree[x].ch[k ^ 1]; 112 if (Tree[x].ch[k ^ 1])Tree[Tree[x].ch[k ^ 1]].fa = fa; 113 Tree[x].ch[k ^ 1] = fa; 114 Tree[fa].fa = x; 115 Tree[x].fa = fafa; 116 if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[1]] = x; 117 else Tree[x].is_root = true, Tree[fa].is_root = false; 118 update(fa); update(x); //如果维护了信息,就要更新节点 119 } 120 void push(int x) 121 { 122 if (!Tree[x].is_root) push(Tree[x].fa); 123 pushdown(x); 124 } 125 int findroot(int x) 126 {//找到x在原树中的根节点 127 access(x); Splay(x); 128 pushdown(x); 129 while (Tree[x].ch[0]) pushdown(x = Tree[x].ch[0]);//找到深度最小的点即为根节点 130 return x; 131 } 132 void Splay(int x) 133 {//让x成为Splay的根,且x不含右儿子 134 push(x); //在Splay到根之前,必须先传完反转标记 135 for (int fa; !Tree[x].is_root; rotate(x)) { 136 if (!Tree[fa = Tree[x].fa].is_root) { 137 rotate((getson(x) == getson(fa)) ? fa : x); 138 } 139 } 140 } 141 void access(int x) 142 {//访问某节点。作用是:对于访问的节点x,打通一条从树根(真实的LCT树)到x的重链;如果x往下是重链,那么把x往下的重边改成轻边。结束后x没有右儿子(没有深度比他大的点) 143 int y = 0; 144 do { 145 Splay(x); 146 Tree[Tree[x].ch[1]].is_root = true; 147 Tree[Tree[x].ch[1] = y].is_root = false; 148 update(x); //如果维护了信息记得更新。 149 x = Tree[y = x].fa; 150 } while (x); 151 } 152 void mroot(int x) 153 {//把某个节点变成树根(这里的根指的是整棵LCT的根) 154 access(x);//使x与根结点处在同一棵splay中 155 Splay(x);//x成为这棵splay的根,x只有左儿子 156 //由于根节点所在的splay中,根节点没有左儿子(没有深度比他小的节点),将x的左右子树翻转 157 pushreverse(x); 158 } 159 void link(int u, int v) 160 {//连接u所在的LCT和v所在的LCT 161 mroot(u);//先让u成为其所在LCT的根 162 if (findroot(v) != u)Tree[u].fa = v;//如果u与v不在同一棵splay中,就把v设置为u的父亲 163 } 164 void cut(int u, int v) 165 {//分离出两棵LCT 166 mroot(u); //先让u成为其所在LCT的根 167 access(v); //让u和v在同一棵Splay中 168 Splay(v); //连接u、v,u是v的左儿子 169 pushdown(v); //先下传标记 170 if (Tree[v].ch[0]) 171 { 172 Tree[Tree[v].ch[0]].fa = Tree[v].fa; 173 Tree[Tree[v].ch[0]].is_root = true; 174 } 175 Tree[v].fa = 0; Tree[v].ch[0] = 0; 176 //v的左孩子表示v上方相连的重链 177 update(v); //记得维护信息 178 } 179 180 bool judge(int u, int v) 181 {//判断u和v是否连通 182 while (Tree[u].fa) u = Tree[u].fa; 183 while (Tree[v].fa) v = Tree[v].fa; 184 return u == v; 185 } 186 void split(int u, int v) 187 {//获取u->v的路径 188 mroot(u);//让u成为根结点 189 access(v);//访问v 190 Splay(v);//把v转到根结点,此时u的父亲为v 191 } 192 int Query_deep(int x) 193 {//询问x到LCT根的距离(深度) 194 access(x); 195 Splay(x); 196 return Tree[x].siz; 197 } 198 199 }lct; 200 int main() 201 { 202 while (~scanf("%d%d", &n, &m)) 203 { 204 for (int i = 1; i <= m; i++) 205 { 206 scanf("%d%d%d%d", &edge[i].from, &edge[i].to, &edge[i].a, &edge[i].b); 207 } 208 sort(edge + 1, edge + 1 + m); 209 lct.init(n+m); 210 211 int ans = INF; 212 for (int i = 1; i <= m; i++) 213 { 214 if (edge[i].from == edge[i].to)continue; 215 int f_from = Find(edge[i].from),f_to = Find(edge[i].to); 216 if (f_from != f_to) 217 {//不连通 218 lct.link(edge[i].from, i + n);//把一条边拆成2条边和一个点,化作点权 219 lct.link(edge[i].to, i + n); 220 pre[f_to] = pre[f_from] = Find(i + n); 221 } 222 else 223 {//连通 224 lct.split(edge[i].from, edge[i].to); 225 int x = lct.Tree[edge[i].to].num; 226 if (edge[i].b < lct.Tree[x].bi) 227 { 228 lct.cut(edge[i].from, x); 229 lct.cut(edge[i].to, x); 230 lct.link(edge[i].from, i + n); 231 lct.link(edge[i].to, i + n); 232 } 233 } 234 if (Find(1) == Find(n)) 235 { 236 lct.split(1, n); 237 ans = min(ans, lct.Tree[n].maxb + edge[i].a); 238 } 239 } 240 if (ans != INF) printf("%d ", ans); 241 else printf("-1 "); 242 } 243 return 0; 244 }
4、spoj 4155 OTOCI
题意:有n座小岛,一开始两两之间没有桥,每座岛上有若干只企鹅。有三种操作:修改某座岛上的企鹅数目;将某两座岛相连;询问从一座岛到另一座岛路径上所有的企鹅数目。
思路:用LCT维护某座岛的值和子树和。

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 const int maxn = 30000 + 10; 5 int n; 6 struct LCT 7 { 8 struct node 9 { 10 int fa, ch[2]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子 11 int reverse;//区间反转标记 12 bool is_root; //是否是所在Splay的根 13 int val; 14 int sum; 15 }Tree[maxn]; 16 17 void init(int MN) 18 { 19 for (int i = 1; i <= MN; i++) 20 { 21 Tree[i].reverse = Tree[i].fa = Tree[i].ch[0] = Tree[i].ch[1] = 0; 22 Tree[i].is_root = true; 23 } 24 } 25 26 bool getson(int x) 27 {//x是否为重儿子 28 return x == Tree[Tree[x].fa].ch[1]; 29 } 30 bool isroot(int x) 31 { 32 return Tree[Tree[x].fa].ch[0] != x && Tree[Tree[x].fa].ch[1] != x; 33 } 34 void pushreverse(int x) 35 { 36 if (!x)return; 37 swap(Tree[x].ch[0], Tree[x].ch[1]); 38 Tree[x].reverse ^= 1; 39 } 40 void pushdown(int x) 41 {//下传反转标记 42 if (Tree[x].reverse) 43 { 44 pushreverse(Tree[x].ch[0]); 45 pushreverse(Tree[x].ch[1]); 46 Tree[x].reverse = 0; 47 } 48 } 49 50 void update(int x) 51 { 52 int l = Tree[x].ch[0], r = Tree[x].ch[1]; 53 Tree[x].sum = Tree[x].val; 54 if (l) Tree[x].sum += Tree[l].sum; 55 if (r) Tree[x].sum += Tree[r].sum; 56 } 57 58 void rotate(int x) 59 {//将x旋转为根 60 if (Tree[x].is_root)return; 61 int k = getson(x), fa = Tree[x].fa; 62 int fafa = Tree[fa].fa; 63 pushdown(fa); pushdown(x); //先要下传标记 64 Tree[fa].ch[k] = Tree[x].ch[k ^ 1]; 65 if (Tree[x].ch[k ^ 1])Tree[Tree[x].ch[k ^ 1]].fa = fa; 66 Tree[x].ch[k ^ 1] = fa; 67 Tree[fa].fa = x; 68 Tree[x].fa = fafa; 69 if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[1]] = x; 70 else Tree[x].is_root = true, Tree[fa].is_root = false; 71 update(fa); update(x); //如果维护了信息,就要更新节点 72 } 73 void push(int x) 74 { 75 if (!Tree[x].is_root) push(Tree[x].fa); 76 pushdown(x); 77 } 78 int findroot(int x) 79 {//找到x在原树中的根节点 80 access(x); Splay(x); 81 pushdown(x); 82 while (Tree[x].ch[0]) pushdown(x = Tree[x].ch[0]);//找到深度最小的点即为根节点 83 return x; 84 } 85 void Splay(int x) 86 {//让x成为Splay的根,且x不含右儿子 87 push(x); //在Splay到根之前,必须先传完反转标记 88 for (int fa; !Tree[x].is_root; rotate(x)) { 89 if (!Tree[fa = Tree[x].fa].is_root) { 90 rotate((getson(x) == getson(fa)) ? fa : x); 91 } 92 } 93 } 94 void access(int x) 95 {//访问某节点。作用是:对于访问的节点x,打通一条从树根(真实的LCT树)到x的重链;如果x往下是重链,那么把x往下的重边改成轻边。结束后x没有右儿子(没有深度比他大的点) 96 int y = 0; 97 do { 98 Splay(x); 99 Tree[Tree[x].ch[1]].is_root = true; 100 Tree[Tree[x].ch[1] = y].is_root = false; 101 update(x); //如果维护了信息记得更新。 102 x = Tree[y = x].fa; 103 } while (x); 104 } 105 void mroot(int x) 106 {//把某个节点变成树根(这里的根指的是整棵LCT的根) 107 access(x);//使x与根结点处在同一棵splay中 108 Splay(x);//x成为这棵splay的根,x只有左儿子 109 //由于根节点所在的splay中,根节点没有左儿子(没有深度比他小的节点),将x的左右子树翻转 110 pushreverse(x); 111 } 112 void link(int u, int v) 113 {//连接u所在的LCT和v所在的LCT 114 mroot(u);//先让u成为其所在LCT的根 115 if (findroot(v) != u)Tree[u].fa = v;//如果u与v不在同一棵splay中,就把v设置为u的父亲 116 117 } 118 void cut(int u, int v) 119 {//分离出两棵LCT 120 mroot(u); //先让u成为其所在LCT的根 121 access(v); //让u和v在同一棵Splay中 122 Splay(v); //连接u、v,u是v的左儿子 123 pushdown(v); //先下传标记 124 if (Tree[v].ch[0]) 125 { 126 Tree[Tree[v].ch[0]].fa = Tree[v].fa; 127 Tree[Tree[v].ch[0]].is_root = true; 128 } 129 Tree[v].fa = 0; Tree[v].ch[0] = 0; 130 //v的左孩子表示v上方相连的重链 131 update(v); //记得维护信息 132 } 133 134 bool judge(int u, int v) 135 {//判断u和v是否连通 136 while (Tree[u].fa) u = Tree[u].fa; 137 while (Tree[v].fa) v = Tree[v].fa; 138 return u == v; 139 } 140 void split(int u, int v) 141 {//获取u->v的路径 142 mroot(u);//让u成为根结点 143 access(v);//访问v 144 Splay(v);//把v转到根结点,此时u的父亲为v,u是v的左儿子 145 } 146 147 void modify(int x, int v) 148 {//改变点值 149 access(x); 150 Splay(x); 151 Tree[x].val = v; 152 update(x); 153 } 154 155 }lct; 156 int main() 157 { 158 scanf("%d", &n); 159 lct.init(n); 160 for (int i = 1; i <= n; i++) 161 { 162 scanf("%d", &lct.Tree[i].val); 163 lct.Tree[i].sum = lct.Tree[i].val; 164 } 165 int m; 166 scanf("%d", &m); 167 char op[20]; 168 while (m--) 169 { 170 scanf("%s", op); 171 if (op[0] == 'e') 172 { 173 int u, v; 174 scanf("%d%d", &u, &v); 175 if (lct.judge(u, v)) 176 { 177 lct.split(u, v); 178 printf("%d ", lct.Tree[v].sum ); 179 } 180 else 181 { 182 printf("impossible "); 183 } 184 } 185 else if (op[0] == 'b') 186 { 187 int u, v; 188 scanf("%d%d", &u, &v); 189 if (!lct.judge(u, v)) 190 { 191 printf("yes "); 192 lct.link(u, v); 193 } 194 else printf("no "); 195 } 196 else 197 { 198 int u, w; 199 scanf("%d%d", &u, &w); 200 lct.modify(u, w); 201 } 202 } 203 return 0; 204 }
5、Caves and Tunnels URAL - 1553
题意:有n个洞穴,由n-1条通道相连。有两种操作:将某个洞穴的辐射水平升高一定值;询问两个洞穴之间最大的辐射值。
思路:LCT维护当前结点的辐射值以及子树的最大辐射值。亦可以使用树链剖分来解决,因为没有链的变动,其实是个静态树。

1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 using namespace std; 5 const int maxn = 100000 + 10; 6 int n, q; 7 struct LCT 8 { 9 struct node 10 { 11 int fa, ch[2]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子 12 int reverse;//区间反转标记 13 bool is_root; //是否是所在Splay的根 14 int val; 15 int maxv; 16 }Tree[maxn]; 17 18 void init(int MN) 19 { 20 for (int i = 1; i <= MN; i++) 21 { 22 Tree[i].reverse = Tree[i].fa = Tree[i].ch[0] = Tree[i].ch[1] = 0; 23 Tree[i].is_root = true; 24 Tree[i].val = Tree[i].maxv = 0; 25 } 26 } 27 28 bool getson(int x) 29 {//x是否为重儿子 30 return x == Tree[Tree[x].fa].ch[1]; 31 } 32 bool isroot(int x) 33 { 34 return Tree[Tree[x].fa].ch[0] != x && Tree[Tree[x].fa].ch[1] != x; 35 } 36 void pushreverse(int x) 37 { 38 if (!x)return; 39 swap(Tree[x].ch[0], Tree[x].ch[1]); 40 Tree[x].reverse ^= 1; 41 } 42 void pushdown(int x) 43 {//下传反转标记 44 if (Tree[x].reverse) 45 { 46 pushreverse(Tree[x].ch[0]); 47 pushreverse(Tree[x].ch[1]); 48 Tree[x].reverse = 0; 49 } 50 } 51 52 void update(int x) 53 { 54 int l = Tree[x].ch[0], r = Tree[x].ch[1]; 55 Tree[x].maxv = Tree[x].val; 56 if (l) Tree[x].maxv = max(Tree[x].maxv, Tree[l].maxv); 57 if (r) Tree[x].maxv = max(Tree[x].maxv, Tree[r].maxv); 58 } 59 60 void rotate(int x) 61 {//将x旋转为根 62 if (Tree[x].is_root)return; 63 int k = getson(x), fa = Tree[x].fa; 64 int fafa = Tree[fa].fa; 65 pushdown(fa); pushdown(x); //先要下传标记 66 Tree[fa].ch[k] = Tree[x].ch[k ^ 1]; 67 if (Tree[x].ch[k ^ 1])Tree[Tree[x].ch[k ^ 1]].fa = fa; 68 Tree[x].ch[k ^ 1] = fa; 69 Tree[fa].fa = x; 70 Tree[x].fa = fafa; 71 if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[1]] = x; 72 else Tree[x].is_root = true, Tree[fa].is_root = false; 73 update(fa); update(x); //如果维护了信息,就要更新节点 74 } 75 void push(int x) 76 { 77 if (!Tree[x].is_root) push(Tree[x].fa); 78 pushdown(x); 79 } 80 int findroot(int x) 81 {//找到x在原树中的根节点 82 access(x); Splay(x); 83 pushdown(x); 84 while (Tree[x].ch[0]) pushdown(x = Tree[x].ch[0]);//找到深度最小的点即为根节点 85 return x; 86 } 87 void Splay(int x) 88 {//让x成为Splay的根,且x不含右儿子 89 push(x); //在Splay到根之前,必须先传完反转标记 90 for (int fa; !Tree[x].is_root; rotate(x)) { 91 if (!Tree[fa = Tree[x].fa].is_root) { 92 rotate((getson(x) == getson(fa)) ? fa : x); 93 } 94 } 95 } 96 void access(int x) 97 {//访问某节点。作用是:对于访问的节点x,打通一条从树根(真实的LCT树)到x的重链;如果x往下是重链,那么把x往下的重边改成轻边。结束后x没有右儿子(没有深度比他大的点) 98 int y = 0; 99 do { 100 Splay(x); 101 Tree[Tree[x].ch[1]].is_root = true; 102 Tree[Tree[x].ch[1] = y].is_root = false; 103 update(x); //如果维护了信息记得更新。 104 x = Tree[y = x].fa; 105 } while (x); 106 } 107 void mroot(int x) 108 {//把某个节点变成树根(这里的根指的是整棵LCT的根) 109 access(x);//使x与根结点处在同一棵splay中 110 Splay(x);//x成为这棵splay的根,x只有左儿子 111 //由于根节点所在的splay中,根节点没有左儿子(没有深度比他小的节点),将x的左右子树翻转 112 pushreverse(x); 113 } 114 void link(int u, int v) 115 {//连接u所在的LCT和v所在的LCT 116 mroot(u);//先让u成为其所在LCT的根 117 if (findroot(v) != u)Tree[u].fa = v;//如果u与v不在同一棵splay中,就把v设置为u的父亲 118 } 119 void cut(int u, int v) 120 {//分离出两棵LCT 121 mroot(u); //先让u成为其所在LCT的根 122 access(v); //让u和v在同一棵Splay中 123 Splay(v); //连接u、v,u是v的左儿子 124 pushdown(v); //先下传标记 125 if (Tree[v].ch[0]) 126 { 127 Tree[Tree[v].ch[0]].fa = Tree[v].fa; 128 Tree[Tree[v].ch[0]].is_root = true; 129 } 130 Tree[v].fa = 0; Tree[v].ch[0] = 0; 131 //v的左孩子表示v上方相连的重链 132 update(v); //记得维护信息 133 } 134 135 bool judge(int u, int v) 136 {//判断u和v是否连通 137 while (Tree[u].fa) u = Tree[u].fa; 138 while (Tree[v].fa) v = Tree[v].fa; 139 return u == v; 140 } 141 void split(int u, int v) 142 {//获取u->v的路径 143 mroot(u);//让u成为根结点 144 access(v);//访问v 145 Splay(v);//把v转到根结点,此时u的父亲为v 146 } 147 148 void modify(int x, int v) 149 {//改变点值 150 access(x); 151 Splay(x); 152 Tree[x].val += v; 153 update(x); 154 155 } 156 157 }lct; 158 char op[20]; 159 int main() 160 { 161 scanf("%d", &n); 162 lct.init(n); 163 for (int i = 1; i <= n - 1; i++) 164 { 165 int u, v; 166 scanf("%d%d", &u, &v); 167 lct.link(u, v); 168 } 169 scanf("%d", &q); 170 while (q--) 171 { 172 scanf("%s", op); 173 if (op[0] == 'I') 174 { 175 int u, w; 176 scanf("%d%d", &u, &w); 177 lct.modify(u, w); 178 } 179 else 180 { 181 int u, v; 182 scanf("%d%d", &u, &v); 183 lct.split(u, v); 184 printf("%d ", lct.Tree[v].maxv); 185 } 186 } 187 return 0; 188 }
