棋盘覆盖——分治 C

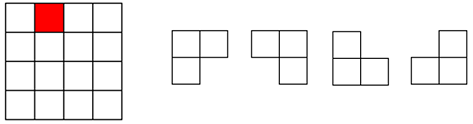
在一个2^k × 2^k 个方格组成的棋盘中，有一特殊方格。

在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的棋盘上除特殊方格以外的所有方格，L型骨牌不能旋转，且任何两个L型骨牌不得重叠覆盖。

Sample Input

2
2 1 2
1 1 1

Sample Output

c*bb
ccdb
cddd
ccdd

*d
dd

解题思路：

当 k>0 时，将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘，如下图所示：

#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
int e[300][300];
int tap = 0;

inline void print(int size) {
    for(int i = 1; i <= size; i++) {
        for(int j = 1; j <= size; j++) {
            //printf("%d ", e[i][j]);
            if(e[i][j] == e[i+1][j] && e[i][j] == e[i][j+1] && i+1 <= size && j+1 <= size) {
                printf("a");
            } else if(e[i][j] == e[i][j-1] && e[i][j] == e[i+1][j-1] && j-1 >= 1 && i+1 <= size) {
                printf("a");
            } else if(e[i][j] == e[i-1][j] && e[i][j] == e[i-1][j+1] && i-1 >= 1 && j+1 <= size) {
                printf("a");
            } else if(e[i][j] == e[i][j+1] && e[i][j] == e[i+1][j+1] && j+1 <= size && i+1 <= size) {
                printf("b");
            } else if(e[i][j] == e[i][j-1] && e[i][j] == e[i+1][j] && j-1 >= 1 && i+1 <= size) {
                printf("b");
            } else if(e[i][j] == e[i-1][j-1] && e[i][j] == e[i-1][j] && i-1 >= 1 && j-1 >= 1) {
                printf("b");
            } else if(e[i][j] == e[i+1][j] && e[i][j] == e[i+1][j+1] && i+1 <= size && j+1 <=size) {
                printf("c");
            } else if(e[i][j] == e[i-1][j] && e[i][j] == e[i][j+1] && i-1 >= 1 && j+1 <= size) {
                printf("c");
            } else if(e[i][j] == e[i-1][j-1] && e[i][j] == e[i][j-1] && i-1 >= 1 && j-1 >=1) {
                printf("c");
            } else if(e[i][j] == e[i-1][j+1] && e[i][j] == e[i][j+1] && i-1 >= 1 && j+1 <=size) {
                printf("d");
            } else if(e[i][j] == e[i][j-1] && e[i][j] == e[i-1][j] && j-1 >= 1 && i-1 >= 1) {
                printf("d");
            } else if(e[i][j] == e[i+1][j-1] && e[i][j] == e[i+1][j] && i+1 <= size && j-1 >= 1) {
                printf("d");
            } else if(e[i][j] == -1) printf("*");
            //printf(" ");
        }
        printf("
");
    }
}
/*
 * 把一个棋盘分为四等份，如果特殊点在左上角，则在棋盘剩下三角的靠近顶点处变为特殊点，此为一个L型特殊点。
 * 把棋盘分化，分条件判断四个等分的棋盘，递归处理。
*/

inline void chess(int lx, int ly, int x, int y, int size) {
    /*
     * lx：棋盘左上角的行坐标
     * ly：棋盘左上角的列坐标
     * x：特殊点行坐标
     * y：特殊点列坐标
     * size：棋盘大小
    */
    if(size == 1) return ;

    int k = size / 2; //分化后的棋盘大小

    int t = tap++;

    if(y < ly + k && x < lx + k) { /* 特殊点在左上角 */
        chess(lx, ly, x, y, k); /* 递归处理左上角方块 */
    } else {
        /* 不在左上角，则需要在左上角的右下角处构建一个特殊点 */
        e[lx + k - 1][ly + k - 1] = t;
        chess(lx, ly, lx + k - 1, ly + k - 1, k);
    }

    if(y >= ly + k && x < lx + k) { /* 特殊点在右上角 */
        chess(lx, ly + k, x, y, k);
    } else {
        e[lx + k - 1][ly + k] = t;
        chess(lx, ly + k, lx + k - 1, ly + k, k);
    }

    if(y< ly + k && x >= lx + k) { /* 特殊点在左下角 */
        chess(lx + k, ly, x, y, k);
    } else {
        e[lx + k][ly + k - 1] = t;
        chess(lx + k, ly, lx + k, ly + k - 1, k);
    }

    if(y >= ly + k && x >= lx + k) { /* 特殊点在右下角 */
        chess(lx + k, ly + k, x, y, k);
    } else {
        e[lx + k][ly + k] = t;
        chess(lx + k, ly + k, lx + k, ly + k, k);
    }

}
int main( ) {
    int t;
    scanf("%d", &t);
    int k, x, y;

    while(t--) {
        tap = 0;
        for(int i = 1; i <= 300; i++) {
            for(int j = 1; j <= 300; j++) {
                e[i][j] = 0;
            }
        }

        scanf("%d %d %d", &k, &x, &y);
        int size = 1;
        for(int i = 0; i < k; i++) size *= 2;
        e[x][y] = -1;

        chess(1, 1, x, y, size);
        print(size);

    }

    return 0;
}