// 2019年西电暑期集训
// [7月9日]基础数论:https://cn.vjudge.net/contest/309097
A - Visible Lattice Points
题目大意:
平面上有N*N个格点,问从原点(0,0)能够看到多少个不被遮挡的点。
数据范围:1<=N<=1000,测试组数:1<=C<=1000。
分析及代码:
暴力计算复杂度N*N*C,肯定T。看题目所给几组样例,也没有发现有什么规律。
注意到点的分布的对称性,对于每一列(x=xi),记录在直线y=x以下能看到的点的坐标:
(1,1)
(2,1)
(3,1),(3,2)
(4,1),(4,3)
(5,1),(5,2),(5,3),(5,4)
......
可以发现直线x=xi上的点的个数为与xi互质的个数,即欧拉函数值phi(xi)。
由对称性,(1,1)重复计算,加上点(1,0)与(0,1),所以本题答案为2*∑phi(xi) + 1。

#include <iostream> #include <cstdio> using namespace std; const int maxn = 1010; int phi[maxn+1]; void phi_table(int n) { // O(nlogn) n以内欧拉表 int i, j; for(i=1;i<=n;i++) phi[i] = i; for(i=2;i<=n;i+=2) phi[i] /= 2; for(i=3;i<=n;i+=2) { if(phi[i]==i) { for(j=i;j<=n;j+=i) phi[j] = phi[j] / i * (i - 1); } } for(int i=1;i<=n;i++) { // 前缀和 phi[i] += phi[i-1]; } } int main() { phi_table(1010); int T, t = 0, n; cin>>T; while(t++<T) { scanf("%d", &n); printf("%d %d %d ", t, n, phi[n]*2+1); } return 0; }
B - Super A^B mod C
题目大意:
计算A^B (mod C)的结果,其中1<=A,C<=1000000000,1<=B<=10^1000000。
分析及代码:
B的数位长度达到了1000000位,即使利用快速幂logn的算法也有些勉强。。。
依稀记得有一个欧拉定理(费马小定理),计算当m为素数时a^b % m结果为a^(b%(m-1)),指数立刻收缩到了ll范围内。
这里需要用到a和m不互质情况下的欧拉降幂公式:
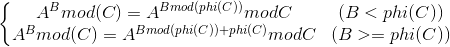
至于为什么我AC的代码指数没有加上phi(C)也过了,我也不懂O.O

#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> using namespace std; const int maxn = 1000100; typedef long long ll; ll a, c; char b[maxn]; ll phi(ll x) { // 欧拉函数 ll res = x; for(int i=2;i<=x/i;i++) { if(x%i==0) { res = res/i*(i-1); while(x%i==0) x/=i; } } if(x>1) res = res/x*(x-1); return res; } ll pow(ll a, ll n) { // 快速幂 ll res = 1; while(n) { if(n&1) res = res * a % c; a = a*a % c; n >>= 1; } return res; } int main() { while(scanf("%lld", &a)!=EOF) { scanf("%s", b); scanf("%d", &c); ll exp = 0, p = phi(c); for(int i=0;b[i];i++) { exp *= 10; exp += b[i]-'0'; exp %= p; } // exp += p; printf("%lld ", pow(a, exp)); } return 0; }
D - The Euler function
题目大意:
求一段区间的欧拉函数值的和。(2<a<b<3000000)
分析及代码:
欧拉函数裸题,使用O(nlogn)欧拉筛预处理。
(预先求前缀和的算法比直接区间求和要慢。。。)

#include <iostream> #include <cstdio> using namespace std; const int maxn = 3000010; typedef long long ll; ll phi[maxn]; void phi_table(int n) { int i, j; for(i=1;i<=n;i++) phi[i] = i; for(i=2;i<=n;i+=2) phi[i] /= 2; for(i=3;i<=n;i+=2) { if(phi[i]==i) { for(j=i;j<=n;j+=i) phi[j] = phi[j] / i * (i - 1); } } for(int i=1;i<=n;i++) { phi[i] += phi[i-1]; } } int main() { phi_table(3000000); int a, b; while(scanf("%d %d", &a, &b)!=EOF) { // 此题直接写for循环更快 printf("%lld ", phi[b]-phi[a-1]); } return 0; }
E - Strange Way to Express Integers
题目大意:
中国剩余定理裸题。。。
分析及代码:
还不是特别熟悉,网上找了份mi不互质的模板,稍微改改就直接A了。

#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> using namespace std; typedef long long ll; const int maxn = 1010; ll exgcd(ll a, ll b, ll& x, ll& y) { ll d = a; if(b!=0) { d = exgcd(b, a%b, y, x); y -= (a/b) * x; } else { x = 1; y = 0; } return d; } ll a[maxn], m[maxn], n; ll CRT() { if (n == 1) { if (m[0] > a[0]) return a[0]; else return -1; } ll x, y, d; for (int i = 1; i < n; i++) { if (m[i] <= a[i]) return -1; d = exgcd(m[0], m[i], x, y); if ((a[i] - a[0]) % d != 0) return -1; //不能整除则无解 ll t = m[i] / d; x = ((a[i] - a[0]) / d * x % t + t) % t; //第0个与第i个模线性方程的特解 a[0] = x * m[0] + a[0]; m[0] = m[0] * m[i] / d; a[0] = (a[0] % m[0] + m[0]) % m[0]; } return a[0]; } int main() { while(scanf("%lld", &n)!=EOF) { for(int i=0;i<n;i++) { scanf("%lld %lld", &m[i], &a[i]); } printf("%lld ", CRT()); } return 0; }
F - C Looooops
题目大意:
求A + Cx = B (mod 2^k) 的x最小正整数解。
分析及代码:
上式变形得到
C*x + 2^k*y = B-A
利用扩展欧几里得ax+by=gcd(a,b)解该同余方程,得到x。
- 若 (B-A) % gcd(a, b) 不为0,则无解。
- 否则 x = x * (B-A) / gcd(a, b) ,得到 原方程的特解。
- 原方程的全部解为 x + m * C / gcd(a, b), m∈Z
- 令 s = C / gcd(a, b)
- 所以最小的整数解为 (x%s + s) % s

#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> using namespace std; typedef long long ll; // d = gcd(a, b) = ax + by ll exgcd(ll a, ll b, ll& x, ll& y) { ll d = a; if(b!=0) { d = exgcd(b, a%b, y, x); y -= (a/b) * x; } else { x = 1; y = 0; } return d; } // Ax = B (mod C) ll solve(ll A, ll B, ll C){ ll x, y; ll d = exgcd(A, C, x, y); if(B%d!=0){ return -1; // 无解 } x *= B/d; ll s = C/d; return (x%s + s)%s; } int main() { int A, B, C, k; while(scanf("%d %d %d %d", &A, &B, &C, &k)!=EOF && A+B+C+k) { ll ans = solve(C, B-A, (ll)1<<k); // A+Cx = B (mod 2^k) if(ans==-1) { printf("FOREVER "); } else { printf("%lld ", ans); } } return 0; }
G - Divisors
题目大意:
求组合数C(n, k)的因子个数。(0 ≤ k ≤ n ≤ 431)
分析及代码:
一看n,k都不大,直接将定义式的连乘项分解,统计每个素因子的出现次数。
然后有那啥公式,每个素因子个数+1后再相乘即为答案,交一发T了。
加上素数筛,还是T了。优化 了下,T了。改对n,k的记忆化,还是T了。
。。。
来学习一下求n!某个因子个数的方法:(去年博客)
// 公式:cnt = [n/p] + [n/p^2] + [n/p^3] +...+ [n/p^k] // 核心代码: int cnt = 0; while(n) { cnt += n/p; n /= p; }
终于AC的代码:

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> using namespace std; const int maxn = 440; int cnt[maxn], n, k; int p[maxn], num; void init() { for(int i=2;i<maxn;i++) { bool isp = true; for(int j=2;j*j<=i;j++) { if(i%j==0) { isp = false; break; } } if(isp) p[num++] = i; } } int cal(int n, int p) { int res = 0; while(n) { res += n/p; n /= p; } return res; } int main() { init(); while(scanf("%d %d", &n, &k)!=EOF) { long long ans = 1; for(int i=0;i<num && p[i]<=n;i++) { // 没有p[i]<=n TLE!!! long long cnt = 0; cnt += cal(n, p[i]); cnt -= cal(k, p[i]); cnt -= cal(n-k, p[i]); ans *= (cnt+1); } printf("%lld ", ans); } return 0; }
H - 青蛙的约会
题目大意:
同F题,求同余方程 x-y + (m-n) * k = 0 (mod L) k的最小正整数解。
分析及代码:
按照F的推导过程慢慢推吧。

#include<cstdio> #include<iostream> #include<algorithm> using namespace std; typedef long long ll; // d = gcd(a, b) = ax + by ll exgcd(ll a, ll b, ll& x, ll& y) { ll d = a; if(b!=0) { d = exgcd(b, a%b, y, x); y -= (a/b) * x; } else { x = 1; y = 0; } return d; } // Ax = B (mod C) ll solve(ll A, ll B, ll C){ ll x, y; ll d = exgcd(A, C, x, y); if(B%d!=0){ return -1; // 无解 } x *= B/d; ll s = C/d; return (x%s + s)%s; } int main() { ll x, y, m, n, L; cin>>x>>y>>m>>n>>L; ll ans; if(m>n) ans = solve(m-n, y-x, L); // m-n>0 else ans = solve(n-m, x-y, L); if(ans==-1) { printf("Impossible "); } else { printf("%lld ", ans); } return 0; }
I - Semi-prime H-numbers
题目大意:
定义类似4*k+1的正整数为H数。H数分为两种,H素数和H合数,合数中只能分解成两个H素数相乘形式的为H半素数。
求一个区间内H半素数的个数。
分析及代码:
模仿素数筛的写法,很容易实现O(nlogn)的H素数筛法。
在筛选过程中,将H数为标记为三种类别,素数、半素数、合数。
最后将所有含有半素数标记的取出,采用upper_bound二分查找可以快速得到答案。

#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> using namespace std; const int maxn = 1000100; int Htype[maxn]; // 0:prime 2:semi-prime 1:composite //int p[maxn], num; int pp[maxn], num2; void init() { // Htype[1] = isp[5] = 0; for(int i=5;i<maxn;i+=4) { if(!Htype[i]) { //p[num++] = i; if(i<maxn/i) Htype[i*i] = 2; for(int j=2*i;j<maxn;j+=i) { if(j%4==1) { Htype[j] = 1; if((j/i)%4==1 && !Htype[j/i]) Htype[j] = 2; } } } } for(int i=5;i<maxn;i+=4) { if(Htype[i]==2) { pp[num2++] = i; } } } int main() { init(); int h; while(scanf("%d", &h)!=EOF && h) { printf("%d ", h); printf("%d ", upper_bound(pp, pp+num2, h) - pp); } return 0; }
(未完待续)
