// 2019.10.7 练习赛
// 赛题来源:2018 ICPC 焦作区域赛
// CF链接:http://codeforces.com/gym/102028
A Xu Xiake in Henan Province
题目大意
有四个旅游地,给出 n 个人去四个地方的旅游次数,根据他去过旅游地个数输出相应等级。
思路
签到题。。。(队友在干嘛呀,10min过去了600人交题了啊我们怎么还没AC
AC代码
#include<iostream>
#include<cstdio>
using namespace std;
const char* ans[5] = {
"Typically Otaku","Eye-opener", "Young Traveller",
"Excellent Traveller", "Contemporary Xu Xiake"};
int main() {
int T; cin>>T;
while(T--) {
int cnt = 0;
for(int i=0;i<4;i++) {
int A; scanf("%d", &A);
if(A>0) ++cnt;
}
printf("%s
", ans[cnt]);
}
return 0;
}
D Keiichi Tsuchiya the Drift King
题目大意
如图,求最小的赛车车道宽度 w ,使赛车能够保证车头与内道相切的情况下漂移过弯。
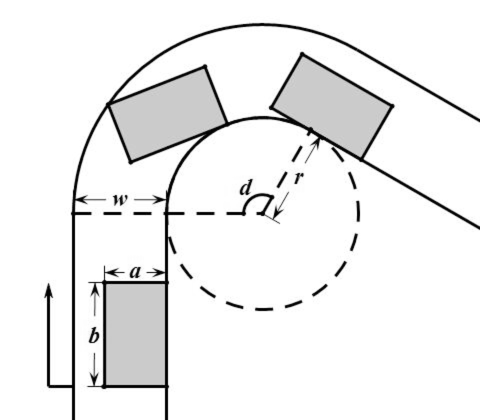
思路
很容易推导出,车尾与外车道接触时得到最小宽度 (w = sqrt{(b^2+(a+r)^2} - r) 。
为什么弯道角度没有用上呢?原来出弯道时车尾可能还没与外后侧圆弧赛道接触,这时 w 能取得更小值。
AC代码
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const double pi = acos(-1);
int main() {
int T; cin>>T;
double a, b, r, d;
while(T--) {
scanf("%lf %lf %lf %lf", &a, &b, &r, &d);
d = d/180*pi;
double w = sqrt(b*b+(a+r)*(a+r));
double ang = acos((a+r)/w);
if(d>ang)
printf("%.10lf
", w-r);
else
printf("%.10lf
", w*cos(ang-d)-r);
}
return 0;
}
EE Resistors in Parallel
题目大意
对于第 n 号电阻,电阻值为 n 的全部非平方因子电阻值的并联,(若含有平方因子,则为无穷大,相当于没有贡献)。给定 n<=10^100,求其中最小的电阻。
思路
简单分析可以发现组成的电阻值一定是一组互质的小电阻及其乘积,如 {1,2}, {1, 3}, {1, 2, 3, 6}, {1, 2, 3, 5, 6, 15, 30} ...
打表发现结果为 (p_1p_2...p_k over (p_1+1)(p_2+1)...(p_k+1)) , 其中 (p_i) 为素数。
由于 n 非常大,Python大法好。
AC代码
def gcd(a, b):
if b==0:
return a
return gcd(b, a%b)
vis = [False]*1000
primes = []
for i in range(2, 1000):
if not vis[i] :
primes.append(i)
for j in range(2*i, 1000, i):
vis[j] = True
T = int(input().rstrip())
for i in range(T):
n = int(input())
fz = 1
fm = 1
k = 0
while fz*primes[k]<=n:
fz *= primes[k]
fm *= primes[k]+1
k = k+1
g = gcd(fz, fm)
print("{}/{}".format(fz//g, fm//g))
# print("%d/%d"% (fz//g, fm//g))
F Honeycomb
题目大意
给定一个蜂巢图形,求从起点 S 到终点 T 的最短路的路径长度。
BFS跑一下就完了。
// 比赛时候被PDF坑了,以为空格要自己补上。。浪费时间。。
AC代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<map>
#define mp make_pair
using namespace std;
typedef pair<int, int> pii;
typedef pair<pii, int> piii;
int len[4*1024];
char mat[4*1024][6*1024];
int n, m;
int sx, sy, ex, ey;
map<pii, bool> vis;
queue<piii> q;
const int dx[] = {-1, 1, -1, 1, 2, -2};
const int dy[] = {-3, -3, 3, 3, 0, 0};
int bfs() {
vis.clear();
while(q.size()) q.pop();
q.push(mp(mp(sx, sy), 1));
vis[mp(sx, sy)] = 1;
while(q.size()) {
piii now = q.front(); q.pop();
int x = now.first.first, y = now.first.second;
if(x==ex && y==ey) {
return now.second;
}
for(int i=0;i<6;i++) {
int nx = x+dx[i], ny = y+dy[i];
// if(nx>=1 && ny>=1 && nx<=4*n+3 && ny<=len[nx] && mat[nx][ny]==' ') {
if(mat[nx][ny]==' ') {
pii next = mp(nx+dx[i], ny+dy[i]);
if(vis.find(next)==vis.end()) {
q.push(mp(next, now.second+1));
vis[next] = 1;
}
}
}
}
return -1;
}
int main() {
int T; cin>>T;
while(T--) {
scanf("%d %d", &n, &m);
getchar();
for(int i=1;i<=4*n+3;i++) {
gets(mat[i]+1);
len[i] = strlen(mat[i]+1);
for(int j=1;j<=len[i];j++) {
if(mat[i][j]=='S') {
sx = i, sy = j;
} else if(mat[i][j]=='T') {
ex = i, ey = j;
}
}
}
printf("%d
", bfs());
}
return 0;
}
I Distance
题目大意
数轴上有 n 个点, 求分别取 k = 1~n个点,使取得的点两两之间距离和最大,输出最大值。
思路
贪心法。交替取两端的点,能使每步都能取到最大值。
(只需要维护前缀和与后缀和,我sb了在那写树状数组没调出来扔给队友,队友WA了自闭了又还给我)
AC代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
const int maxn = 100100;
int n;
ll arr[maxn];
int main() {
int T; cin>>T;
while(T--) {
scanf("%d", &n);
arr[1] = 0;
for(int i=2;i<=n;i++) {
scanf("%d", &arr[i]);
arr[i] += arr[i-1];
}
arr[1+n] = 0;
int l = 0, r = 0;
ll ans = 0, left = 0, right = 0;
for(int i=1;i<=n;i++) {
if(i%2==1) {
// cout<<arr[l+1]<<endl;
ans += l*arr[l+1] - left + right - r*arr[l+1];
left += arr[l+1];
l++;
}
else {
// cout<<arr[n-r]<<endl;
ans += l*arr[n-r] - left + right - r*arr[n-r];
right += arr[n-r];
r++;
}
printf("%lld%c", ans, i==n?'
':' ');
}
}
return 0;
}