HDU 1978 How many ways

How many ways

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 1654    Accepted Submission(s): 1016

Problem Description

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下： 1.机器人一开始在棋盘的起始点并有起始点所标有的能量。 2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。 3.机器人不能在原地停留。 4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。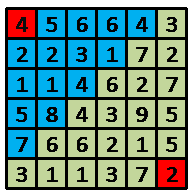如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)
点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。 我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

 

Input

第一行输入一个整数T,表示数据的组数。 对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

Output

对于每一组数据输出方式总数对10000取模的结果.

 

Sample Input

1

6 6

4 5 6 6 4 3

2 2 3 1 7 2

1 1 4 6 2 7

5 8 4 3 9 5

7 6 6 2 1 5

3 1 1 3 7 2

 

Sample Output

3948

 

Author

xhd

 

Source

2008杭电集训队选拔赛

 

Recommend

wangye

 

 

 

 

记忆化搜索+DP..

题目中“他将只有终点所标记的能量”是解题的关键啊！一开始还老想剩余能量怎么处理.....悲剧。

这题可以分为两种DP方式，一种是当前的这个点可以到达其他点的方法数和能到达当前点的方法数。。

两种状态转移方程也差不多。

下面分别是两种方法的AC代码

 

1,

#include<stdio.h>
#include<string.h>

const int maxn=120;

int n,m;
int map[maxn][maxn];
int dp[maxn][maxn];

int min(int a,int b){
    return a<b?a:b;
}

int DFS(int x,int y,int k){
    if(x==n && y==m)
        return 1;
    if(dp[x][y]!=0)
        return dp[x][y];
    for(int i=0;i<=min(k,n-x);i++)
        for(int j=0;j<=min(k-i,m-y);j++){
            if(i==0 && j==0)
                continue;
            dp[x][y]+=DFS(x+i,y+j,map[x+i][y+j]);
            dp[x][y]%=10000;
        }
    return dp[x][y];
}

int main(){

    //freopen("input.txt","r",stdin);

    int t;
    scanf("%d",&t);
    while(t--){
        memset(map,0,sizeof(map));
        memset(dp,0,sizeof(dp));
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                scanf("%d",&map[i][j]);
        DFS(1,1,map[1][1]);
        printf("%d\n",dp[1][1]);
    }
    return 0;
}

2,

#include<stdio.h>
#include<string.h>

int dp[120][120];

int main(){

    //freopen("input.txt","r",stdin);

    int t,n,m;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        memset(dp,0,sizeof(dp));
        dp[0][0]=1;
        int num;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++){
                scanf("%d",&num);
                for(int x=0;x<=num;x++)
                    for(int y=0;y<=num-x;y++){
                        if(x==0 && y==0)
                            continue;
                        dp[i+x][j+y]=(dp[i+x][j+y]+dp[i][j])%10000;
                    }
            }
        printf("%d\n",dp[n-1][m-1]);
    }
    return 0;
}