一道C++面试题的误区

一道C++面试题的误区

问题：寻找数组中的最小值和最大值。

 

一道很简单的题目，一般有下面4种解法：

1 遍历两次，每次分别找出最小值和最大值。

2 只遍历一次，每次取出的元素先与已找到的最小值比较，再与已找到的最大值比较。

3 每次取两个元素，将较小者与已找到的最小值比较，将较大者与已找到的最大值比较。

4 分治：将数组划分成两半，分别找出两边的最小值、最大值，则最小值、最大值分别是两边最小值的较小者、两边最大值的较大者。

 

这4种算法，哪种效率最高，哪种最低？

后两种算法只要进行1.5*N次比较，因而网上有不少解答都将它们列为最佳答案。但是，算法4用到了递归，而递归法函数调用的开销是很大的，这就注定了该算法的效率肯定不高。那么，算法3就是最高效的吗？还是用代码来验证吧。

 

后面的代码，对每种算法都实现了两个函数（假设数组长度为N）：

算法1：solve_1a与solve_1b，后者加入两个临时变量，编译器可以将变量储存在寄存器中，不用每次循环都要写内存。比较次数为2*N次。

算法2：solve_2a与solve_2b，前者每次循环必比较2次，后者最好情况下(递减数组)只要比较1次，但最差情况下（递增数组）则要比较2次，比较次数为：N到2 * N次。

算法3：solve_3a与solve_3b，前者每次循环取头尾两元素（从两头往中间取），后者取相邻两元素。比较次数为1.5 * N次。

算法4：solve_4a与solve_4b，后者返回一个结构（只有两个元素），编译器优化可以通过两个寄存器返回该结构，减少写内存次数。（检查gcc产生的汇编，确认有进行该优化）。比较次数为1.5 * N次。

 

下面是测试结果：（数组长度为6e7，每种测4次取平均值）

	所用时间（毫秒，GCC 4.5）					所用时间（毫秒，VC 2010）
函数名	递增	递减	乱序1	乱序2	乱序3	递增	递减	乱序1	乱序2	乱序3
1a 两次遍历	175	183	187	179	179	199	203	176	187	175
1b 两次遍历（优化）	175	179	171	171	172	183	234	175	187	172
2a 一次遍历	105	105	105	129	105	105	132	105	109	105
2b 一次遍历（优化）	105	90	105	109	105	109	109	105	113	105
3a 取头尾两元素	85	85	246	246	246	86	82	261	261	261
3b 取相邻两元素	93	101	238	242	238	93	101	258	257	253
4a 分治法	316	359	867	863	867	773	777	1554	1558	1558
4b 分治法（优化）	273	289	824	824	828	648	656	1347	1340	1339

编译参数：tdm-gcc 4.5.2-dw2: g++ -O3 -s -Wextra –Wall     VC 2010: cl /Ox /EHsc /nologo /W3

很明显，“分治”法的效率远低于其它3种算法。对前3种算法，将数组长度增加到1e8，并对十组随机数组进行测试，得到结果：

 

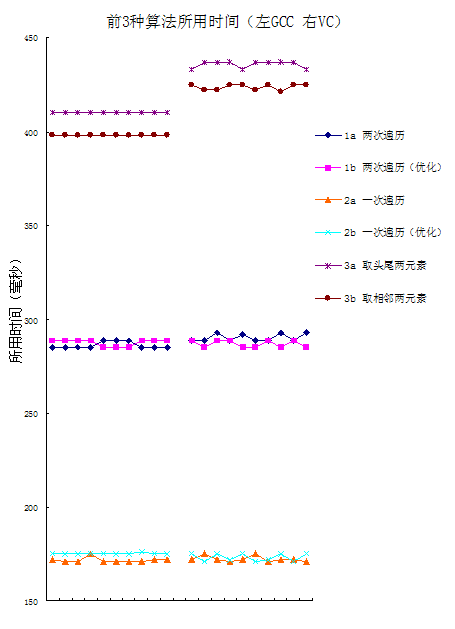
从上面的表和图可以看出，算法3在数组有序时，运行效率很高（但与算法2相差不大），而在乱序时，甚至比两次遍历都慢。乱序时：算法2效率最高，算法1次之，算法3效率最低。

算法2a和算法2b的效率差不多，有时算法2a的效率还略高。算法2a，每次循环都要比较2次，算法2b每次循环要比较1到2次，但由于前者的两次比较是无关的，后者的比较是相关的（第一次比较的结果决定是否进行第二次比较），在现代CPU“指令预测”等技术前，算法2a在某些情况下能比较算法2b更高效。

算法3的效率也不是绝对最差的，上面的随机数组是通过随机产生一些数得到，如果把它改为对数组的元素进行 “随机洗牌”，就得到下面的结果（所得的新数据与上面的数据和并，下图中第一、三列是上面的数据，第二、四列是改用“随机洗牌”后得到的新数据）：

 

 

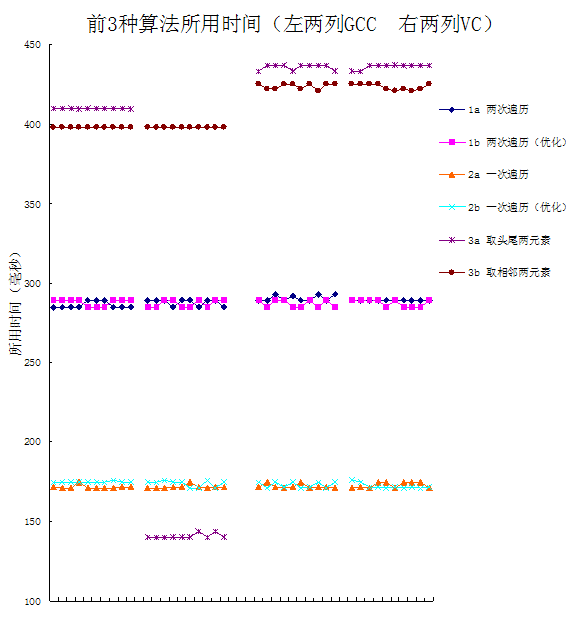
从图可以看出，改用“随机洗牌”法得到乱序数组后，VC的结果没发生改变，GCC除了函数3a，结果也没改变，但是“3a一次取头尾两元素”却成为最高效的算法，但其效率和 “一次遍历取一个元素” 法，相差并不是太大。因而可以说，在单线程环境下，“一次遍历取一个元素”这个最容易想到的方法，反而是本题的最佳解法。

   

算法上的最优，并不一定是实际上的最优，快排和堆排序就是一个典型的例子，虽然快排最坏情况下的复杂度是O(N^2)，而堆排序始终是O(N lgN)，但实际运用中，一个好的快排实现一般都比堆排序快很多。何况这4种算法的复杂度还都是O(N)。为了在最坏情况下节省0.5 * N次比较，进行的所谓优化，得到的结果很可能与所期望的恰恰相反。

 

 插入代码总是失败，还是给附件吧。 找出数组的最小值和最大值 测试代码

 

作者： flyinghearts 
出处： http://www.cnblogs.com/flyinghearts/ 
本文采用知识共享署名-非商业性使用-相同方式共享 2.5 中国大陆许可协议进行许可，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。