更新至4.20
原文为SIGGRAH2013上Epic Games工程师Brian Karis的分享,虽然现在已经是8102年了,但总体变动不大,依然有学习的价值。

图1.UE4渗透者Demo
介绍-Introduction
大约在一年前(2012年),我们决定投入一些时间去提升我们的着色模型并且包含一个更加基于物理的材质工作流。它部分驱动自渲染更真实的图像的需求,但是我们也对我们通过更基于物理的方法进行材质创建、使用分层材质可能达到的目标感兴趣。艺术家感觉这可能是对工作流和质量的一个巨大的提升,并且我已经在另一个工作室第一时间看到了这些成效,在那里我们已经过渡到离线混合的材质层。我们的其中一位技术美术在Epic在着色器中做分层的实验,实现了结果很有希望,这成为了一个额外的需求。
为了支持这个方向,我们知道材质的分层需要简单,并且高效。迪士尼的演讲来的时间十分完美,涉及到了他们的基于物理的着色和使用Wreck-It Ralph的材质模型。Brent Burley 展示了一个非常小的材质参数集合可以足够精致的表现离线特性的电影渲染。他童谣展示了一个相当实用的着色模型可以紧密的适用于大多数采样的材质。他们的工作成为了我们的一个灵感和基础,并且像他们的“规则”相似,我们也决定去定义一个我们自己的系统的目标。
实时性能-Real-Time Performance
·首要的是,它需要在每次许多可见灯光的条件下高效地使用。
简化复杂度-Reduced Complexity
·参数尽可能的少。大批的参数不仅会造成决定无力,反复试验和错误,或者相互关联的属性对于一个预期效果需要许多的值来改变。
·我们需要能够使用基于图像的光照和解析光源可切换,所以参数必须在多有的光照类型中表现一致。
直观的界面-Intuitive Interface
·我们更倾向易于理解的值,而不是像折射率这样的物理参数。
感知线性-Perceptually Linear
·我们希望通过蒙版支持分层,但是我们只能承受逐像素一次着色的负担。这意味着混合参数着色必须尽可能的匹配着色结果的混合。
简单掌握-Easy to Master
·我们想要避免需要电介质和导体的技术理解,同时最小化创建基本的貌似物理的材质所需要的努力。
健壮-Robust
·错误的创建物理上不可信的材质很困难。
·参数的所有合并应该尽可能的健壮和可信。
善于表现-Expressive
·延迟渲染限制了我们可以使用的着色模型的数量,所以我们的基本着色模型需要足够描述覆盖显示世界中99%的材质。
·所有可分层的材质需要共享相同的参数集在他们中混合。
灵活-Flexible
·其他的项目和授权可能不共享相同的真实感目标,所以也需要足够灵活来允许非真实感渲染。
着色模型-Shading Model
漫反射双向反射分布函数-Diffuse BRDF
我们评估了Burley的漫反射模型但是只观察到与Lambertain模型相比轻微的差别(等式1),所以我们不能证明额外的消耗的合理性。除此之外,任何更复杂的漫反射模型很难高效的使用基于图像或球面谐调的光照。因此,我们不在评估其他选择上投入精力。

这里Cdiff是材质的漫反射率。
微表面镜面反射双向反射分布函数-Microfacet Specular BRDF
常规的Cook-Torrance微表面镜面反射着色模型是:
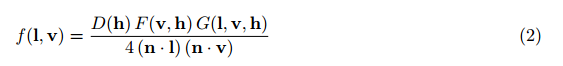
我们开始使用迪士尼的模型,并且评估了比起更高效的替代,每一项的重要性。这远比听起来困难;每个项的公布的公式不一定使用相同的输入参数,但这对于正确的比较是至关重要的。
镜面反射D-Specular D
对于法线分布函数(NDF),我们发现迪士尼选择的GGX/Trowbridge-Reitz的成本是值得的。对比使用Blinn-Phong的额外消耗相当的小,并且提供了更长的“拖尾”的明显且自然的表现吸引了我们的艺术家。我们也采用了迪士尼的二次参数化α=Roughness^2。
![]()
镜面反射G-Specular G
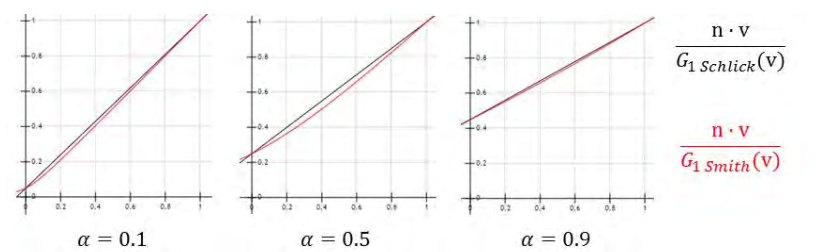
比起其他项,我们对于镜面反射集合衰减项评估了更多的选择。最后,我们选择了Schlick模型,但是令k=α/2,为了更好地适应GGX的Smith模型。应用这个修改,在α=1时Schlick模型恰好匹配Smith,并且在[0,1]范围内相当的接近近似值(图2)。我们也选择去使用迪士尼的修改来降低“热度”通过在平方前使用(Roughness+1)/2重映射粗糙度。注意到这个调整仅用于解析的光源时很重要的;如果在基于图像的光照中应用,结果会导致在掠射角变得很暗。

镜面反射F-Specular F
对于菲涅尔,我们做出使用Schlick近似的经典选择,但是有一点修改,我们使用了球面高斯Spherical Gaussian近似来代替power。这稍微提高了计算效率,并且差异微不可察,公式为:
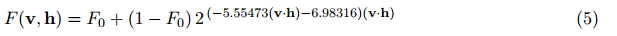
图2.使用k=α/2的Schlick非常接近Smith匹配
基于图像的光照-Image-Based Lighting
为了在基于图像的光照使用这个着色模型,需要解决辐射率积分,这通常使用重要性采样来完成。下面的等式描述了这个数值积分:
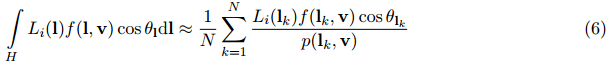
下面的HLSL代码展示了如何在我们的着色模型中实现(以下与原文略不一致,使用了4.20的代码替换):

1 float4 ImportanceSampleGGX( float2 E, float Roughness ) 2 { 3 float m = Roughness * Roughness; 4 float m2 = m * m; 5 6 float Phi = 2 * PI * E.x; 7 float CosTheta = sqrt( (1 - E.y) / ( 1 + (m2 - 1) * E.y ) ); 8 float SinTheta = sqrt( 1 - CosTheta * CosTheta ); 9 10 float3 H; 11 H.x = SinTheta * cos( Phi ); 12 H.y = SinTheta * sin( Phi ); 13 H.z = CosTheta; 14 15 float d = ( CosTheta * m2 - CosTheta ) * CosTheta + 1; 16 float D = m2 / ( PI*d*d ); 17 float PDF = D * CosTheta; 18 19 return float4( H, PDF ); 20 }

1 float3 SpecularIBL( uint2 Random, float3 SpecularColor, float Roughness, float3 N, float3 V ) 2 { 3 float3 SpecularLighting = 0; 4 5 const uint NumSamples = 32; 6 for( uint i = 0; i < NumSamples; i++ ) 7 { 8 float2 E = Hammersley( i, NumSamples, Random ); 9 float3 H = TangentToWorld( ImportanceSampleGGX( E, Roughness ).xyz, N ); 10 float3 L = 2 * dot( V, H ) * H - V; 11 12 float NoV = saturate( dot( N, V ) ); 13 float NoL = saturate( dot( N, L ) ); 14 float NoH = saturate( dot( N, H ) ); 15 float VoH = saturate( dot( V, H ) ); 16 17 if( NoL > 0 ) 18 { 19 float3 SampleColor = AmbientCubemap.SampleLevel( AmbientCubemapSampler, L, 0 ).rgb; 20 21 float Vis = Vis_SmithJointApprox( Roughness, NoV, NoL ); 22 float Fc = pow( 1 - VoH, 5 ); 23 float3 F = (1 - Fc) * SpecularColor + Fc; 24 25 // Incident light = SampleColor * NoL 26 // Microfacet specular = D*G*F / (4*NoL*NoV) = D*Vis*F 27 // pdf = D * NoH / (4 * VoH) 28 SpecularLighting += SampleColor * F * ( NoL * Vis * (4 * VoH / NoH) ); 29 } 30 } 31 32 return SpecularLighting / NumSamples; 33 }
即使有重要性采样,许多的样本仍然需要被采集。样本数量可以通过mip maps显著的减少,但是数量仍然需要大于16以满足足够的数量(原文1024次采样,4.20为32次采样)。因为我们对于局部反射逐像素的在许多环境贴图中混合,我们可以只能实际为每一个提供一个样本。
分离和近似-Split Sum Approximation
为了实现这个,我们通过分离它成为两项之和来近似以上的和。每一个分离的和可以之后被预计算。对于一个常数Li(l)这个近似是准确的,并且对于常规的环境相当的精确。
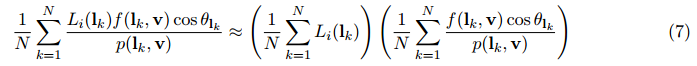
预积分环境贴图-Pre-Filtered Environment Map
我们对于不同的粗糙度值,预计算第一个和项并且将结果保存在CubeMap的mip-map层级中。这是在游戏工业使用的典型方式。一个较小的区别是,我们使用了重要性采样和我们的着色模型中的GGX分布对环境贴图做了卷积。因为这是微表面模型,分布的形状改变依赖于到表面上的观察角度,所以我们假设这个角度是0,例如,n=v=r。各向同性的假设是近似的第二个来源,并且它不幸地意味着我们不会在掠射角获得漫长的反射。比起分离的和近似,实际上这是我们IBL解决方案中更大的错误来源。正如下面代码展示的,我们已经发现使用cosθlk可以实现更佳的结果。

1 float3 PrefilterEnvMap( uint2 Random, float Roughness, float3 R ) 2 { 3 float3 FilteredColor = 0; 4 float Weight = 0; 5 6 const uint NumSamples = 64; 7 for( uint i = 0; i < NumSamples; i++ ) 8 { 9 float2 E = Hammersley( i, NumSamples, Random ); 10 float3 H = TangentToWorld( ImportanceSampleGGX( E, Roughness ).xyz, R ); 11 float3 L = 2 * dot( R, H ) * H - R; 12 13 float NoL = saturate( dot( R, L ) ); 14 if( NoL > 0 ) 15 { 16 FilteredColor += AmbientCubemap.SampleLevel( AmbientCubemapSampler, L, 0 ).rgb * NoL; 17 Weight += NoL; 18 } 19 } 20 21 return FilteredColor / max( Weight, 0.001 ); 22 }
环境双向反射分布函数-Environment BRDF
第二个和项包含了剩下的其他所有。这与用一个纯白色的环境对镜面反射双向反射分布函数进行积分操作是一样的,例如,Li(lk)=1。通过Schlick的菲涅尔代替:F(v,h)=F0+(1-F0)(1-v·h)^5,我们发现F0可以因式分解到积分外。
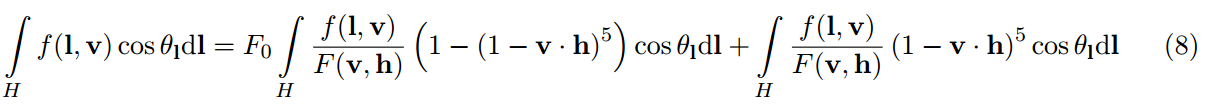
这余下了两个输入(粗糙度Roughness和cosθv),和两个输出(F0的缩放和偏移),所有的值都在[0,1]的范围内。我们预计算这个函数的结果,并且保存到一个2D的查找表中。

在完成这项工作之后,我们发现目前的和同时进行的研究,几乎都是和我们一致的结果。Whilst Gotanda使用了3D查找表,Drobot优化它到2D的查找表,就和我们所做的那样。另外,作为这个课题的一员——Lazarov又向前迈进了一步,展示了相似积分的一对解析近似。

1 float3 IntegrateBRDF( uint2 Random, float Roughness, float NoV ) 2 { 3 float3 V; 4 V.x = sqrt( 1.0f - NoV * NoV ); // sin 5 V.y = 0; 6 V.z = NoV; // cos 7 8 float A = 0; 9 float B = 0; 10 float C = 0; 11 12 const uint NumSamples = 64; 13 for( uint i = 0; i < NumSamples; i++ ) 14 { 15 float2 E = Hammersley( i, NumSamples, Random ); 16 17 { 18 float3 H = ImportanceSampleGGX( E, Roughness ).xyz; 19 float3 L = 2 * dot( V, H ) * H - V; 20 21 float NoL = saturate( L.z ); 22 float NoH = saturate( H.z ); 23 float VoH = saturate( dot( V, H ) ); 24 25 if( NoL > 0 ) 26 { 27 float Vis = Vis_SmithJointApprox( Roughness, NoV, NoL ); 28 29 float a = Square( Roughness ); 30 float a2 = a*a; 31 float Vis_SmithV = NoL * sqrt( NoV * (NoV - NoV * a2) + a2 ); 32 float Vis_SmithL = NoV * sqrt( NoL * (NoL - NoL * a2) + a2 ); 33 //float Vis = 0.5 * rcp( Vis_SmithV + Vis_SmithL ); 34 35 // Incident light = NoL 36 // pdf = D * NoH / (4 * VoH) 37 // NoL * Vis / pdf 38 float NoL_Vis_PDF = NoL * Vis * (4 * VoH / NoH); 39 40 float Fc = pow( 1 - VoH, 5 ); 41 A += (1 - Fc) * NoL_Vis_PDF; 42 B += Fc * NoL_Vis_PDF; 43 } 44 } 45 46 { 47 float3 L = CosineSampleHemisphere( E ).xyz; 48 float3 H = normalize(V + L); 49 50 float NoL = saturate( L.z ); 51 float NoH = saturate( H.z ); 52 float VoH = saturate( dot( V, H ) ); 53 54 float FD90 = ( 0.5 + 2 * VoH * VoH ) * Roughness; 55 float FdV = 1 + (FD90 - 1) * pow( 1 - NoV, 5 ); 56 float FdL = 1 + (FD90 - 1) * pow( 1 - NoL, 5 ); 57 C += FdV * FdL * ( 1 - 0.3333 * Roughness ); 58 } 59 } 60 61 return float3( A, B, C ) / NumSamples; 62 }
最后,为了近似重要性采样的引用,我们将这两个预计算的和相乘。

1 float3 ApproximateSpecularIBL( uint2 Random, float3 SpecularColor, float Roughness, float3 N, float3 V ) 2 { 3 // Function replaced with prefiltered environment map sample 4 float3 R = 2 * dot( V, N ) * N - V; 5 float3 PrefilteredColor = PrefilterEnvMap( Random, Roughness, R ); 6 //float3 PrefilteredColor = FilterEnvMap( Random, Roughness, N, V ); 7 8 // Function replaced with 2D texture sample 9 float NoV = saturate( dot( N, V ) ); 10 float2 AB = IntegrateBRDF( Random, Roughness, NoV ).xy; 11 12 return PrefilteredColor * ( SpecularColor * AB.x + AB.y ); 13 }

图4:最上方为参考,分离和近似位于中间,包含n=v假设的完全近似在最底部。放射对称性假设引入了最大的错误,但是合并近似依然和参考十分近似。

图5:与图4相同的对比但是为电介质。
材质模型-Material Mode
我们的材质模式是迪士尼的材质模型的简化版本,着眼于实时渲染的效率。限制参数的数量对于优化G-Buffer的空间十分重要,减少贴图的空间占用和存取,并且最小化在像素着色器中混合材质图形的成本。
下面是我们的基础材质模型:
基本颜色BaseColor 单一颜色。更容易理解的概念
金属度Metallic 不需要理解电介质和导体的反射率,更少的错误空间
粗糙度Roughness 它的概念非常清晰,相反的是光泽度gloss通常需要解释
凹槽Cavity 用于小规模的遮蔽(实际版本:镜面反射Specular 用于在非金属表面上控制镜面反射量)
Note-Cavity比AO更高频,通常和AO混合使用,AO是更低频的信息,所以这里Cavity并不是被AO替换,而是Specular。
基本颜色,金属度,粗糙度都和迪士尼的模型相同,但是沟槽参数没有介绍,所以它值得解释。凹槽是用于指定来自小于我们运行时阴影系统可以处理的几何体遮蔽,通常由于几何体是在法线贴图表现的。例如,地板木板间的裂缝和衣服的接缝。
最值得注意的疏忽是镜面反射参数。我们实际上直到我们的《渗透者》Demo时完成一直在使用它,但最后我们并不喜欢它。首先,我们觉得“镜面反射”是一个糟糕的参数名称,造成了很多的误解并且对于艺术家从控制镜面反射强度到粗糙度的过渡有负面影响。艺术家和图形程序一般都忘记他的范围或者当它的真正默认值是Burley的0.5(对应4%反射率)时,假设默认值为1。在实际使用镜面反射的情况,几乎完全是为了小规模的阴影。我们发现可变的折射率(IOR)对于非金属来说是相对不重要的,所以我们最近用更容易理解的凹槽参数替换了镜面反射。非金属的F0现在是常数0.04。(实际版本:引擎中依然使用镜面反射参数,镜面反射参数输入范围[0,1],默认为0.5,F0的值为镜面反射参数*0.08。)
经历-Experiences
有一种情况,到现在我已经见过很多次了。我告诉艺术家要开始过渡到使用不同的粗糙度:“使用粗糙度 ,就像你过去使用的镜面反射颜色一样”,不久之后我激动惊喜的听到:“这行得通!但是一个有趣的评论随之而来:“粗糙度感觉颠倒了。”事实证明,艺术家们想要看到他们制作的纹理,正如更亮的纹素相当于更亮的镜面反射高光。如果图像存储了粗糙度,那么亮度相当于更高的粗糙度,这将产生低强度的高光。
我收到无数次的一个问题:“金属度是二进制吗?”最初我的解释是混合或分层材质的微妙之处。但之后我就明白了,最好只说“是的!”原因是,一开始艺术家不愿意将参数设置为绝对的;我通常发现金属的金属度为0.8。材质分层—接下来进行讨论—应该是描述在99%的情况下金属度不会是0或1。
在过渡期间,我们遇到了一些问题,这些材质是无法再复制的。其中最重要的一些问题来自《堡垒之夜》,这是一款目前在Epic制作的游戏。《堡垒之夜》有一个非真实感的艺术方向并且对于漫反射和镜面反射有目的地使用互补色,在我们的新材质模型中是不物理上真实的,而且是故意特意这样做的。经过长时间的讨论,我们决定继续支持旧的DiffuseColor/SpecularColor作为引擎的开关,以保持《堡垒之夜》的质量,因为它已经开发了很长的时间。然而,我们并不认为新模型排除了非真实感渲染,正如迪斯尼在《无敌破坏王》的使用示范的那样,我们打算在未来的项目使用它。
材质分层-Material Layering
在我们之前的方法中,共享库的混合材质图层提供了许多的好处,这是为了单独指定材质参数,参数值来自于为每个特殊的模型制作的纹理:
•利用大量资产重新进行工作。
•减少单一资产的复杂度。
•统一并集中了定义游戏表现的材质,简易化艺术和技术的方向。
为了完全接受这个新的工作流程,我们需要重新思考我们的工具。从UE3早期开始,虚幻引擎拥有一个特色的基于节点的材质编辑器。这个节点图指定了输入(纹理、常量),操作和输出,它们被编译成着色器代码。
尽管材质分层是这项工作的主要目标,但令人惊讶的是,只需要很小的添加工具层面的需求去支持材质图层的创作和混合。UE4的材质编辑器的节点图部分,早已可以被组合为函数,用于多种材质。这种功能是实现材质图层自然的选择。把材质图层放在我们的基于节点的编辑器之中,而不是作为一个之上的固定的函数系统,允许以可编程的方式映射和组合图层。
为了简化工作流程,我们添加了一个新的数据类型,即材质属性,它包含了所有的材质输出数据。这种新类型,像我们的其他类型一样,可以作为单独引脚在材质函数中传入或传出,通过连线传递,并直接输出。有了这些变化,材质图层可以和纹理一样拖进来作为输入,组合,操作和输出。事实上,大多数材质图往往更简单,因为图层的采纳作为自定义一个特殊材质的主要事情是图层的映射和混合的。这比过去存在的特定参数操作要简单得多。
由于有一小部分感性的材质参数,这实际上对图层用着色器完全混合是可行的。我们认为,在纯粹的离线的组合系统它提供了一个实质的质量提高。由于能够以不同的频率映射数据,纹理数据的可见分辨率可以极高:逐顶点或低频纹理数据可以是唯一的,混合层遮罩,法线贴图和沟槽贴图是逐网格指定的,并且材质图层是在网格的表面平铺的。更高级的情况下可能会使用更多的频率。由于着色器成本,尽管我们事实上限制了我们可以使用的图层数量,但我们的艺术家还没有发现限制对他们造成问题。
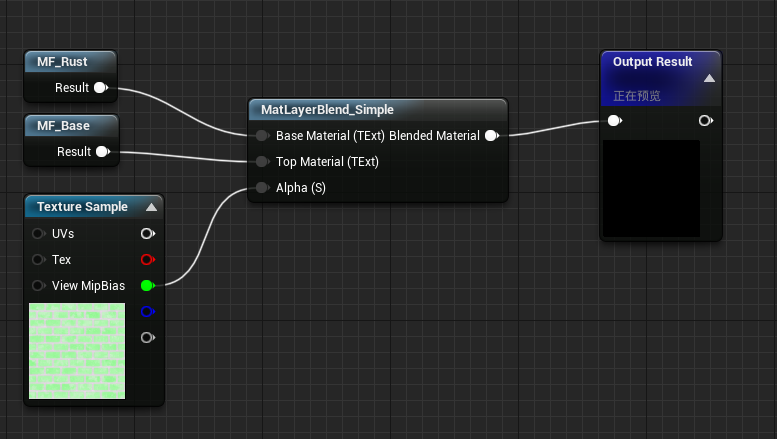
图6.UE4材质编辑器的简单材质分层
一个值得关注的方面,案例中,艺术家们通过将一个网格分割成多个部分来解决着色器内的分层限制,导致更多的绘制调用。尽管由于CPU方面的代码优化,我们希望在UE4中获得更佳的绘制调用数量,这似乎在未来是一个问题来源。一个我们还没有研究的领域就是使用动态分支在一个层有百分之百覆盖的区域来减少着色器成本。
到目前为止,我们对材质图层的经验是非常积极正面的。我们已经看到了生产效率和质量的大幅提高。我们希望通过简化查找和预览图层的方式来改进艺术家的材质图层库界面。除了我们当前的实时系统之外,我们还打算研究一个离线合成/烘焙系统,以支持更多的层并提供更好的可扩展性。

图7.用锈迹交换和混合的许多材质图层

图8.利用多频率细节的材质分层结果
光照模型-Lighting Mode
正如着色一样,我们希望通过使它更基于物理来提高我们的光照模型。我们投入研究的两个领域是光照衰减和非精确发射源——通常被称之为面积光源。
提高光照衰减是相当简单直接的:我们采纳了物理精确的反平方衰减并切换到光度学的光通量的亮度单位。这就是说,我们需要解决的一个并发问题是,这种衰减函数没有值为0时的距离(无穷远处)。但是为了效率——无论是实时还是离线计算——我们依然需要人工限制灯光的影响。有许多的方式可以实现,但是我们选择以多数的灯光影响保持相对不受影响的方式去修改反平方函数,同时依然提供了一个柔和到0的过渡。一个比较好的性质是通过修改灯光的半径不会改变它的有效亮度,这当光照被艺术性的锁定时很重要,但是因为性能的原因灯光范围依然需要调整。
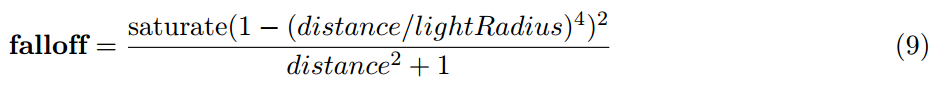
这里分母中的1是为了防止距离接近光源是函数值爆发。它可以暴露一个艺术家可控制的参数,例如物理矫正不理想的时候。
特别在场景中有许多局部光源的时候,这个简单的改变产生的质量差异意味着这很可能是巴克外卖(?)的最大的冲击。

图9:反平方衰减实现更自然的结果
面积光照-Area Lights
面积光源不只是生成更真实的图像。当使用基于物理材质的时候他们也相当重要。我们发现没有这些,艺术家直觉地倾向于避免绘制非常低粗糙度,因为这会导致极小的镜面反射高光,这看起来并不自然。必要的是,他们尽力去再现制作来自精确光源的面积光照效果。
不幸的是,它的反作用导致了一个着色和光照之间的耦合,打破了基于物理的渲染的核心原则:当用在与他们创建时并不一致的光照环境时,材质不能被修改。
面积光是一个研究的活跃领域。在离线渲染中,常规的解决方案是使用统一采样或者重要性采样从光源表面上的许多点处进行照明。对于实时渲染这是完全不实用的。在讨论解决方案的可行性之前,这些是我们的需求:
·一致的材质表现
-漫反射BRDF和镜面反射BRDF评估的能量并没有明显的不同。
·当立体角接近0时,接近点光源模型
-我们不想丢失我们的着色模型的任何一方面来实现它。
·足够快可以在任何地方使用
-否则,我们无法解决上述提及的”偏颇粗糙度“问题。
公告板反射-Billboard Reflections
公告板反射是IBL可以用于离散的光源一种形式。一张存储了发射光的2D图像,被映射到一个3D空间的矩形。和环境贴图预过滤相似的是,图像对不同大小的镜面反射分布椎体预过滤。计算镜面反射着色从这个图像中可以被认为作为椎体追踪的一种形式,这里一个椎体近似为镜面反射NDF。椎体中心射线与公告板的平面相交。图像空间的相交点之后被用于纹理坐标,并且椎体的半径在相交处被用于推导一个近似预过滤的mip级别。悲痛的是,图像能以一个直接了当的方式表现十分复杂的面积光源,公告板反射因为多种原因无法满足我们第二个需求:
·图像是在平面预过滤的,所以在图像空间表现出一个受限制的立体角。
·当射线未于平面相交的时候,没有数据。
·光照向量,l,是未知的或者假定是反射向量。
椎体相交-Cone Intersection
椎体追踪不需要预过滤;可以解析地实现。我们试验过使用Oat的椎体-椎体相交等式追踪球体上的椎体的一个版本,但是实际操作起来成本过于昂贵。最近,Drobot用一个面向着色点的圆盘与椎体相交提供了一个替代方案。NDF的多项式近似之后在相交区域分段积分。
随着Drobot最近的进展,这似乎是一个有趣的研究领域。但以目前的形式,它没有满足我们的要求。由于是哦那个了一个椎体,镜面反射分布必须是径向对称地。这就排除了拉伸的高光,微表面镜面反射模型的一个非常重要的特性。除此之外,像公告板反射,着色模型不需要一个定义的光照向量。
镜面反射D修改-Specular D Modification
去年,我们展示了基于光源的立体角修改镜面反射分布的方法。它的理论是考虑一个光源的分布与一个对应椎体角D(h)相同。通过增加两个圆锥体的角度来推导出一个新的圆锥可以将一个分布与另一个分布的卷积近似。为了实现这个,根据等式3转换α到一个有效的椎体角,加上光源的角度,再转换回去。α'用于代替α。我们使用下面的近似来实现:

尽管高效,这个技术不幸的是不满足我们的第一个要求,因为当用大的面积光照亮非常光滑的材质时表现的粗糙。这听上去显而易见,但是在镜面反射NDF简洁(例如Blinn-Phong)的时候这个技术做的更好,从而更好的匹配光源分布。对于我们选择的着色模型(基于GGX),并不可行。

图10:左边为参考,右边是镜面反射D修改方法。因为在掠射角处失去了球形近似效果很差,并且光滑材质,例如擦亮的黄铜头盔,看起来粗糙。
代表点-Representative Point
如果对于一个特定的着色点,我们可以将所有来自面积光的光看作来自光源表面的一个单一代表点,我们的着色模型可以直接使用。一个合理的选择最大贡献的点。对于一个Phong分布,就是光源上与反射射线角度最小的点。
这个技术之前已经被发表,但是能量守恒并没有解决。通过移动发射光源的原点,我们高效的提高了光源的立体角但是并没有对额外的能量进行补偿。对它的校正比起除以立体角稍微有些复杂,因为能量差异取决于镜面反射的分布。例如,改变入射光的方向对于一个粗糙材质会导致很小的能量变化,但是对于一个光滑的材质能量的改变很大。
球形光-Sphere Lights
如果球在地平线之上,球形光的辐照度等于点光。尽管反直觉,这意味着当球落在地平线之下的时候如果我们接受误差,我们仅仅需要处理镜面反射光照。我们通过寻找距离射线最小的点近似发现与反射射线之间最小的角度的点。对于一个球这是简单明了的:
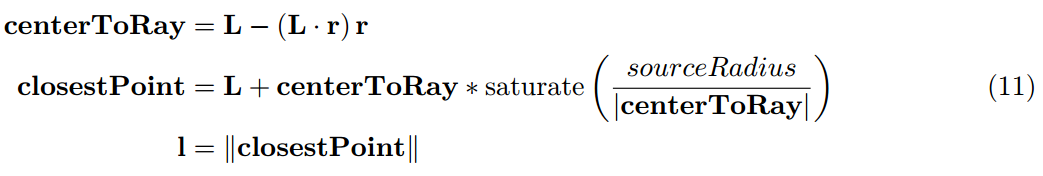
这里,L是从着色点到光源中心的向量,并且sourceRadius是灯光球体的半径,r是反射向量。在这个案例中,射线与球相交,计算点将会是射线到球体中心的最近点。一旦标准化,它就是相同的。
通过移动发射光的原点到球的表面,我们通过球的对角高效的拓宽了镜面反射分布。尽管它不是一个微表面的分布,这可以用标准化的Phong分布来解释。
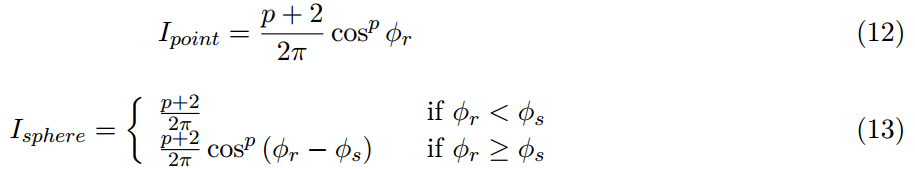
这里ϕr是r和L之间的夹角,并且ϕs是球对角的半角,Ipoint是标准化的,意味着积分的结果在半球上为1。Isphere显然不再标准化并取决于p的指数,积分可以大的多。

图11:用等式13解释的拓宽效应的可视化
为了近似能量上的增长,我应用先前描述的镜面反射修改相同的原由,我们基于光照的立体角拓宽了分布。我们使用标准化因子实现更广泛的分布并替换初始的标准化因子。对于GGX,标准化因子是1/πα2。为了对代表点操作推导一个近似的标准化,我们将新的拓宽的标准化因子除以初始的标准化因子:![]()
代表点方法的结果满足我们所有的需求。通过正确的处理能量守恒,无论光源大小如何,材质表现一致。光滑材质依然提供了锐利边缘的镜面反射高光,并且因为 它只是修改了BRDF的输入,我们的着色模型不被影响。最后,它足够高雄啊,允许我们的艺术家再任何地方使用。
灯管-Tube Lights
球形灯对于表现灯泡有帮助,灯管(胶囊)对于表现现实世界中相当广泛的荧光灯有帮助。开始,我们用一个长度但是半径为0,也被称为线性灯光来解决灯管。只要线段再水平线之上,线段的辐照度可以被解析地积分。
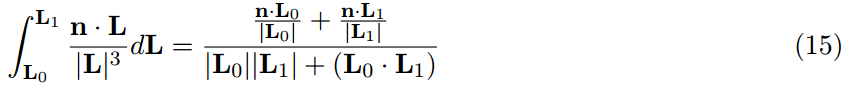
这里L0和L1是从着色点导线段终点的向量。

图12:左边为参考,右边是代表点方法。尽管能量守恒不完美,我们的近似值与参考值匹配得令人信服。
我们修改了这个方程式来防止辐照度为负值,除以0,并且当长度为0时匹配我们的点光衰减。
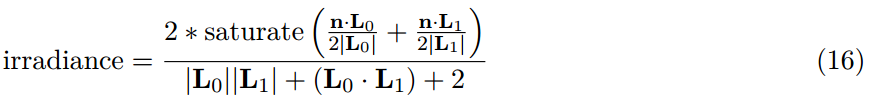
对于线性光镜面反射我们需要在下面的方程组里解出t:

Picott发现与r最小角的t的值:
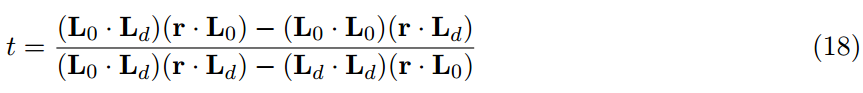
和球的案例相似,我们近似了最小角并且求解而不是为了最短距离:
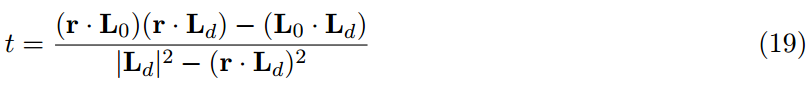
这会造成边界没有正常处理的情况,这样就不能总是找到最近点,但是这样计算起来成本略低,并且看起来提供了方程式18一样合理的结果。
注意,这是因为方程式18和19都把r视作一条线段而不是射线是重要的,解决方案都未能正确处理指向远离线段的射线。甚至对于完美的平面,这会造成从一个结束点到另一个结束点的生硬变化。我们通过在计算点和每一个结束点之间选择来解决这个问题,但是这样做成本较高。此时我们只好接受了这个瑕疵。
为了使能量守恒,我们应用了用于球形光的相同概念。镜面反射分布通过灯光的对角已经被拓宽,但是这次只是一维的,所以我们使用GGX的各向异性版本。各向异性GGX的标准化因子是1/παxαy,在各向同性案例中,这里αx=αy=α,这给了我们:
![]()
因为我们只改变了灯光的原点并应用了一个能量守恒项,这些操作可以被加速。用线段和球来做,近似形状的卷积并且很好的模拟了灯管的表现。灯管的结果展示在图13。

图13:使用能量守恒的代表点方法的灯管
我们已经发现能量守恒的代表点方法对于简单形状效率高,并且在未来,除了球形和管形之外,可能会应用在其他的形状。特别是,我们想要应用它到四方纹理来表现更复杂和多彩的光源。
结论
我们在着色,材质和灯光领域转向基于物理的实现,已经被正式非常的成功。在我们最近的《渗透者》demo的图形部分贡献极大,并且我们计划在未来所有的项目中使用这些实现。事实上,这些改变的可行部分已经集成进《堡垒之夜》,在这项工作开始之前便已经进展顺利的项目。我们打算在这些领域以实现更高的灵活性的目的继续提升,并且提升目标是各种场景和所有级别的硬件可以享受基于物理方法的好处的可扩展性。