java 数据结构与算法---二叉树

 原理来自百度百科     推荐数据演示网址 ：https://www.cs.usfca.edu/~galles/visualization/BST.html

一、什么是二叉树

 　　二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2的(i-1)次方个结点；深度为k的二叉树至多有2的k次方然后减1个结点(次方不会敲所以用文字描述)；对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。

二、二叉树的分类：

1、满二叉树：除叶子结点外的所有结点均有两个子结点。

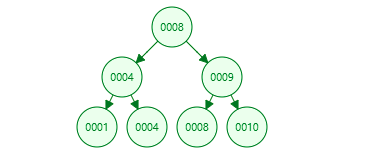
满二叉树的性质：
1) 一颗树深度为h，最大层数为k，深度与最大层数相同，k=h;
2) 树的第k层，则该层的叶子节点个数为2k;
3) 第k层的结点个数是2的(k-1)次方。
4) 总结点个数是2的k次方减1，且总节点个数一定是奇数。

2、完全二叉树：若设二叉树的深度为h，除第 h 层外，其它各层 (1～(h-1)层) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。

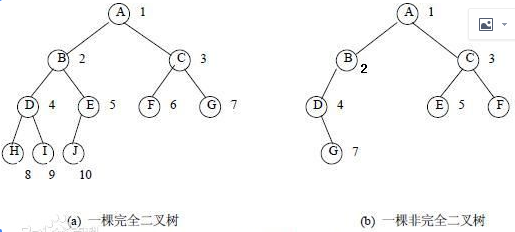
完全二叉树的特点是：
1）只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现；
2）对任一结点，如果其右子树的深度为j，则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个。

满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

三、二叉树在数据结构中的实现

二叉树在一般数据结构中是按照二叉排序树进行实现、使用的。二叉排序树（Binary Sort Tree）：又称二叉查找树（Binary Search Tree），亦称二叉搜索树。

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
（3）左、右子树也分别为二叉排序树；

1、二叉排序树节点的数据结构

private static class Node<E>{
        private E e;//当前节点的数据
        private Node<E> leftNode;//当前节点左子节点
        private Node<E> rightNode;//当前节点右子节点
        public Node(E e, Node<E> leftNode, Node<E> rightNode) {
            super();
            this.e = e;
            this.leftNode = leftNode;
            this.rightNode = rightNode;
        }    
    }

2、插入节点

如果是空树（不存在节点），则直接插入。
如果不是空树，则从根节点开始查找相应的节点，即查找新节点的父节点，当父节点找到后，根据新节点的值来确定新节点是在左节点上，还是右节点上。

    public void insert(E e) {
        Node<E> node=new Node<E>(e,null,null);
        if(root==null) {
            root=node;
        }else {
            Node<E> fNode=root;
            Node<E> parentNode=root;//要找的父节点
            while(true) {
                parentNode=fNode;
                if(compareToE(e,fNode.e)) {
                    fNode=fNode.leftNode;
                    if(fNode==null) {
                        parentNode.leftNode=node;
                        break;
                    }
                }else {
                    fNode=fNode.rightNode;
                    if(fNode==null) {
                        parentNode.rightNode=node;
                        break;
                    }
                }
                
            }
        }
        size++;
    }
    //只是实现了数值比较
    private boolean compareToE(E a,E b) {
        Integer a1=(Integer) a;
        Integer b1=(Integer) b;
        return a1<b1;
    }

3、查找节点

从根节点开始查找，如果要查找的节点值比父节点值小，则查左子节点，否则查右子节点，直到查到为止，如果不存在就返回null

    public Node<E> find(E e){
        if(root.e==e) {
            return root;
        }
        Node<E> fNode=root;
        while(true) {
            if(compareToE(e,fNode.e)) {
                fNode=fNode.leftNode;
            }else {
                if(fNode.e.equals(e)) {
                    return fNode;
                }
                fNode=fNode.rightNode;
            }
            if(fNode==null) {
                return null;
            }
        }
    }

 4、二叉树的遍历方式

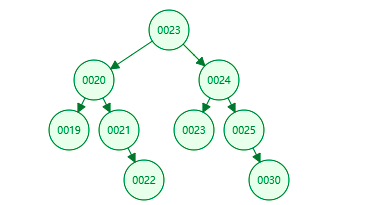
A、先序遍历    遍历规则 访问节点，访问该节点的左子树，访问该节点的右子树   23 ->20 ->24  （每一个节点都是该规则）

public void preTraversalTree(Node<E> node) {
        if(node!=null) {
            node.display();
            preTraversalTree(node.leftNode);
            preTraversalTree(node.rightNode);
        }
    }

结果： E:23 E:20 E:19 E:21 E:22 E:24 E:23 E:25 E:30

B、中序遍历：  遍历规则  先遍历左子树，然后该节点，最后遍历该节点右子树    20 ->23 ->24  （每一个节点都是该规则）

public void cenTraversalTree(Node<E> node) {
        if(node!=null) {
            cenTraversalTree(node.leftNode);
            node.display();
            cenTraversalTree(node.rightNode);
        }
    }

结果： E:19 E:20 E:21 E:22 E:23 E:23 E:24 E:25 E:30

C、后续遍历   遍历规则  先遍历左子树，然会遍历该节点右子树，最后该节点， 20 ->24 ->23  （每一个节点都是该规则）

public void aftTraversalTree(Node<E> node) {
        if(node!=null) {
            aftTraversalTree(node.leftNode);
            aftTraversalTree(node.rightNode);
            node.display();
            
        }
    }

 结果：   E:19 E:22 E:21 E:20 E:23 E:30 E:25 E:24 E:23

完整代码

package com.jalja.org.algorithm;


public class MyTree<E> {
    private Node<E> root;//根节点
    private int size=0;//树中节点的个数
    public MyTree() {
        
    }
    private static class Node<E>{
        private E e;//当前节点的数据
        private Node<E> leftNode;//当前节点左子节点
        private Node<E> rightNode;//当前节点右子节点
        public Node(E e, Node<E> leftNode, Node<E> rightNode) {
            super();
            this.e = e;
            this.leftNode = leftNode;
            this.rightNode = rightNode;
        }
        public void display() {
            System.out.print(" E:"+e);
        }        
    }
    //如果是空树（不存在节点），则直接插入。
    //如果不是空树，则从根节点开始查找相应的节点，即查找新节点的父节点，当父节点找到后，根据新节点的值来确定新节点是在左节点上，还是右节点上。
    public void insert(E e) {
        Node<E> node=new Node<E>(e,null,null);
        if(root==null) {
            root=node;
        }else {
            Node<E> fNode=root;
            Node<E> parentNode=root;//要找的父节点
            while(true) {
                parentNode=fNode;
                if(compareToE(e,fNode.e)) {
                    fNode=fNode.leftNode;
                    if(fNode==null) {
                        parentNode.leftNode=node;
                        break;
                    }
                }else {
                    fNode=fNode.rightNode;
                    if(fNode==null) {
                        parentNode.rightNode=node;
                        break;
                    }
                }
                
            }
        }
        size++;
    }
    //只是实现了数值比较
    private boolean compareToE(E a,E b) {
        Integer a1=(Integer) a;
        Integer b1=(Integer) b;
        return a1<b1;
    }
    //从根节点开始查找，如果要查找的节点值比父节点值小，则查左子节点，否则查右子节点，直到查到为止，如果不存在就返回null
    public Node<E> find(E e){
        if(root.e==e) {
            return root;
        }
        Node<E> fNode=root;
        while(true) {
            if(compareToE(e,fNode.e)) {
                fNode=fNode.leftNode;
            }else {
                if(fNode.e.equals(e)) {
                    return fNode;
                }
                fNode=fNode.rightNode;
            }
            if(fNode==null) {
                return null;
            }
        }
    }
    public void preTraversalTree(Node<E> node) {
        if(node!=null) {
            node.display();
            preTraversalTree(node.leftNode);
            preTraversalTree(node.rightNode);
        }
    }
    
    public void cenTraversalTree(Node<E> node) {
        if(node!=null) {
            cenTraversalTree(node.leftNode);
            node.display();
            cenTraversalTree(node.rightNode);
        }
    }
    
    public void aftTraversalTree(Node<E> node) {
        if(node!=null) {
            aftTraversalTree(node.leftNode);
            aftTraversalTree(node.rightNode);
            node.display();
            
        }
    }
    
    
    public static void main(String[] args) {
        MyTree<Integer> myTree=new MyTree<Integer>();
        myTree.insert(23);
        myTree.insert(20);
        myTree.insert(24);
        myTree.insert(19);
        myTree.insert(21);
        myTree.insert(23);
        myTree.insert(25);
        myTree.insert(22);
        myTree.insert(30);
        myTree.aftTraversalTree(myTree.find(23));
    }
    
}