一、概念
数据排序 :排序就是将一组对象按照规定的次序重新排列的过程,排序往往是为检索服务的。
稳定排序 :若排序后,相同关键字的记录保持它们原来的相对次序,则此排序方法称为稳定排序;稳定性是排序方法本身的特性,与数据无关。
排序类型:
- 内部排序: 全部数据存于内存;
- 外部排序: 需要对外存进行访问的排序过程
排序指标(排序算法性能分析):
- 存储空间
- 比较次数
二、插入排序
常用的插入排序方法有直接插入排序、折半插入排序、表插入排序和希尔排序。
直接插入排序(Straight Insertion Sorting)是一种简单的排序方法,它的基本思想是依次将每个记录插入到一个已排好序的有序表中去,从而得到一个新的、记录数增加 1 的有序表。直接插入排序类似图书馆中整理图书的过程。
// R 待排序的表 n是表长 void StraightlnsertSort(List R,int n){ int i,j; for (i=2;i<=n;i++){ R[0]=R[i];//第 i 个记录复制为岗哨 j=i-1; while (R[0].key<R[j].key){ //与岗哨比较,直至键值不大于岗哨键值 R[j+1]=R[j]; //将第 j 个记录赋值给第 j+1 个记录 j--; } R[j+1]=R[0]; //将第 i 个记录插入到序列中 } }
记录 R[0]有两个作用,其一是进入查找循环之前,它保存了 R[i]的值,使得不致于因 记录的后移而丢失 R[i]中的内容;其二是起岗哨作用,在 while 循环中“监视”数组下标 变量 j 是否越界,一旦越界(即 j<1), R[0]自动控制 while 循环的结束,从而避免了在 while 循环中每一次都要检测 j 是否越界。这一技巧的应用,使得测试循环条件的时间大 约减少一半。
算法分析:直接插入排序的算法简单,易于理解,容易实现,时间复杂度为 O(n2 ),若待排序记录 的数量很大时,一般不选用直接插入排序。从空间来看,它只需要一个记录的辅助空间,即 空间复杂度为 O(1)。 直接插入排序方法是稳定的。
●存储空间 n+1;(1为附加空间),空间复杂度 O(1)
●时间复杂度 O(n^ 2) ,如果给出的待排序表是顺序的,则时间复杂度最好 O(n)
●稳定性:稳定排序;


三、交换排序
交换排序的基本思想:比较两个记录键值的大小,如果这两个记录键值的大小出现逆 序,则交换这两个记录,这样将键值较小的记录向序列前部移动,键值较大的记录向序列 后部移动。
交换排序包括:冒泡排序和快速排序。
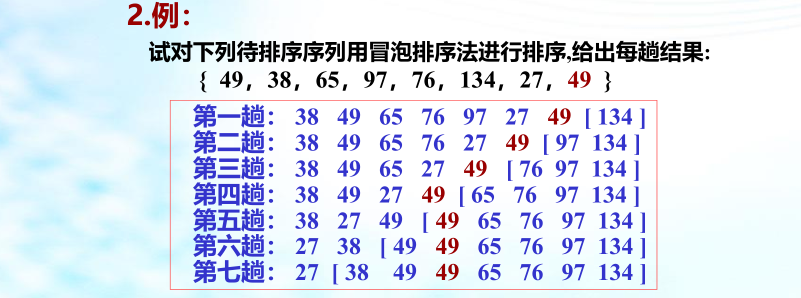
1、冒泡排序:
基本思想: 通过多次重复比较、交换相邻记录而实现排序;每一趟的效果都是将当前键值最大的记录换到最后
在算法实现时,定义一个整型变量 endsort,在每一次排序之前,先将它置为 0,若 在一趟起泡中交换了记录,则将它置为 1。当一次循环结束时,我们再检查 endsort,若 endsort 的值为 0 便终止算法。
// R 待排序的表 n是表长 void BubbleSort(List R,int n){ /*endsort:标志文件是否已排好序*/ for( i=1; i<=n-1; i++ ){ endsort=0; /*若循环中记录未作交换,则说明序列已有序*/ for( j=1; j<=n-i-1; j++ ){ if( R[j].key > R[j+1].key ){ temp=R[j]; R[j]=R[j+1]; R[j+1]=temp; endsort=1; } } if(endsort==0) break; } }
- 时间复杂度: O(n2 ) 、如果是排好序的表 O(n)
- 空间复杂度 :O(1)
- 稳定性:稳定排序。
2、快速排序(Quick Sorting)是交换排序的一种,实质上是对冒泡排序的一种改进;首先取第一个记录,将之与表中其余记录比较并交换,从而将它放到记录的正确的最终位置,使记录表分成两部分{其一(左边的)诸记录的关键字均小于它;其二(右边的)诸记录的关键字均大于它};然后对这两部分重新执行上述过程,依此类推,直至排序完毕


四、选择排序
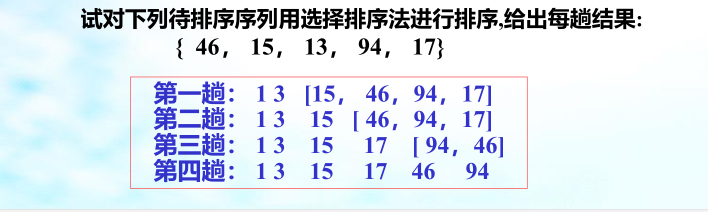
选择排序(Selection Sorting)的基本思想:每一次在 n-i+1(i=1,2,…,n-1)个记录中 选取键值最小的记录作为有序序列的第 i 个记录。
分类:直接选择排序和堆排序
1.直接选择排序
直接选择排序算法的基本思想:在第 i 次选择操作中,通过 n-i 次键值间比较,从 n-i+1个记录中选出键值最小的记录,并和第 i(1≤i≤n-l)个记录交换。
void SelectSort (List R,int n){ int min,i,j; //每次循环,选择出一个最小键值 for(i=1;i<=n-1;i++){ min=i; //假设第 i 个记录键值最小 for (j=i+1;j<=n;j++){ if (R[j].key<R[min].key){ min=j;//记录下键值较小记录的下标 }
}; if (min!=i){ swap(R[min],R[i]); //将最小键值记录和交换第 i 个记录交换 } } }

2、堆排序
建堆(筛选法):
- 1)方法:
- 设记录{ R 1 , R 2 , …., R n }
- (1)顺序输入成完全二叉树(以数组存储)
- (2)从最后一个双亲开始,如果有较小的孩子,则将其沿左或右孩中小的那个方向筛下,一直到不能再筛;
- (3)逐次处理完每个双亲。
对排序的特点:
- 在堆排序中,对于 n 个记录进行序所需的平均时间是 O(nlog2n)。
- 在最坏情况下,其 时间复杂度也为 O(nlog2n)。
- 相对于快速排序来说,这是堆排序的最大优点。
- 堆排序 仅需一个记录大小的供交换用的辅助存储空间。O(1)
- 堆排序是不稳定的。

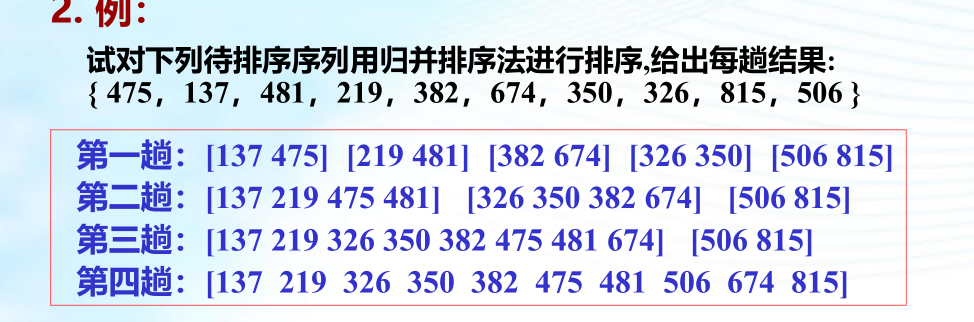
五、归并排序
归并排序(Merge Sorting)是与插入排序、交换排序、选择排序不同的一类排序方法,其不 同之处在于要求待排序列是由若干个有序子序列组成。归并的含义是将两个或两个以上的有 序表合并成一个新的有序表。合并的方法是比较各子序列的第一个记录的键值,最小的一个 就是排序后序列的第一个记录的键值。取出这个记录,继续比较各子序列现有的第一个记录 的键值,便可找出排岸后的第二个记录。如此继续下去,最终可以得到排序结果。 因此归并排序的基础是合并。
分类:
- 有序序列的合并
- 二路归并排序
归并排序算法的时间复杂度为 O(nlog2n),由于要用到和待排记录等数量的数组 b 来存放结 果,所以实现归并排序需要附加一倍的存储开销。二路归并排序是稳定的。在 n 较大时,归并排序的时间性能优于堆排序,但它所需的辅助存储量较多。O(n)