程序员，你心里需要有点树

看官，不要生气，我没有骂你也没有鄙视你的意思，今天就是想单纯的给大伙分享一下树的相关知识，但是我还是想说作为一名程序员，自己心里有没有点树？你会没点数吗？言归正传，树是我们常用的数据结构之一，树的种类很多有二叉树、二叉查找树、平衡二叉树、红黑树、B树、B+树等等，我们今天就来聊聊二叉树相关的树。

什么是树?

首先我们要知道什么是树？我们平常中的树是往上长有分支的而却不会形成闭环，数据结构中的树跟我们我们平时看到的树类似，确切的说是跟树根长得类似，我画了一幅图，让大家更好的理解树。

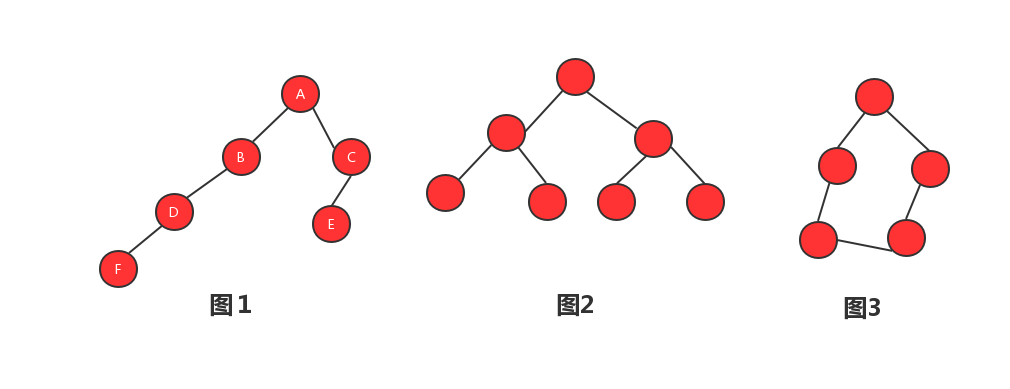
图１、图２都是树，图３不是树。每个红色的圆圈我们称之为元素也叫节点，用线将两个节点连接起来，这两个节点就形成了父子关系,同一个父节点的子节点成为兄弟节点，这跟我们家族关系一样，同一个父亲的叫做兄弟姐妹，在家族里面最大的称为老子，树里面也是一样的，只是不叫老子，叫做跟节点，没有子节点的叫做叶子节点。我们拿图１来做示例，A为根节点，B、C为兄弟节点，E、F为叶子节点。

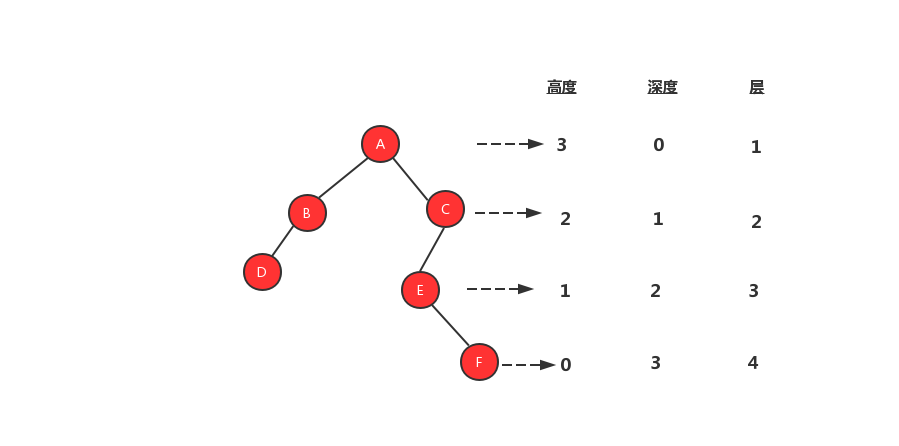
一颗树还会涉及到三个概念高度、深度、层，我们先来看看这三个名词的定义：

高度：节点到叶子节点的最长路径，从０开始计数

深度：跟节点到这个节点所经历的边数，从０开始计数

层：节点距离根节点的距离，从１开始计数

知道了三个名词的概念之后，我们用一张图来更加形象的表示这三个概念。

以上就是树的基本概念，树的种类很多，我们主要来学学二叉树。

二叉树

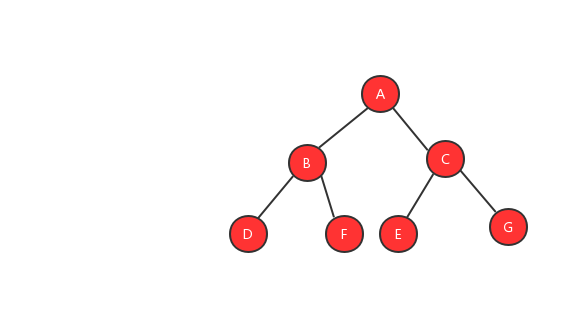
二叉树就像它的名字一样，每个元素最多有两个节点，分别称为左节点和右节点。当然并不是每个元素都需要有两个节点，有的可能只有左节点，有的可能只有右节点。就像国家开放二胎一样，也不是每个人都需要生两个孩子。下面我们来看看一颗典型的二叉树。

基于树的存储模式的不同，为了更好的利用存储空间，二叉树又分为完全二叉树和非完全二叉树，我们先来看看什么是完全二叉树、非完全二叉树？

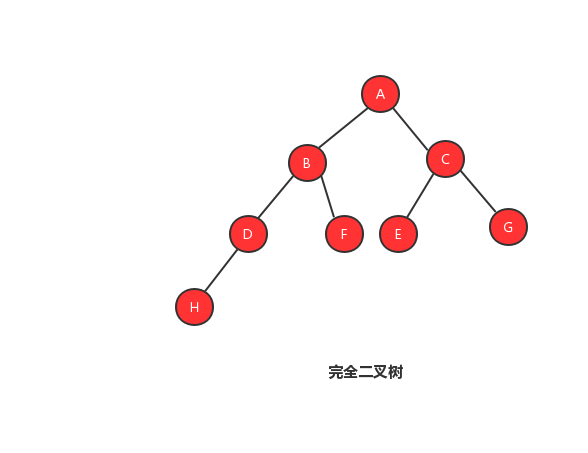
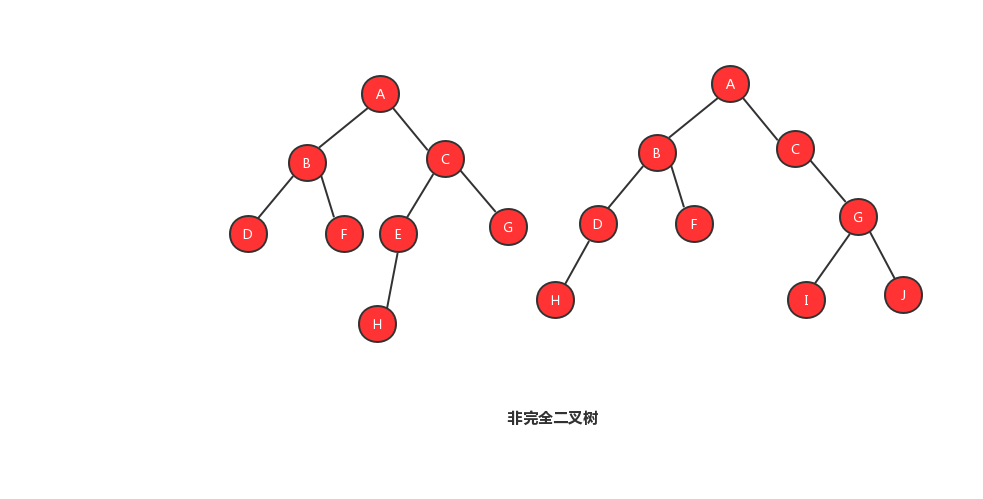
完全二叉树的定义：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大

也许单看定义会看不明白，我们来看几张图，你就能够明白什么是完全二叉树、非完全二叉树。

１、完全二叉树

２、非完全二叉树

上面我们说了基于树的存储模式不同，而分为完全二叉树和非完全二叉树，那我们接下来来看看树的存储模式。

二叉树的存储模式

二叉树的存储模式有两种，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法

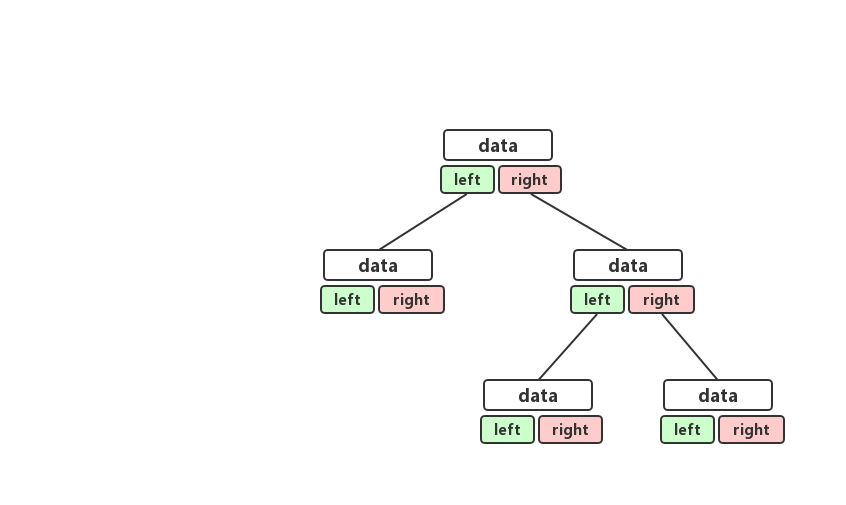
二叉链式存储法

链式存储法相对比较简单，理解起来也非常容易，每一个节点都有三个字段，一个字段存储着该节点的值，另外两个字段存储着左右节点的引用。我们顺着跟字节就可以很轻松的把整棵树串起来，链式存储法的结构大概长成这样。

顺序存储法

顺序存储法是基于数组实现的，数组是一段有序的内存空间，如果我们把跟节点的坐标定位i=1，左节点就是 2 * i = 2，右节点 2 * i+ 1 = 3，以此类推，每个节点都这么算，然后就将树转化成数组了，反过来，按照这种规则我们也能将数组转化成一棵树。看到这里我想你一定看出了一些弊端， 如果这是一颗不平衡的二叉树是不是会造成大量的空间浪费呢？没错，这就是为什么需要分完全二叉树和非完全二叉树。分别来看看这两种树基于数组的存储模式。

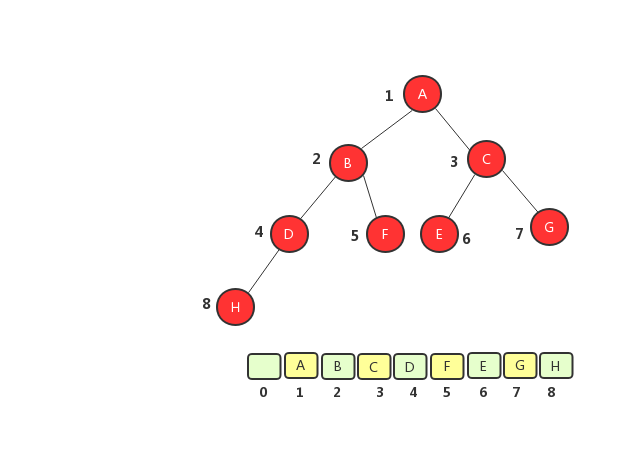
完全二叉树顺序存储法

非完全二叉树顺序存储法

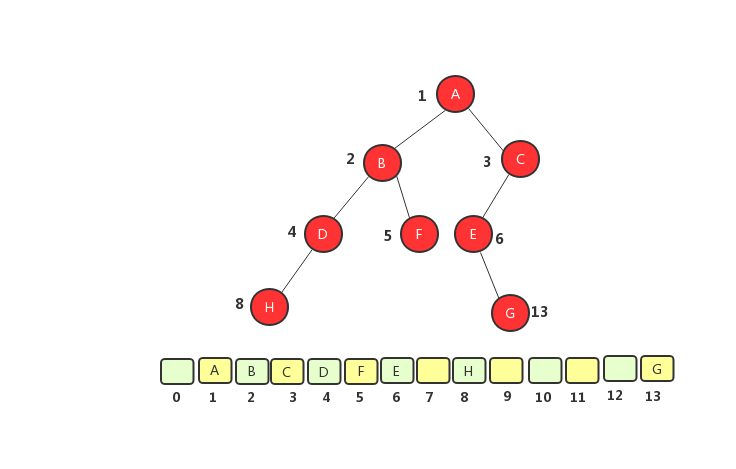
从图中将树转化成数组之后可以看出，完全二叉树用数组来存储只浪费了一个下标为0的存储空间，二非完全二叉树则浪费了大量的空间。如果树为完全二叉树，用数组存储比链式存储节约空间，因为数组存储不需要存储左右节点的信息

上面我们了解了二叉树的定义、类型、存储方式，接下来我们一起了解一下二叉树的遍历，二叉树的遍历也是面试中经常遇到的问题。

二叉树遍历

要了解二叉树的遍历，我们首先需要实例化出一颗二叉树，我们采用链式存储的方式来定义树，实例化树需要树的节点信息，用来存放该节点的信息，因为我们才用的是链式存储，所以我们的节点信息如下。

/**
 * 定义一棵树
 */
public class TreeNode {
    // 存储值
    public int data;
    // 存储左节点
    public TreeNode left;
    // 存储右节点
    public TreeNode right;

    public TreeNode(int data) {
        this.data = data;
    }
}

定义完节点信息之后，我们就可以初始化一颗树啦，下面是初始化树的过程:

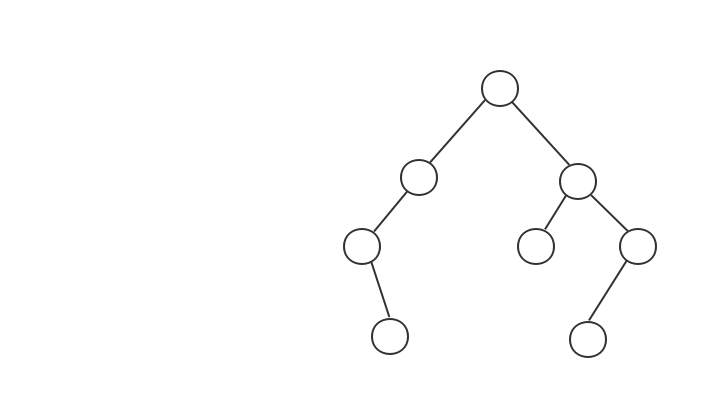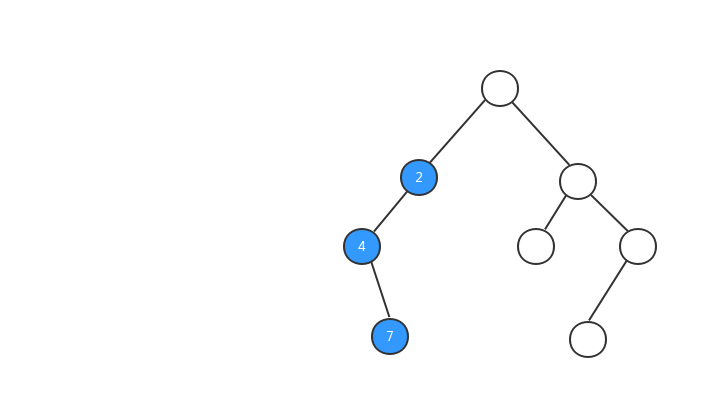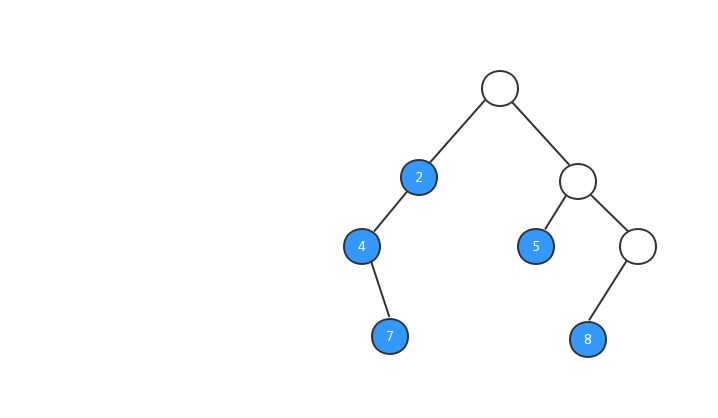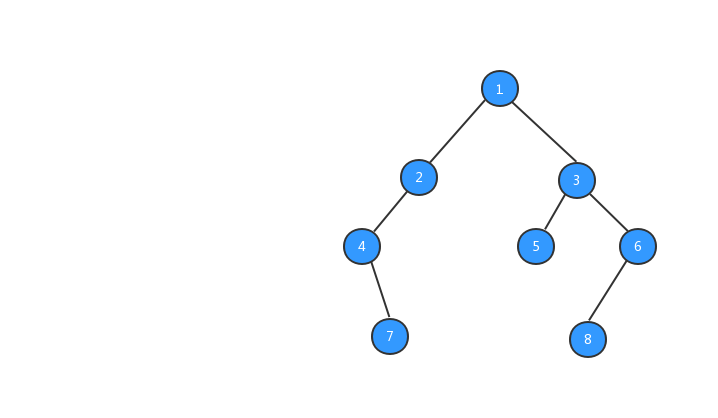
public static TreeNode buildTree() {
    // 创建测试用的二叉树
    TreeNode t1 = new TreeNode(1);
    TreeNode t2 = new TreeNode(2);
    TreeNode t3 = new TreeNode(3);
    TreeNode t4 = new TreeNode(4);
    TreeNode t5 = new TreeNode(5);
    TreeNode t6 = new TreeNode(6);
    TreeNode t7 = new TreeNode(7);
    TreeNode t8 = new TreeNode(8);

    t1.left = t2;
    t1.right = t3;
    t2.left = t4;
    t4.right = t7;
    t3.left = t5;
    t3.right = t6;
    t6.left = t8;

    return t1;
}

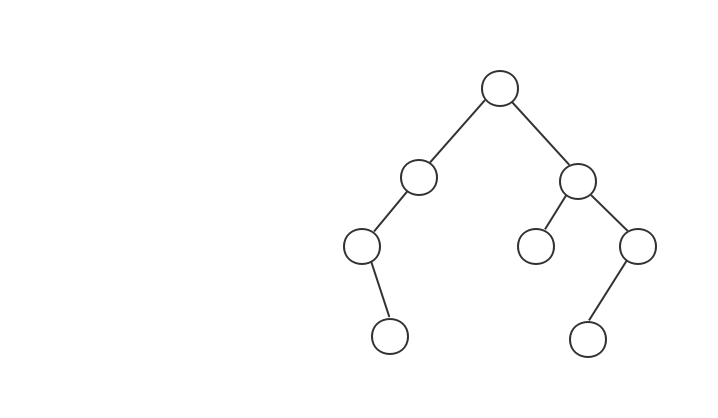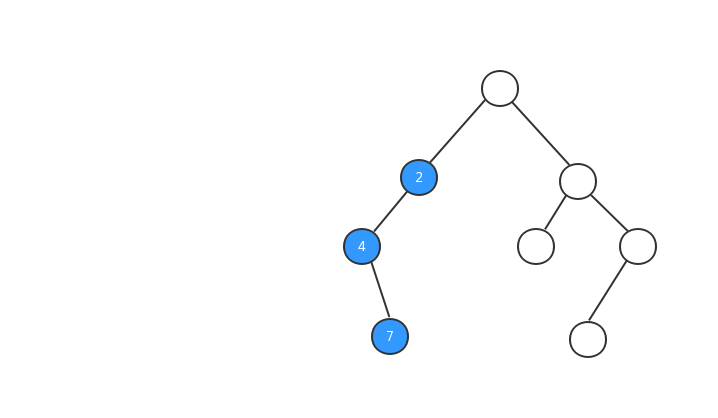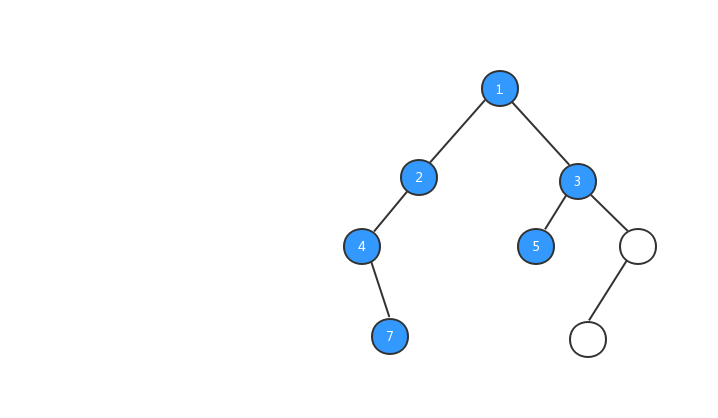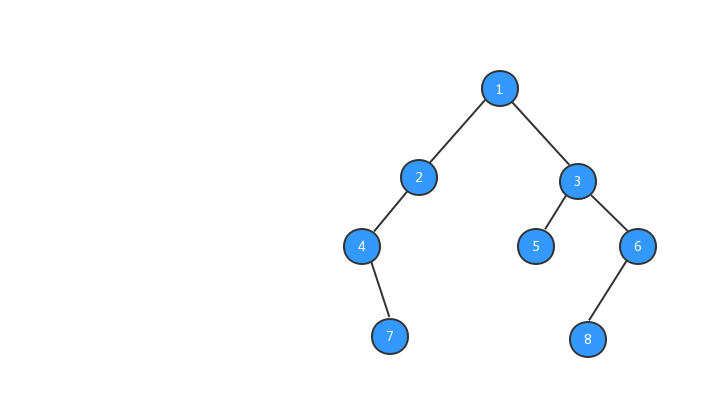
经过上面步骤之后，我们的树就长成下图所示的样子，数字代表该节点的值。

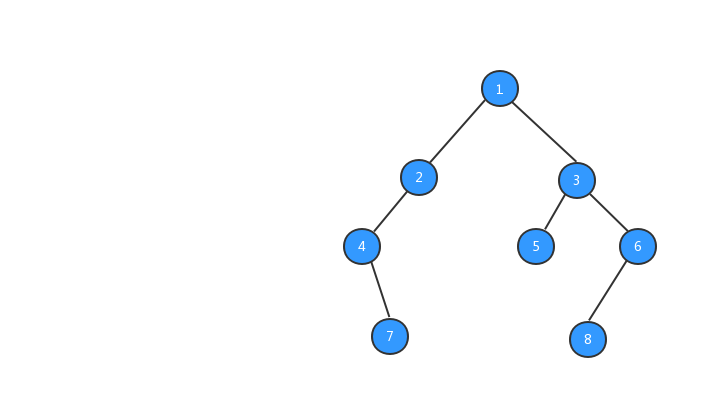
有了树之后，我们就可以对树进行遍历啦，二叉树的遍历有三种方式，前序遍历、中序遍历、后续遍历三种遍历方式，三种遍历方式与节点输出的顺序有关系。下面我们分别来看看这三种遍历方式。

前序遍历

前序遍历：对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。

为了方便大家的理解，我基于上面我们定义的二叉树，对三种遍历方式的执行流程都制作了动态图，希望对你的阅读有所帮助，我们先来看看前序遍历的执行流程动态图。

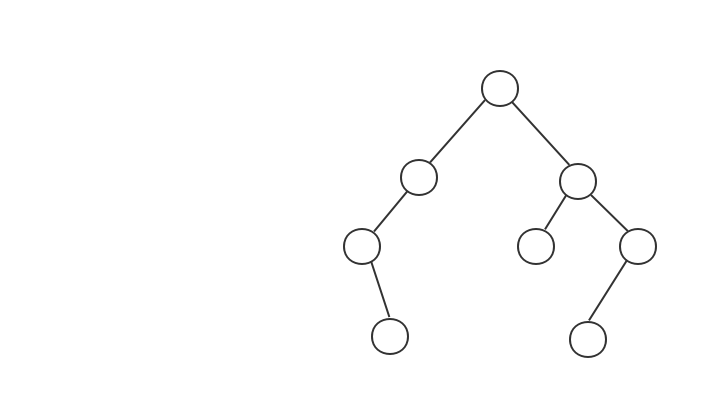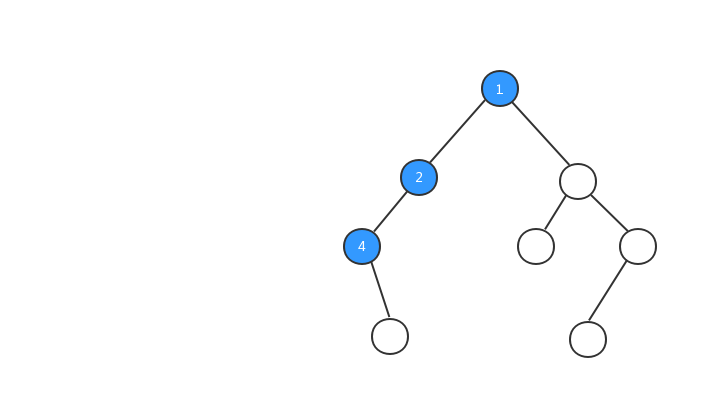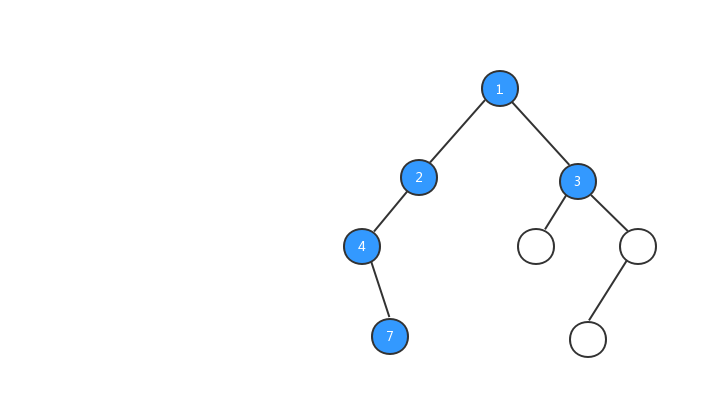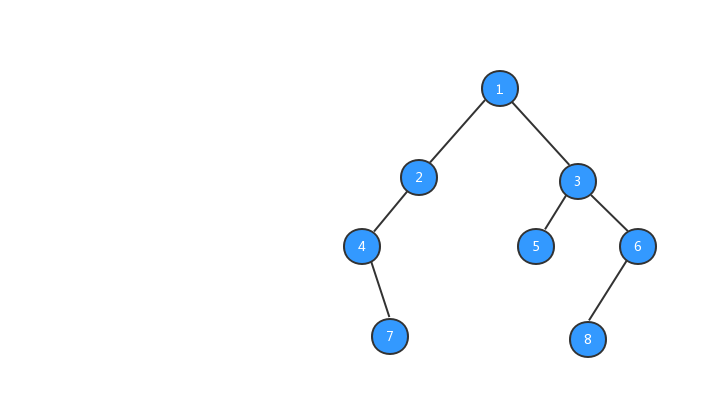
理解了前序遍历的概念和看完前序遍历执行流程动态图之后，你心里一定很想知道，在代码中如何怎么实现树的前序遍历？二叉树的遍历非常简单，一般都是采用递归的方式进行遍历，我们来看看前序遍历的代码：

// 先序遍历，递归实现 先打印本身，再打印左节点，在打印右节点
public static void preOrder(TreeNode root) {

    if (root == null) {
        return;
    }
    // 输出本身
    System.out.print(root.data + " ");
    // 遍历左节点
    preOrder(root.left);
    // 遍历右节点
    preOrder(root.right);
}

中序遍历

中序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。

跟前序遍历一样，我们来看看中序遍历的执行流程动态图。

中序遍历的代码：

// 中序遍历 先打印左节点，再输出本身，最后输出右节点
public static void inOrder(TreeNode root) {
    if (root == null) {
        return;
    }
    inOrder(root.left);
    System.out.print(root.data + " ");
    inOrder(root.right);
}

后序遍历

后序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

跟前两种遍历一样，理解概念之后，我们还是先来看张图。

后序遍历的实现代码：

// 后序遍历 先打印左节点，再输出右节点，最后才输出本身
public static void postOrder(TreeNode root) {
    if (root == null) {
        return;
    }
    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.data + " ");
}

二叉树的遍历还是非常简单的，虽然有三种遍历方式，但都是一样的，只是输出的顺序不一样而已，经过了上面这么多的学习，我相信你一定对二叉树有不少的认识，接下来我们来了解一种常用而且比较特殊的二叉树：二叉查找树

二叉查找树

二叉查找树又叫二叉搜索树，从名字中我们就能够知道，这种树在查找方面一定有过人的优势，事实确实如此，二叉查找树确实是为查找而生的树，但是它不仅仅支持快速查找数据，还支持快速插入、删除一个数据。那它是怎么做到这些的呢？我们先从二叉查找树的概念开始了解。

二叉查找树：在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。

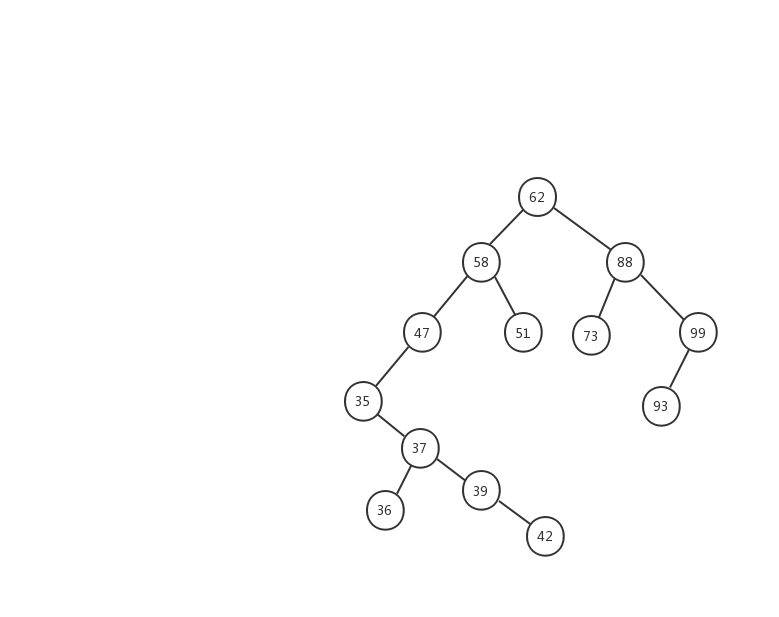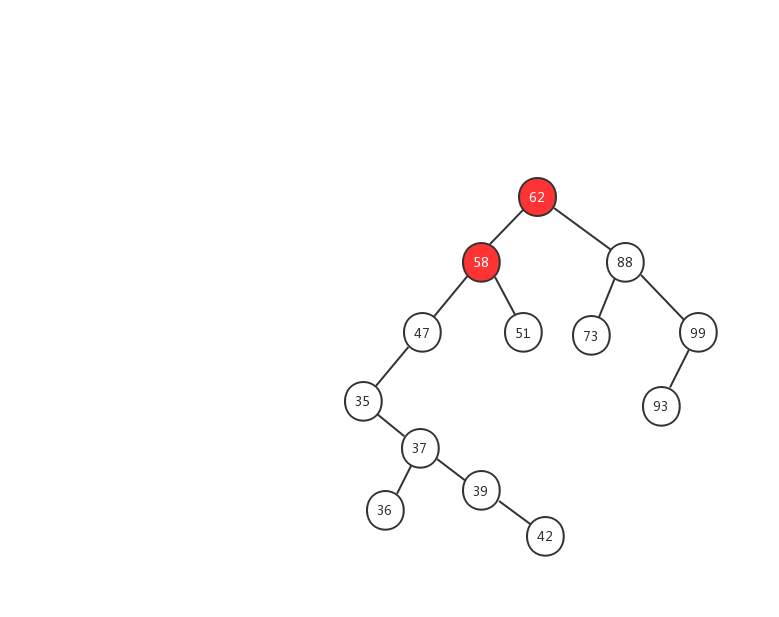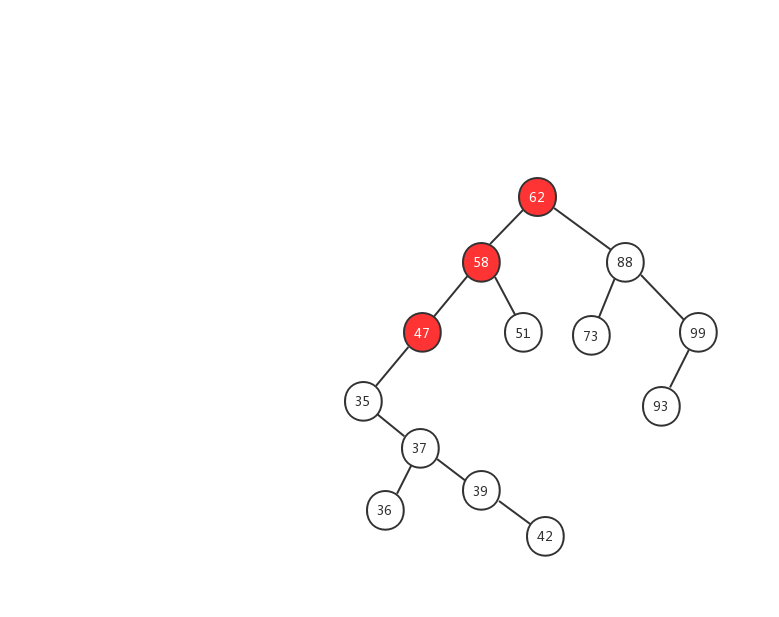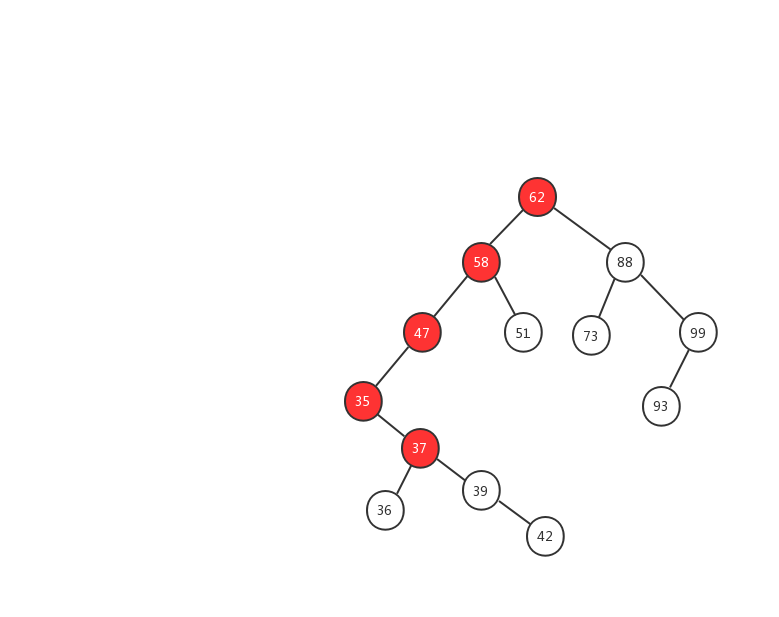
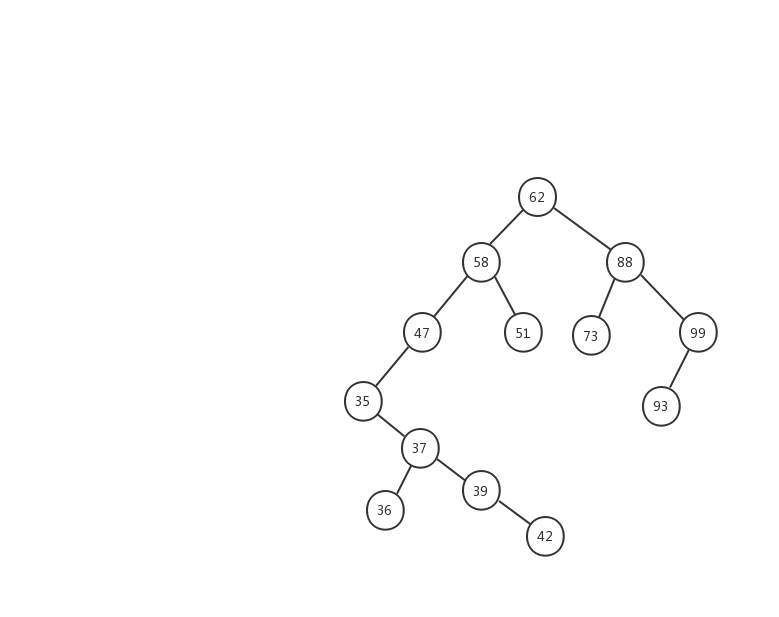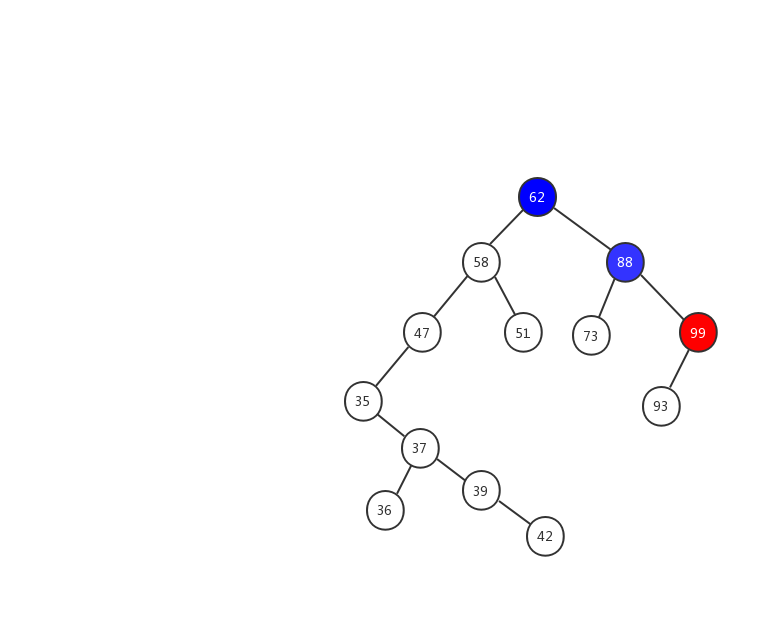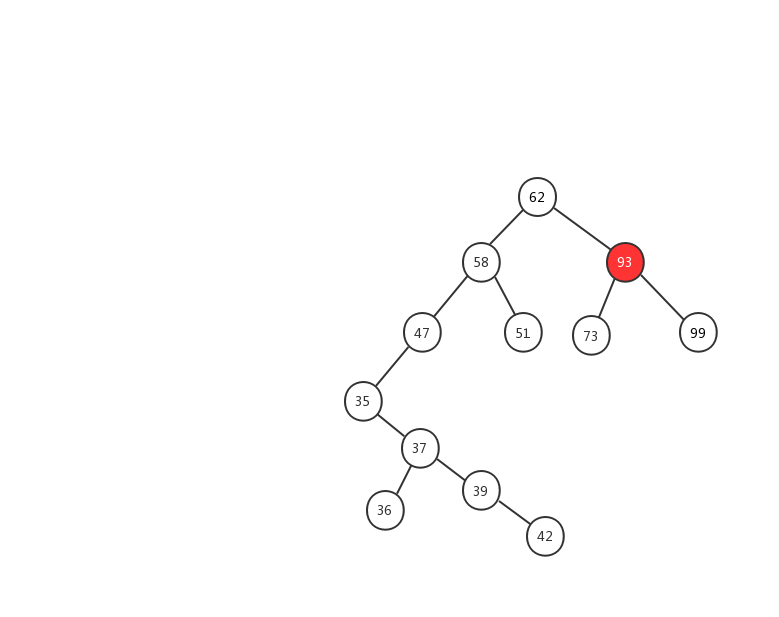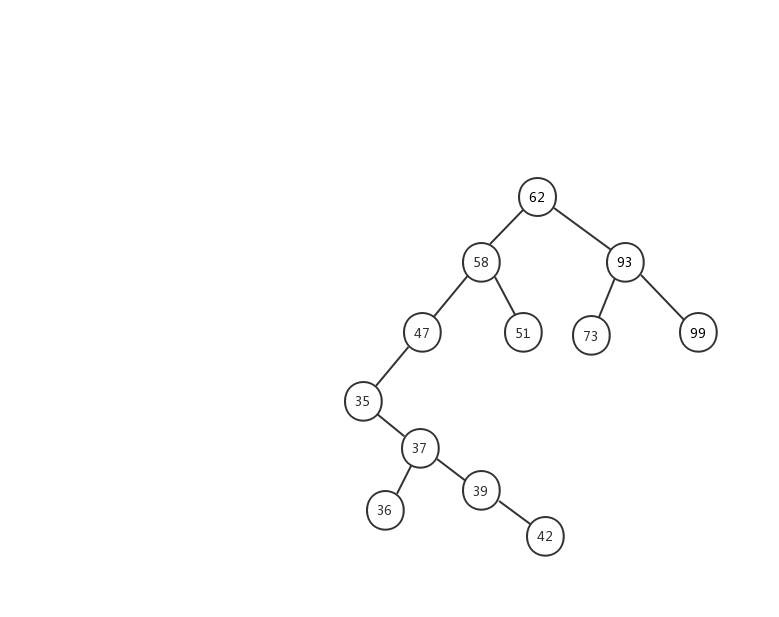
难以理解？记不住？没关系的，下面我定义了一颗二叉查找树，我们对着树，来慢慢理解。

根据二叉查找树的定义，每棵树的左节点的值要小于这父节点，右节点的值要大于父节点。62节点的 所有左节点的值都要小于 62 ，所有右节点 的值都要大于 62 。对于这颗树上的每一个节点都要满足这个条件，我们拿我们树上的另一个节点 35 来说，它的右子树上的节点值最大不能超过 47 ，因为 35 是 47 的左子树，根据二叉搜索树的规则，左子树的值要小于节点值。

二叉查找树既然名字中带有查找两字，那我们就从二叉查找树的查找开始学习二叉查找树吧。

二叉查找树的查找操作

由于二叉查找树的特性，我们需要查找一个数据，先跟跟节点比较，如果值等于跟节点，则返回根节点，如果小于根节点，则必然在左子树这边，只要递归查找左子树就行，如果大于，这在右子树这边，递归右子树即可。这样就能够实现快速查找，因为每次查找都减少了一半的数据，跟二分查找有点相似，快速插入、删除都是居于这个特性实现的。

下面我们用一幅动态图来加强对二叉查找树查找流程的理解，我们需要在上面的这颗二叉查找树中找出值等于 37 的节点，我们一起来看看流程图是怎么实现的。

• 1、先用 37 跟 62 比较，37 < 62 ，在左子树中继续查找
• ２、左子树的节点值为 58，37 < 58 ，继续在左子树中查找
• ３、左子树的节点值为 47，37 < 47，继续在左子树中查找
• ４、左子树的节点值为 35，37 > 35，在右子树中查找
• ５、右子树中的节点值为 37，37 = 37 ，返回该节点

讲完了查找的概念之后，我们一起来看看二叉查找树的查找操作的代码实现

/**
 * 根据值查找树
 * @param data　值
 * @return
 */
public TreeNode find(int data) {
    TreeNode p = tree;
    while (p != null) {
        if (data < p.data) p = p.left;
        else if (data > p.data) p = p.right;
        else return p;
    }
    return null;
}

二叉查找树的插入操作

插入跟查找差不多，也是从根节点开始找，如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。

假设我们要插入 63 ，我们用一张动态图来看看插入的流程。

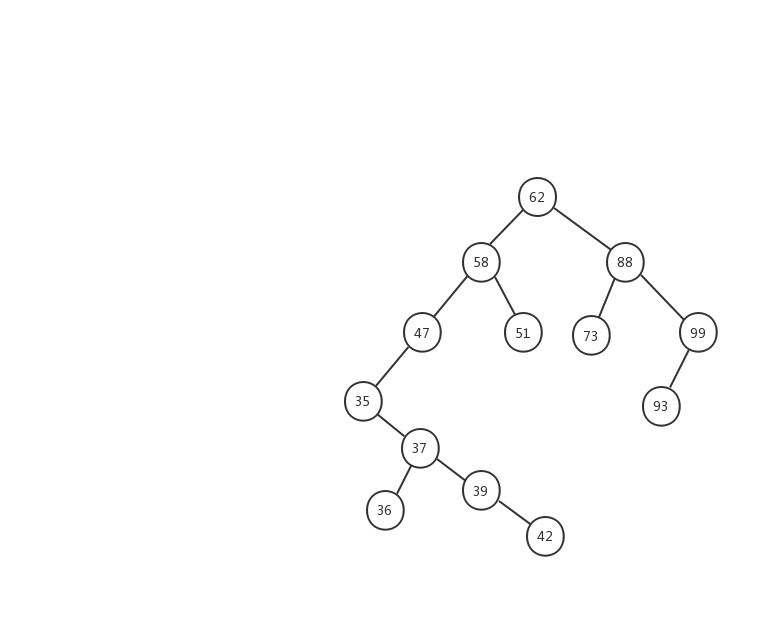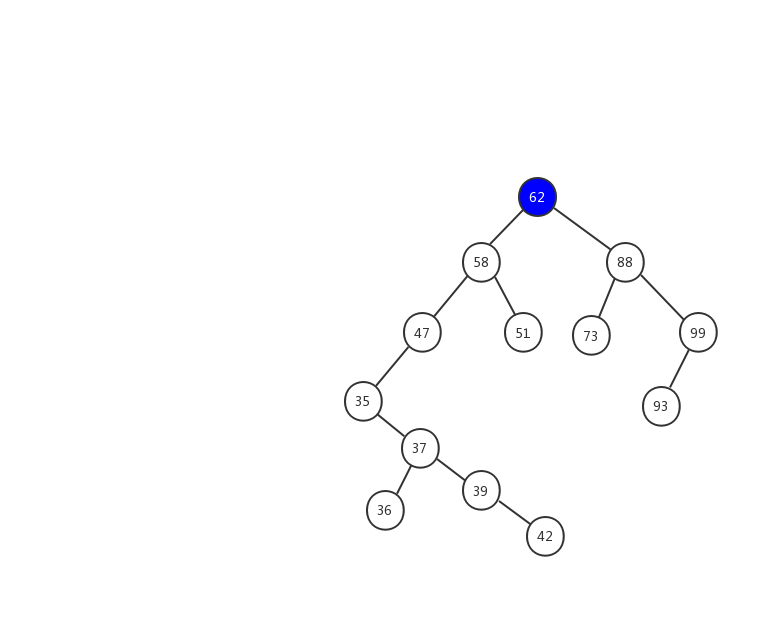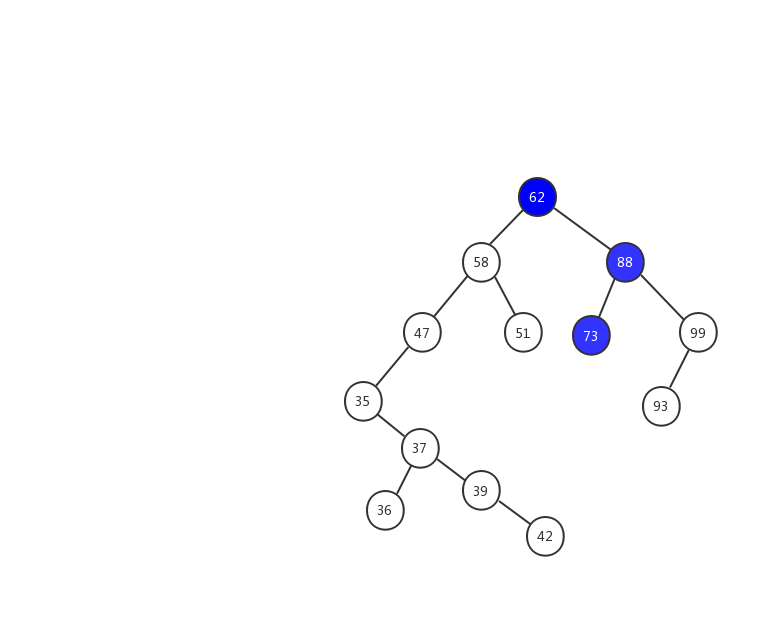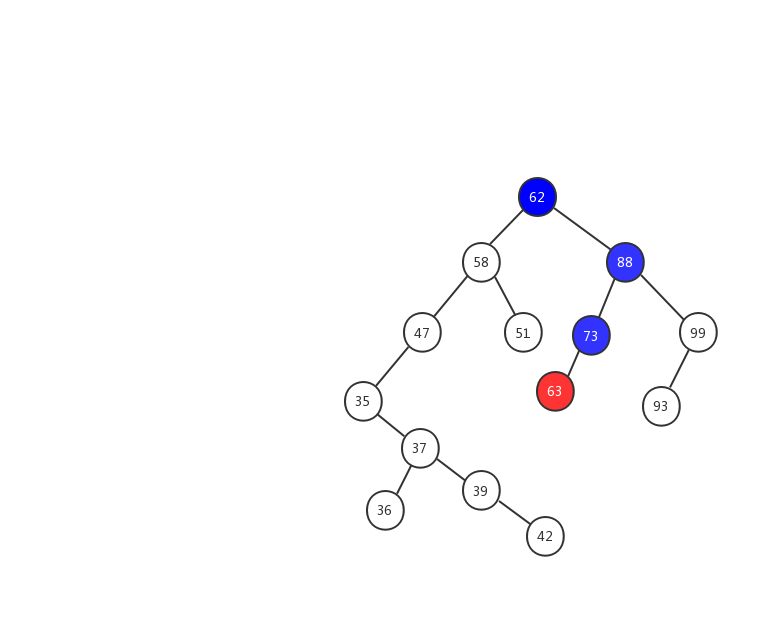
• 1、63 > 62 ，在树的右子树继续查找.
• 2、63 < 88 ，在树的左子树继续查找
• 3、63 < 73 ,因为 73 是叶子节点，所以 63 就成为了 73 的左子树。

我们来看看二叉查找树的插入操作实现代码

/**
 * 插入树
 * @param data
 */
public void insert(int data) {
    if (tree == null) {
        tree = new TreeNode(data);
        return;
    }

    TreeNode p = tree;

    while (p != null) {
        // 如果值大于节点的值，则新树为节点的右子树
        if (data > p.data) {
            if (p.right == null) {
                p.right = new TreeNode(data);
                return;
            }
            p = p.right;
        } else { // data < p.data
            if (p.left == null) {
                p.left = new TreeNode(data);
                return;
            }
            p = p.left;
        }
    }
}

二叉查找树的删除操作

删除的逻辑要比查找和插入复杂一些，删除分一下三种情况：

第一种情况：如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的指针置为 null。比如图中的删除节点 51。

第二种情况：如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。比如图中的删除节点 35。

第三种情况：如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 88

前面两种情况稍微简单一些，第三种情况，我制作了一张动态图，希望能对你有所帮助。

我们来看看二叉查找树的删除操作实现代码

public void delete(int data) {
    TreeNode p = tree; // p指向要删除的节点，初始化指向根节点
    TreeNode pp = null; // pp记录的是p的父节点
    while (p != null && p.data != data) {
        pp = p;
        if (data > p.data) p = p.right;
        else p = p.left;
    }
    if (p == null) return; // 没有找到

    // 要删除的节点有两个子节点
    if (p.left != null && p.right != null) { // 查找右子树中最小节点
        TreeNode minP = p.right;
        TreeNode minPP = p; // minPP表示minP的父节点
        while (minP.left != null) {
            minPP = minP;
            minP = minP.left;
        }
        p.data = minP.data; // 将minP的数据替换到p中
        p = minP; // 下面就变成了删除minP了
        pp = minPP;
    }

    // 删除节点是叶子节点或者仅有一个子节点
    TreeNode child; // p的子节点
    if (p.left != null) child = p.left;
    else if (p.right != null) child = p.right;
    else child = null;

    if (pp == null) tree = child; // 删除的是根节点
    else if (pp.left == p) pp.left = child;
    else pp.right = child;
}

我们上面了解了一些二叉查找树的相关知识，由于二叉查找树在极端情况下会退化成链表，例如每个节点都只有一个左节点，这是时间复杂度就变成了O(n)，为了避免这种情况，又出现了一种新的树叫平衡二叉查找树，由于本文篇幅有点长了，相信看到这里的各位小伙伴已经有点疲惫了，关于平衡二叉查找树的相关知识我就不在这里介绍了。

最后

打个小广告，金九银十跳槽季，平头哥给大家整理了一份较全面的 Java 学习资料，欢迎扫码关注微信公众号：「平头哥的技术博文」领取，祝各位升职加薪。