数据分析基础之Linalg的使用

Linear algebra

 

简介

When SciPy is built using the optimized ATLAS LAPACK and BLAS libraries, it has very fast linear algebra capabilities.

If you dig deep enough, all of the raw lapack and blas libraries are available for your use for even more speed.

All of these linear algebra routines expect an object that can be converted into a 2-dimensional array. The output of these routines is also a two-dimensional array.

1.模块文档

 

2.可用方法

'bench','cholesky','cond','det','division','eig','array','eigh','eigvals','eigvalsh','info','inv','lapack_lite','linalg','lstsq','matrix_power','matrix_rank','multi_dot','norm','pinv','print_function','qr','slogdet','solve','svd','tensorinv','tensorsolve','test'

eig : eigenvalues and right eigenvectors of general arrays
eigvalsh : eigenvalues of symmetric or Hermitian arrays.
eigh : eigenvalues and eigenvectors of symmetric/Hermitian arrays.

 

3.常用方法

首先导入相关模块

import numpy as np
from scipy import linalg as LA
#or
#from numpy import linalg as LA

3.1求数组的行列式：det

 

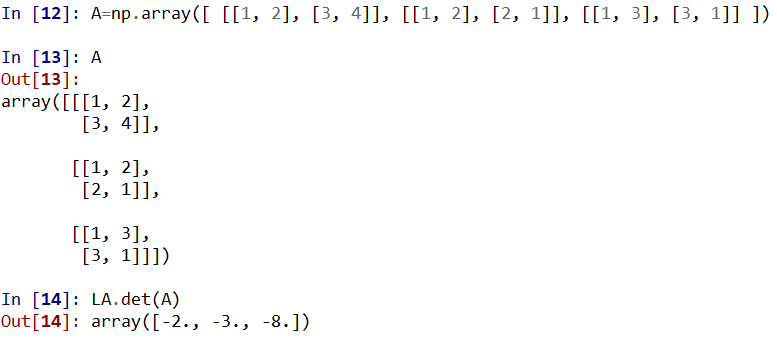
3.2求方阵的特征值、特征向量：eig

 

 

3.3求方阵的逆矩阵:：inv

 

 

3.4求解线性方程组：solve

Solve the system of equations 3 * x0 + x1 = 9 and x0 + 2 * x1 = 8:

 

 

3.5一个方阵的整数次幂：matrix_power

 

 

 

3.6计算在一个函数调用两个或两个以上的阵列的点积：multi_dot

 

4.官网文档

https://docs.scipy.org/doc/numpy/reference/routines.linalg.html