斐波那契数列-矩阵乘法

先简单介绍一下矩阵乘法求斐波那契数列的原理

f(n) 是第n项的值。

f(1)= 1; f(2) =1;

f(n)= f(n-1) + （n-2)

下面的介绍是我从网上查到了，收益匪浅。

分两步推导：

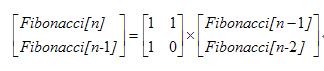
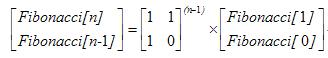
  问题的求解就变成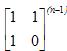的解决，而幂的求可用二分法来求。

二分法可用递归和非递归来求：

下面是代码：

定义矩阵

struct matrix                  //定义2*2的矩阵 

{

    int a[2][2];

};

void mul(matrix& x,matrix& y)  // 矩阵乘法 x = x*y

{

matrix ans;

ans.a[0][0]=x.a[0][0]*y.a[0][0]+x.a[0][1]*y.a[1][0];

ans.a[0][1]=x.a[0][0]*y.a[0][1]+x.a[0][1]*y.a[1][1];

ans.a[1][0]=x.a[1][0]*y.a[0][0]+x.a[1][1]*y.a[1][0];

ans.a[1][1]=x.a[1][0]*y.a[0][1]+x.a[1][1]*y.a[1][1];

x = ans;

}

//下面这个函数是我从网上查到的 

matrix power(matrix x,long e)

{

matrix ans,tmp;

if(e==0)                    //指数为0的时候,返回单位矩阵

{

ans.a[0][0]=1;

ans.a[0][1]=0;

ans.a[1][0]=0;

ans.a[1][1]=1;

return ans;

}

if( e==1 )

return x;

tmp=power(x,e>>1);     //X的e/2次方 

ans=mul(tmp,tmp);

if( e&1 )                  //如果e为奇数,还要再乘以X 

ans=mul(ans,x);

return ans;

}

非递归代码：

matrix result = {{1,0,0,1}};

matrix base ={{1,1,1,0}};

if(n&1) result = base;

n>>=1;

while(n)

{

mul2(base, base);

if(n&1)

{

    mul2(result, base);

}

n>>=1;

}

<<result.a[0][1]就是第 n项 的值。