快速幂运算
在计算 xn 时,我们会怎么算呢?如果只是x * x * x * ... * x 这样每个数乘起来计算 n 次的的话,虽然算法简单,但是复杂度为 O(n) ,往往不能满足要求。让我们来考虑加速幂运算的方法。
思路一:
如果 n = 2k ,可以将其表示为 xn = ((x2)2)... ,只要做 k 次平方运算就可以轻松求得。由此我们想到,先将 n 表示为2的幂次的和 n = 2k1 + 2k2 + 2k3 + ... ,就有 xn = x2^k1 x2^k2 x2^k3 ... ,只要在依次求 x2^i 的同时计算就好了,最终得到了 O(logn) 计算幂运算的算法。比如计算x22,可以把 x22 表示为 x2 * x4 * x16 (22转成二进制是10110)。在进行幂运算时,往往因为结果数字过大,而让我们输出取余后的结果。下面给出代码:
typedef long long ll;
ll mod_pow(ll x,ll n,ll mod){
ll res = 1;
while(n>0){
if(n&1) res = res * x % mod;
//如果二进制最低位为1,则乘上x^(2^i)
x = x * x % mod; //将x平方
n >>= 1;
}
return res;
}
思路二:
当n为偶数时有 xn = ((x2)(n/2)) ,递归转为n/2的情况;n为奇数时有 xn = ((x2)(n/2)) * x ,同样也递归转为 n/2 的情况。这样不断递归下去,每次n都减半,于是可以在O(logn)时间内完成幂运算。这个比第一种似乎更容易想到也更易理解,下面给出代码:
typedef long long ll;
ll mod_pow(ll x,ll n,ll mod){
if(n == 0) return 1;
if(n == 1) return x % mod;
ll res = mod_pow(x * x % mod, n / 2, mod);
if(n & 1)
res = res * x % mod;
return res;
}
思路三:
还有一种非常类似的,f(x,n) = xn,x为奇数那么f(x,n) = f(x,n/2) * f(x,n/2) *x,x为偶数那么f(x,n) = f(x,n/2) * f(x,n/2)。
ll f(int x,int n){
if(n==0) return 1;
if(n==1) return x;
if(n&1) return f(x,n>>1)*f(x,n>>1)*x; //如果n是奇数
else return f(x,n>>1)*f(x,n>>1); //如果n是偶数
}
快速乘法
适用范围:快速计算a*b % mod的结果(主要目的是换乘法为加法,防止爆数据),或者快速计算a^b % mod 的结果,时间复杂度大大降低。
算法描述:首先你可能会问a*b不是直接乘就出来了么,为什么需要快速算法?但是乘法在计算机中处理的时间并不是这么快的,也要拆分为加法来做的。所以快速乘法会更快的计算a*b的结果,而且a*b%mod可能还没取模就已经爆long long,但快速乘法却不会。快速幂也是同样的道理。
实现的原理都是基于按照二进制位一步一步乘来避免重复的操作,利用前面的中间结果,从而实现快速的目的。
对于乘数b来说,势必可以拆成2进制,比如110101。有一些位为0,有一些位为1。根据乘法分配律:a*b=a*(b1+b2+b3+……)
那么对于a*53 = a*110101(二进制)= a*(100000+10000+100+1)=a*(100000*1+10000*1+1000*0+100*1+10*0+1*1)。
那么设立一个ans=0用于保存答案,每一位让a*=2,在根据b的对应为1看是不是加上此时的a,即可完成快速运算。比如刚才的例子让a=5,运转流程如下。
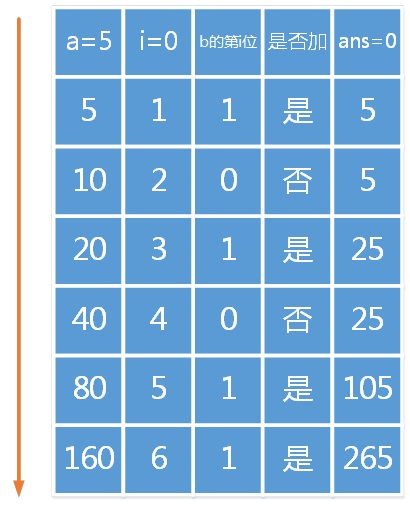
即可计算出5*53=265。
不知道看到这里你发现了没有,其实对于快速幂其实是一样的道理,只不过每一位a更新的时候不是*2,而是a=a*a,ans+变成ans*。
例如3^9的流程如下:3^5=3^(1001) (二进制)= 3^(1000*1+100*0+10*0+1*1)
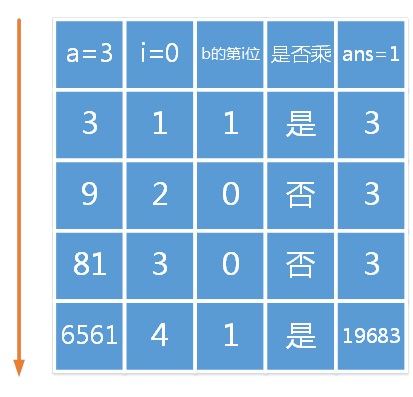
最后说一些细节吧,如果要取模在ans+、ans*、和a更新的时候都%mod即可。然后b一位一位的读取每次b/=2或者b>>=1,表示b向右移动一位,再与1做&操作即可。(见代码)
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
using namespace std;
long long q_mul(long long a,long long b,long long mod)
// 快速计算 (a*b) % mod
{
long long ans=0;
while(b)
{
if(b&1) //如果当前位为1
{
b--;
ans =(ans+a)%mod; //ans+=a
}
b>>=1;
a=(a+a)%mod;
}
return ans;
}
long long q_pow(long long a,long long b,long long mod)
//快速计算 (a^b) % mod
{
long long ans=1;
while(b)
{
if(b&1)
ans=q_mul(ans,a,mod); //ans*=a
b>>=1;
a=q_mul(a,a,mod);
}
return ans;
}
int main( )
{
long long a, b, n;
while(cin >> a >> b >> n)
{
cout << "a*b%n = " << q_mul( a, b, n ) << endl;
cout << "a^b%n = " << q_pow( a, b, n ) << endl;
}
return 0;
}
// 本文部分参考:https://blog.csdn.net/maxichu/article/details/45459715