HDU 1710 Binary Tree Traversals

Binary Tree Traversals

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.

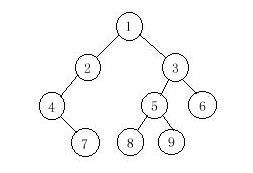
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.

In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.

In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.

Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

 

Input

The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.

 

Output

For each test case print a single line specifying the corresponding postorder sequence.

 

Sample Input

9
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6

 

Sample Output

7 4 2 8 9 5 6 3 1

和小白里面的那题差不多，参考小白完成。

真心佩服lrj，如此巧妙的代码让我受益匪浅啊。。。

AC代码：

#include <cstdio>
#define MAX 1001

void build(int n, int *s1, int *s2, int *s)
{
    if(n <= 0)
        return;
    int p;
    for(int i=0; i < n; i++)
        if(s1[0] == s2[i])
		{
            p = i;
			break;
		}
    build(p, s1 + 1, s2, s);
    build(n - p - 1, s1 + p + 1, s2 + p + 1, s + p);
    s[n - 1] = s1[0];
}

int main()
{
    int s1[MAX],s2[MAX],ans[MAX];
    int n;
    while (scanf("%d", &n) != EOF)
    {
        for(int i=0; i<n; i++)
            scanf("%d", &s1[i]);
        for(int i=0; i<n; i++)
            scanf("%d", &s2[i]);
        build(n, s1, s2, ans);
        for(int i = 0; i < n - 1; i++)
            printf("%d ", ans[i]);
        printf("%d\n", ans[n - 1]);
    }
    return 0;
}