首先来看看数据结构和算法解决的是什么问题? 他解决的是 让代码运行更快以及如何让代码更省内存
那怎么去看你的程序是否快以及省内存呢? 这里有两个概念 时间复杂度以及空间复杂度
我们一般使用大O复杂度表示法来表示程序的运行速度
(当然可能有同学会说,我直接把代码跑一遍,在开始,结束的时候记录时间,不也可以计算出来吗?
可以倒是可以,但是有很大的局限性,比如不同的机器跑出来的结果是不一样的,所以一般不使用)
算法的执行速度初略的讲,就是代码的运行时间 那我们如何能够简略的得到一段代码的运行时间呢
下面举个例子
比如下面有一个求1-n的和的代码
int sum = 0;
int i = 1;
for (; i <= n; ++i)
{
sum=sum+ i;
}
我们假设 每行代码的执行时间都一样(因为我们这里是简单的循环哈) 这里假设为X
那么我们知道 这个循环一共需要执行 定义两个变量2次,整个循环会执行2n次 一共花费时间(2n+2)*X,可以看出执行时间的长短和n成正比
因此,我们可以看到一个很简单的现象,就是 程序运行的总的时间和每行代码的执行次数成正比
于是乎,经典的大O表示法来了
T(n) = O(f(n))
其中,T(n) 它表示代码执行的时间;n 表示数据规模的大小;f(n) 表示每行代码执行的次数总和。因为这是一个公式,所以用 f(n) 来表示。公式中的 O,表示代码的执行时间 T(n) 与 f(n) 表达式成正比
比如我们求和代码 可以表示为T(n) = O(2n+2)
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度,简称时间复杂度。
那我们如何去分析一段程序的时间复杂度呢?
一般来说有以下常用的三个方法
1、仅仅关注执行次数最多的代码
因为大O表示法只是表示一种趋势,所以我们可以忽略次要的,仅仅的关注执行次数最多的代码(也就是循环,递归等代码)
还是用求和的例子来说明
int sum = 0;
int i = 1;
for (; i <= n; ++i)
{
sum=sum+ i;
}
其中第一行和第二行都是常量级别的执行时间,和n无关,对咋们的执行时间影响最多的是循环中的代码,这两行代码一共执行了2n次 ,所以总的时间复杂度就是 O(2n),但是我们用大O表示的时候一般会省略n前面的常数项,所以最后表示为O(n)
2、乘法规则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
如果 T1(n)=O(f(n)),T2(n)=O(g(n));
那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n)).
落实到具体的代码,我们可以简单的把乘法规则看成是嵌套循环
比如
int sum(int n) {
int sum = 0;
int i = 1;
for (; i <= n; ++i) {
sum = sum + i;
for (int j = 1; j < n; j++)
{
sum = sum + j;
}
}
return sum;
}
我们可以看到 sum中有一个嵌套循环,外层会执行n次,内层 的话,外层没执行一次,内层就会执行n次,所以总的次数是n*n 也就是O(n^2)
3、最大法则:总的复杂度等于所有复杂度中量级最大的那段代码的复杂度
请看下列代码
int sum(int n) {
int sum = 0;
for (int i = 1; i < 10000; i++) {
sum = sum + i;
}
for (int i = 1; i <= n; i++) {
sum = sum + i;
}
for (int i = 1; i <= n; ++i) {
sum = sum + i;
for (int j = 1; j < n; j++) {
sum = sum + j;
}
}
return sum;
}
一共有三个循环相对执行次数多点,我们来依次分析
第一循环的时间复杂度是多少呢?这段代码循环执行了 10000 次,所以是一个常量的执行时间,跟 n 的规模无关。
(因为我们的大O表示法关注的是一个趋势,所以当n无限大的时候,常数是可以忽略的)
那第二个循环和第三个循环的时间复杂度分别是多少呢?答案是 O(n) 和 O(n^2),比较简单,就不分析了
所以他的复杂度应该是n^2 +n 但是根据我们的最大原则,所以最后的复杂度是O(n^2)
抽象成公式就是:如果 T1(n)=O(f(n)),T2(n)=O(g(n));
那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n)))=O(max(f(n), g(n)))
常见的复杂度分析
虽然代码千差万别,但是下面的这些复杂度量级几乎涵盖了你今后可以接触的所有代码的复杂度量级。
常数阶O(1)
对数阶O(logN)
线性阶O(n)
线性对数阶O(nlogN)
平方阶O(n²)
立方阶O(n³)
指数阶(2^n)
阶乘阶 n!
下面来看看常见的时间复杂度代码
1、O(1)
O(1) 只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。
比如下面的这段代码,
即便有 3 行,
int i = 1;
int j = 2;
int max= i > j ? i : j;
它的时间复杂度也是 O(1),而不是 O(3)。
只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度我们都记作 O(1)。
或者说,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
2、O(logn)、O(nlogn)
看下面的代码的 复杂度是多少?
int i=1;
while (i <= n) {
i = i * 2;
}
老办法,我们还是看代码执行多少次吧
首先根据代码
代码从1 ->2->4->8->16一直到n
其实是一个等比数列
也就是2^0 ->2^1->2^2->2^3->2^4 一直到n
其实代码的意思就是想知道2的多少次方等于n
也就是2^x = n 我们要求x ,直接取对数, x=log2n,所以,这段代码的时间复杂度就是 O(log2n)
如果你理解了O(logn),那 O(nlogn) 就很容易理解了。根据乘法规则:
如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,时间复杂度就是 O(nlogn) 了。
而且,O(nlogn) 也是一种非常常见的算法时间复杂度。比如,归并排序、快速排序,堆排序的时间复杂度都是 O(nlogn)
3、O(m+n)
int sum(int m, int n) {
int sum1 = 0;
int sum2 = 0;
for (int i = 1; i <= m; i++) {
sum1 = sum1 + i;
}
for (int i = 1; i <= n; i++) {
sum2 = sum2 + i;
}
return sum1 + sum2;
}
从代码中可以看出,m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大,所以我们在表示复杂度的时候,就不能简单地利用最大法则,省略掉其中一个。所以,上面代码的时间复杂度就是 O(m+n)
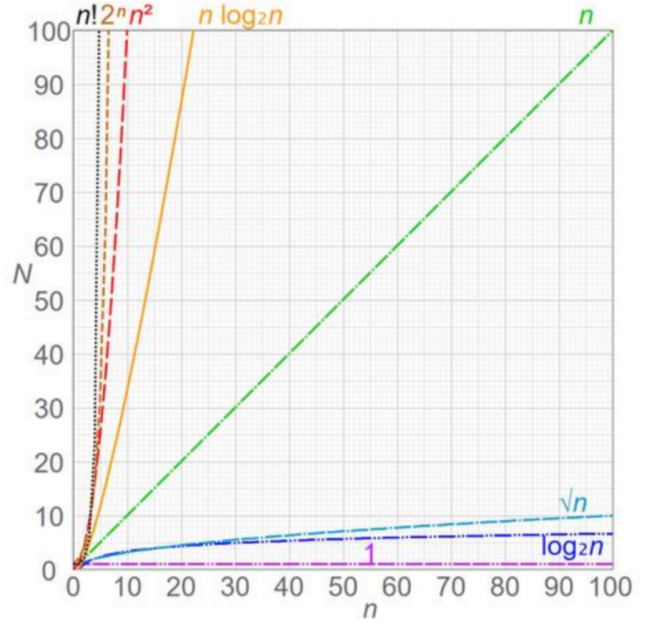
最后用一个图来比较下常见的时间复杂度的差异(趋势)吧
空间复杂度
我们知道时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。
类比一下,空间复杂度全称就是渐进空间复杂度,表示算法的内存与数据规模之间的增长关系。依然使用大O表示法
直接上代码
int i = 0;
int[] a = new int[n];
可以看到,int i = 0,表示一个常量阶的空间消耗,和n无关,我们可以忽略
int[] a = new int[n]; 申请了一个大小为 n 的 int 类型数组,所以整段代码的空间复杂度就是 O(n)
我们常见的空间复杂度就是 O(1)、O(n)、O(n2 ),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。可以直接不用管
可以看到,空间复杂度分析比时间复杂度分析要简单很多。就看需要申请多少内存就可以知道
最后
希望以后大家在写完代码以后,可以自行分析下代码的时间和空间复杂度,看能否进一步优化自己的代码。
(毕竟,优秀的工程师,都会在意自己的代码性能)