二叉搜索树（BST）

二叉搜索树需满足以下四个条件：

 1.若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

 2.若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

 3.任意节点的左、右子树也分别为二叉查找树；

 4.没有键值相等的节点。

 如下图所示：

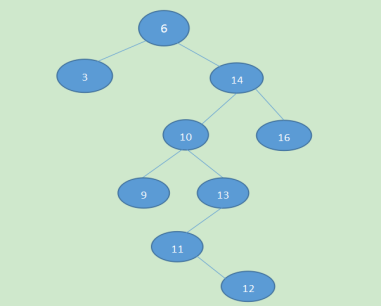
这里主要分析下删除操作，（插入操作比较简单，这里暂不分析）

删除操作主要有以下几种情况

 1.要删除的节点是一个叶子节点,直接使用她的父节点删除即可。

 2.要删除的节点是只有左孩子节点，直接用当前要删除的节点的左孩子替换要删除的节点。

 3.要删除的节点是只有右孩子节点，直接用当前要删除的节点的右孩子替换要删除的节点。

 4.要删除的节点是既有左孩子，又有右孩子，

 首先我们需要找到哪个值来覆盖当前要删除的节点，很明显，就是刚刚把她大的那个数。也就是她的直接中序后继节点，也就是当前节点的右子树中 值最小的节点，并且此中序后继节点一定不含子节点或者只含有一个右孩子 

找到该节点以后把值赋给当前要删除的节点即可。并删除该直接中序后继节点 （如果没有子节点的话），如果有子节点 需要把他的右子节点移动到他的位置。

下面是源代码

class Node {
	int data;
	Node leftChild;
	Node rightChild;

	public Node(int key) {
		this.data = key;
	}
}

public class BST {
	Node root;

	public void insert(int data) {
		if (root == null) {
			root = new Node(data);
			return;
		}
		Node currentNode = root;
		Node parentNode = root;
		boolean isLeftChild = true;
		while (currentNode != null) {
			parentNode = currentNode;
			if (data < currentNode.data) {
				currentNode = currentNode.leftChild;
				isLeftChild = true;
			} else {
				currentNode = currentNode.rightChild;
				isLeftChild = false;
			}
		}
		Node newNode = new Node(data);
		if (isLeftChild) {
			parentNode.leftChild = newNode;
		} else {
			parentNode.rightChild = newNode;
		}
	}

	public boolean delete(int data) {
		// 首先先找到该节点
		Node currentParentNode = root;
		Node currentNode = root;
		boolean isLeftChild = false; // 用来记录当前查找的节点是他父节点的左孩子还是右孩子
		while (currentNode != null && currentNode.data != data) {
			currentParentNode = currentNode;
			if (data < currentNode.data) {
				currentNode = currentNode.leftChild;
				isLeftChild = true;
			} else {
				currentNode = currentNode.rightChild;
				isLeftChild = false;
			}

		}
		if (currentNode == null) {
			return false;
		}
		// System.out.println("p " + currentParentNode.data);
		// System.out.println("c " + currentNode.data + "isLeft " + isLeftChild);
		// 找到了该节点
		if (currentNode.leftChild == null && currentNode.rightChild == null) {
			if (isLeftChild) {
				currentParentNode.leftChild = null;
			} else {
				currentParentNode.rightChild = null;
			}
		} else if (currentNode.leftChild != null && currentNode.rightChild == null) {
			if (currentNode == root) {
				root = currentNode;
			} else if (isLeftChild) {
				currentParentNode.leftChild = currentNode.leftChild;
			} else {
				currentParentNode.rightChild = currentNode.leftChild;
			}
		} else if (currentNode.leftChild == null && currentNode.rightChild != null) {
			if (currentNode == root) {
				root = currentNode;
			} else if (isLeftChild) {
				currentParentNode.leftChild = currentNode.rightChild;
			} else {
				currentParentNode.rightChild = currentNode.rightChild;
			}
		} else if (currentNode.leftChild != null && currentNode.rightChild != null) {

			// 先找到当前节点的直接中序后继节点
			Node directPostNode = getDirectPostNode2(currentNode);
			currentNode.data = directPostNode.data;
		}
		return true;
	}

	private Node getDirectPostNode2(Node delNode) {
		Node parentNode = delNode;// 用来保存待删除节点的直接后继节点的父亲节点
		Node direcrPostNode = delNode;// 用来保存待删除节点的直接后继节点
		Node temp = delNode.rightChild;
		while (temp != null) {
			parentNode = direcrPostNode;
			direcrPostNode = temp;
			temp = temp.leftChild;
		}
		// 删除该直接后继节点
		if (direcrPostNode != parentNode.rightChild) {
			parentNode.leftChild = direcrPostNode.rightChild;
			direcrPostNode.rightChild = null;
		} else {
			parentNode.rightChild = null;
		}
		return direcrPostNode;
	}

	public void inOrder(Node rootNode) {
		if (rootNode != null) {
			inOrder(rootNode.leftChild);
			System.out.print(" " + rootNode.data);
			inOrder(rootNode.rightChild);
		}
	}

	public static void main(String[] args) {
		BST tree = new BST();
		tree.insert(6);// 插入操作,构造图一所示的二叉树
		tree.insert(3);
		tree.insert(1);
		tree.insert(14);
		tree.insert(16);
		tree.insert(10);
		tree.insert(9);
		tree.insert(13);
		tree.insert(11);
		tree.insert(12);

		tree.inOrder(tree.root);
		System.out.println();
		tree.delete(10);
		tree.inOrder(tree.root);
	}
}

　　

总结：

  BST效率 :       查找最好时间复杂度O(logN)，最坏时间复杂度O(N)（BST退化成单支树结构）。

                            插入删除操作算法简单，时间复杂度与查找差不多

 

另外关于avl(平衡查找树)以rbt以及B-,b+tree
红黑树并不追求“完全平衡”——它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。
红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。当然，还有一些更好的，但实现起来更复杂的数据结构，能够做到一步旋转之内达到平衡。但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同，但统计性能比AVL树更高。大量数据实践证明，RBT的总体统计性能要好于平衡二叉树。AVL树更平衡一些，适合查找多的应用，红黑树插入删除更快一些

B-,b+tree 树大多用于数据库中，可以有效地降低磁盘读取次数