===============================================================================
KAZE算法资源:
1. 论文: http://www.robesafe.com/personal/pablo.alcantarilla/papers/Alcantarilla12eccv.pdf
2. 项目主页:http://www.robesafe.com/personal/pablo.alcantarilla/kaze.html
3. 作者代码:http://www.robesafe.com/personal/pablo.alcantarilla/code/kaze_features_1_4.tar
(需要boost库,另外其计时函数的使用比较复杂,可以用OpenCV的cv::getTickCount代替)
4. Computer Vision Talks的评测:http://computer-vision-talks.com/2013/03/porting-kaze-features-to-opencv/
5. Computer Vision Talks 博主Ievgen Khvedchenia将KAZE集成到OpenCV的cv::Feature2D类,但需要重新编译OpenCV,并且没有实现算法参数调整和按Mask过滤特征点的功能:https://github.com/BloodAxe/opencv/tree/kaze-features
6. 我在Ievgen的项目库中提取出KAZE,封装成继承cv::Feature2D的类,无需重新编译OpenCV,实现了参数调整和Mask过滤的功能: https://github.com/yuhuazou/kaze_opencv
7. Matlab 版的接口程序,封装了1.0版的KAZE代码:https://github.com/vlfeat/vlbenchmarks/blob/unstable/%2BlocalFeatures/Kaze.m
===============================================================================
2.2.2 特征点检测
KAZE的特征点检测与SIFT类似,是通过寻找不同尺度归一化后的Hessian局部极大值点来实现的。Hessian矩阵的计算如下:
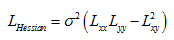
其中σ是尺度参数σi的整数值。在寻找极值点时,每一个像素点和它所有的相邻点比较,当其大于它的图像域和尺度域的所有相邻点时,即为极值点。理论上其比较的范围是当前尺度、上一尺度和下一尺度上的3个大小为σi×σi的矩形窗口。不过为了加快搜索速度,窗口大小固定为3×3,则搜索空间是一个边长为3像素的立方体:中间的检测点和它同尺度的8个相邻点,以及和上下相邻尺度对应的9×2个点——共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。

KAZE 特征点的类定义如下:
// Ipoint Class Declaration
class Ipoint
{
public:
// 特征点的浮点坐标和整数坐标(Coordinates of the detected interest point)
float xf,yf; // Float coordinates
int x,y; // Integer coordinates
// 特征点的尺度级别,σ为单位(Detected scale of the interest point (sigma units))
float scale;
// 图像尺度参数的整数值(Size of the image derivatives (pixel units))
int sigma_size;
// 特征检测响应值(Feature detector response)
float dresponse;
// 进化时间(Evolution time)
float tevolution;
// 特征点所属的Octave组(Octave of the keypoint)
float octave;
// 特征点所属的层级(Sublevel in each octave of the keypoint)
float sublevel;
// 特征点的描述向量(Descriptor vector and size)
std::vector<float> descriptor;
int descriptor_size;
// 特征点的主方向(Main orientation)
float angle;
// 描述向量类型(Descriptor mode)
int descriptor_mode;
// 拉普拉斯标志值(Sign of the laplacian (for faster matching))
int laplacian;
// 进化级别(Evolution Level)
unsigned int level;
// Constructor
Ipoint(void);
};
可见KAZE特征点Ipoint的结构与OpenCV的KeyPoint类相比多了很多参数,为了方便在OpenCV中调用,需要构造Ipoint与KeyPoint的转换函数。具体如下:
/***
* Convertions between cv::Keypoint and KAZE::Ipoint
*/
static inline void convertPoint(const cv::KeyPoint& kp, Ipoint& aux)
{
aux.xf = kp.pt.x;
aux.yf = kp.pt.y;
aux.x = fRound(aux.xf);
aux.y = fRound(aux.yf);
//cout << "SURF size: " << kpts_surf1_[i].size*.5 << endl;
aux.octave = kp.octave;
// Get the radius for visualization
aux.scale = kp.size*.5/2.5;
aux.angle = DEGREE_TO_RADIAN(kp.angle);
//aux.descriptor_size = 64;
}
static inline void convertPoint(const Ipoint& src, cv::KeyPoint& kp)
{
kp.pt.x = src.xf;
kp.pt.y = src.yf;
kp.angle = RADIAN_TO_DEGREE(src.angle);
kp.response = src.dresponse;
kp.octave = src.octave;
kp.size = src.scale;
}
值得注意的是,KAZE特征点的描述向量需要用到 Ipoint 的一个关键参数 level ,即特征点在非线性尺度空间中所处的进化级别。这个参数是 OpenCV 其它特征检测算法没有的。因此,KAZE 特征点可以使用其它特征描述算法来表征,但其它特征检测算法生成的关键点却无法用 KAZE 描述向量来表征。
在具体计算时,首先生成每个像素点在各个层级的检测响应,获得像素点的Hessian行列式值,然后再寻找局部极大值。具体代码如下:
//*************************************************************************************
//*************************************************************************************
/**
* @brief This method selects interesting keypoints through the nonlinear scale space
*/
void KAZE::Feature_Detection(std::vector<Ipoint> &kpts)
{
if( verbosity == true )
{
std::cout << "\n> Detecting features. " << std::endl;
}
int64 t1 = cv::getTickCount();
// Firstly compute the detector response for each pixel and scale level
Compute_Detector_Response();
// Find scale space extrema
Determinant_Hessian_Parallel(kpts);
// Perform some subpixel refinement
if( SUBPIXEL_REFINEMENT == true )
{
Do_Subpixel_Refinement(kpts);
}
int64 t2 = cv::getTickCount();
tdetector = 1000.0*(t2-t1) / cv::getTickFrequency();
if( verbosity == true )
{
std::cout << "> Feature detection done. Execution time (ms): " << tdetector << std::endl;
}
}
//*************************************************************************************
//*************************************************************************************
/**
* @brief This method computes the feature detector response for the nonlinear scale space
* @note We use the Hessian determinant as feature detector
*/
void KAZE::Compute_Detector_Response(void)
{
float lxx = 0.0, lxy = 0.0, lyy = 0.0;
float *ptr;
int64 t1 = cv::getTickCount();
// Firstly compute the multiscale derivatives
Compute_Multiscale_Derivatives();
for( unsigned int i = 0; i < evolution.size(); i++ )
{
// Determinant of the Hessian
if( verbosity == true )
{
std::cout << "--> Computing Hessian determinant. Evolution time: " << evolution[i].etime << std::endl;
}
for( int ix = 0; ix < img_height; ix++ )
{
for( int jx = 0; jx < img_width; jx++ )
{
// Get values of lxx,lxy,and lyy
ptr = evolution[i].Lxx.ptr<float>(ix);
lxx = ptr[jx];
ptr = evolution[i].Lxy.ptr<float>(ix);
lxy = ptr[jx];
ptr = evolution[i].Lyy.ptr<float>(ix);
lyy = ptr[jx];
// Compute ldet
ptr = evolution[i].Ldet.ptr<float>(ix);
ptr[jx] = (lxx*lyy-lxy*lxy);
}
}
}
int64 t2 = cv::getTickCount();
tdresponse = 1000.0 * (t2-t1) / cv::getTickFrequency();
if( verbosity == true )
{
std::cout << "-> Computed detector response. Execution time (ms): " << tdresponse << std::endl;
}
}
//*************************************************************************************
//*************************************************************************************
/**
* @brief This method performs the detection of keypoints by using the normalized
* score of the Hessian determinant through the nonlinear scale space
* @note We compute features for each of the nonlinear scale space level in a different processing thread
*/
void KAZE::Determinant_Hessian_Parallel(std::vector<Ipoint> &kpts)
{
int64 t1 = cv::getTickCount();
unsigned int level = 0;
float dist = 0.0, smax = 3.0;
int npoints = 0, id_repeated = 0;
int left_x = 0, right_x = 0, up_y = 0, down_y = 0;
bool is_extremum = false, is_repeated = false, is_out = false;
// Delete the memory of the vector of keypoints vectors
// In case we use the same kaze object for multiple images
for( unsigned int i = 0; i < kpts_par.size(); i++ )
{
vector<Ipoint>().swap(kpts_par[i]);
}
kpts_par.clear();
vector<Ipoint> aux;
// Create multi-thread
//boost::thread_group mthreads;
// Allocate memory for the vector of vectors
for( unsigned int i = 1; i < evolution.size()-1; i++ )
{
kpts_par.push_back(aux);
}
// Find extremum at each scale level
for( unsigned int i = 1; i < evolution.size()-1; i++ )
{
if( verbosity == true )
{
std::cout << "--> Finding scale space extrema. Evolution time: " << evolution[i].etime << std::endl;
}
// Create the thread for finding extremum at i scale level
//mthreads.create_thread(boost::bind(&KAZE::Find_Extremum_Threading,this,i));
Find_Extremum_Threading(i);
}
// Wait for the threads
//mthreads.join_all();
// Now fill the vector of keypoints!!!
if( verbosity == true )
{
std::cout << "--> Fill the vector of keypoints. " << std::endl;
}
for( unsigned int i = 0; i < kpts_par.size(); i++ )
{
for( unsigned int j = 0; j < kpts_par[i].size(); j++ )
{
level = i+1;
is_extremum = true;
is_repeated = false;
is_out = false;
// Check in case we have the same point as maxima in previous evolution levels (ONLY work when kpts is not empty)
for( unsigned int ik = 0; ik < kpts.size(); ik++ )
{
if( kpts[ik].level == level || kpts[ik].level == level+1 || kpts[ik].level == level-1 )
{
dist = pow(kpts_par[i][j].xf-kpts[ik].xf,2)+pow(kpts_par[i][j].yf-kpts[ik].yf,2);
if( dist < evolution[level].sigma_size*evolution[level].sigma_size )
{
if( kpts_par[i][j].dresponse > kpts[ik].dresponse )
{
id_repeated = ik;
is_repeated = true;
}
else
{
is_extremum = false;
}
break;
}
}
}
if( is_extremum == true )
{
// Check that the point is under the image limits for the descriptor computation
left_x = fRound(kpts_par[i][j].xf-smax*kpts_par[i][j].scale);
right_x = fRound(kpts_par[i][j].xf+smax*kpts_par[i][j].scale);
up_y = fRound(kpts_par[i][j].yf-smax*kpts_par[i][j].scale);
down_y = fRound(kpts_par[i][j].yf+smax*kpts_par[i][j].scale);
if( left_x < 0 || right_x > evolution[level].Ldet.cols || up_y < 0 || down_y > evolution[level].Ldet.rows)
{
is_out = true;
}
if( is_out == false )
{
if( is_repeated == false )
{
kpts.push_back(kpts_par[i][j]);
npoints++;
}
else
{
kpts[id_repeated] = kpts_par[i][j];
}
}
}
}
}
int64 t2 = cv::getTickCount();
double thessian = 1000.0 * (t2-t1) / cv::getTickFrequency();
if( verbosity == true )
{
std::cout << "-> Computed Hessian determinant. Execution time (ms):" << thessian << std::endl;
}
}
//*************************************************************************************
//*************************************************************************************
/**
* @brief This method is called by the thread which is responsible of finding extrema
* at a given nonlinear scale level
* @param level Index in the nonlinear scale space evolution
*/
void KAZE::Find_Extremum_Threading(int level)
{
float value = 0.0;
bool is_extremum = false;
for( int ix = 1; ix < img_height-1; ix++ )
{
for( int jx = 1; jx < img_width-1; jx++ )
{
is_extremum = false;
value = *(evolution[level].Ldet.ptr<float>(ix)+jx);
// Filter the points with the detector threshold
if( value > dthreshold && value >= DEFAULT_MIN_DETECTOR_THRESHOLD )
{
if( value >= *(evolution[level].Ldet.ptr<float>(ix)+jx-1) )
{
// First check on the same scale
if( Check_Maximum_Neighbourhood(evolution[level].Ldet,1,value,ix,jx,1))
{
// Now check on the lower scale
if( Check_Maximum_Neighbourhood(evolution[level-1].Ldet,1,value,ix,jx,0) )
{
// Now check on the upper scale
if( Check_Maximum_Neighbourhood(evolution[level+1].Ldet,1,value,ix,jx,0) )
{
is_extremum = true;
}
}
}
}
}
// Add the point of interest!!
if( is_extremum == true )
{
Ipoint point;
point.xf = jx; point.yf = ix;
point.x = jx; point.y = ix;
point.dresponse = fabs(value);
point.scale = evolution[level].esigma;
point.sigma_size = evolution[level].sigma_size;
point.tevolution = evolution[level].etime;
point.octave = evolution[level].octave;
point.sublevel = evolution[level].sublevel;
point.level = level;
point.descriptor_mode = descriptor_mode;
point.angle = 0.0;
// Set the sign of the laplacian
if( (*(evolution[level].Lxx.ptr<float>(ix)+jx) + *(evolution[level].Lyy.ptr<float>(ix)+jx)) > 0 )
{
point.laplacian = 0;
}
else
{
point.laplacian = 1;
}
kpts_par[level-1].push_back(point);
}
}
}
}
在找到特征点的位置后,再进行亚像素的精确定位,采用的是Lowe在BMVC2002提出的方法[6]。即根据Taylor展开式:
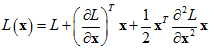
特征点的亚像素坐标的解为:
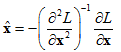
具体的实现代码如下:
//*************************************************************************************
//*************************************************************************************
/**
* @brief This method performs subpixel refinement of the detected keypoints
*/
void KAZE::Do_Subpixel_Refinement(std::vector<Ipoint> &keypts)
{
float Dx = 0.0, Dy = 0.0, Ds = 0.0, dsc = 0.0;
float Dxx = 0.0, Dyy = 0.0, Dss = 0.0, Dxy = 0.0, Dxs = 0.0, Dys = 0.0;
int x = 0, y = 0, step = 1;
cv::Mat A = cv::Mat::zeros(3,3,CV_32F);
cv::Mat b = cv::Mat::zeros(3,1,CV_32F);
cv::Mat dst = cv::Mat::zeros(3,1,CV_32F);
int64 t1 = cv::getTickCount();
for( unsigned int i = 0; i < keypts.size(); i++ )
{
x = keypts[i].x;
y = keypts[i].y;
// Compute the gradient
Dx = (1.0/(2.0*step))*(*(evolution[keypts[i].level].Ldet.ptr<float>(y)+x+step)
-*(evolution[keypts[i].level].Ldet.ptr<float>(y)+x-step));
Dy = (1.0/(2.0*step))*(*(evolution[keypts[i].level].Ldet.ptr<float>(y+step)+x)
-*(evolution[keypts[i].level].Ldet.ptr<float>(y-step)+x));
Ds = 0.5*(*(evolution[keypts[i].level+1].Ldet.ptr<float>(y)+x)
-*(evolution[keypts[i].level-1].Ldet.ptr<float>(y)+x));
// Compute the Hessian
Dxx = (1.0/(step*step))*(*(evolution[keypts[i].level].Ldet.ptr<float>(y)+x+step)
+ *(evolution[keypts[i].level].Ldet.ptr<float>(y)+x-step)
-2.0*(*(evolution[keypts[i].level].Ldet.ptr<float>(y)+x)));
Dyy = (1.0/(step*step))*(*(evolution[keypts[i].level].Ldet.ptr<float>(y+step)+x)
+ *(evolution[keypts[i].level].Ldet.ptr<float>(y-step)+x)
-2.0*(*(evolution[keypts[i].level].Ldet.ptr<float>(y)+x)));
Dss = *(evolution[keypts[i].level+1].Ldet.ptr<float>(y)+x)
+ *(evolution[keypts[i].level-1].Ldet.ptr<float>(y)+x)
-2.0*(*(evolution[keypts[i].level].Ldet.ptr<float>(y)+x));
Dxy = (1.0/(4.0*step))*(*(evolution[keypts[i].level].Ldet.ptr<float>(y+step)+x+step)
+(*(evolution[keypts[i].level].Ldet.ptr<float>(y-step)+x-step)))
-(1.0/(4.0*step))*(*(evolution[keypts[i].level].Ldet.ptr<float>(y-step)+x+step)
+(*(evolution[keypts[i].level].Ldet.ptr<float>(y+step)+x-step)));
Dxs = (1.0/(4.0*step))*(*(evolution[keypts[i].level+1].Ldet.ptr<float>(y)+x+step)
+(*(evolution[keypts[i].level-1].Ldet.ptr<float>(y)+x-step)))
-(1.0/(4.0*step))*(*(evolution[keypts[i].level+1].Ldet.ptr<float>(y)+x-step)
+(*(evolution[keypts[i].level-1].Ldet.ptr<float>(y)+x+step)));
Dys = (1.0/(4.0*step))*(*(evolution[keypts[i].level+1].Ldet.ptr<float>(y+step)+x)
+(*(evolution[keypts[i].level-1].Ldet.ptr<float>(y-step)+x)))
-(1.0/(4.0*step))*(*(evolution[keypts[i].level+1].Ldet.ptr<float>(y-step)+x)
+(*(evolution[keypts[i].level-1].Ldet.ptr<float>(y+step)+x)));
// Solve the linear system
*(A.ptr<float>(0)) = Dxx;
*(A.ptr<float>(1)+1) = Dyy;
*(A.ptr<float>(2)+2) = Dss;
*(A.ptr<float>(0)+1) = *(A.ptr<float>(1)) = Dxy;
*(A.ptr<float>(0)+2) = *(A.ptr<float>(2)) = Dxs;
*(A.ptr<float>(1)+2) = *(A.ptr<float>(2)+1) = Dys;
*(b.ptr<float>(0)) = -Dx;
*(b.ptr<float>(1)) = -Dy;
*(b.ptr<float>(2)) = -Ds;
cv::solve(A,b,dst,cv::DECOMP_LU);
if( fabs(*(dst.ptr<float>(0))) <= 1.0
&& fabs(*(dst.ptr<float>(1))) <= 1.0
&& fabs(*(dst.ptr<float>(2))) <= 1.0 )
{
keypts[i].xf += *(dst.ptr<float>(0));
keypts[i].yf += *(dst.ptr<float>(1));
keypts[i].x = fRound(keypts[i].xf);
keypts[i].y = fRound(keypts[i].yf);
dsc = keypts[i].octave + (keypts[i].sublevel+*(dst.ptr<float>(2)))/((float)(DEFAULT_NSUBLEVELS));
keypts[i].scale = soffset*pow((float)2.0,dsc);
}
// Delete the point since its not stable
else
{
keypts.erase(keypts.begin()+i);
i--;
}
}
int64 t2 = cv::getTickCount();
tsubpixel = 1000.0*(t2-t1) / cv::getTickCount();
if( verbosity == true )
{
std::cout << "-> Subpixel refinement done. Execution time (ms): " << tsubpixel << std::endl;
}
}
2.2.3 特征描述向量
(1)特征点主方向
为了实现图像旋转不变性,需要根据特征点的局部图像结构来确定其主方向。这里作者所用的方法与SURF相似,即若特征点的尺度参数为σi,则搜索半径设为6σi。对搜索圈内所有邻点的一阶微分值Lx和Ly通过高斯加权,使得靠近特征点的响应贡献大,而远离特征点的响应贡献小;将这些微分值视作向量空间中的点集,在一个角度为60°的扇形滑动窗口内对点集进行向量叠加,遍历整个圆形区域。获得最长向量的角度就是主方向。
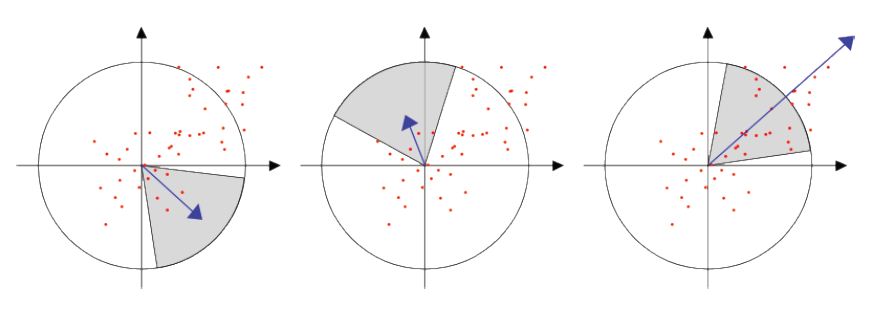
寻找主方向的实现代码如下:
//*************************************************************************************
//*************************************************************************************
/**
* @brief This method computes the main orientation for a given keypoint
* @param kpt Input keypoint
* @note The orientation is computed using a similar approach as described in the
* original SURF method. See Bay et al., Speeded Up Robust Features, ECCV 2006
*/
void KAZE::Compute_Main_Orientation_SURF(Ipoint &kpt)
{
int ix = 0, iy = 0, idx = 0, s = 0;
unsigned int level = kpt.level;
float xf = 0.0, yf = 0.0, gweight = 0.0;
std::vector<float> resX(109), resY(109), Ang(109); // 109 is the maximum grids of size 1 in a circle of radius 6
// Variables for computing the dominant direction
float sumX = 0.0, sumY = 0.0, max = 0.0, ang1 = 0.0, ang2 = 0.0;
// Get the information from the keypoint
xf = kpt.xf;
yf = kpt.yf;
s = kpt.scale;
// Calculate derivatives responses for points within radius of 6*scale
for(int i = -6; i <= 6; ++i)
{
for(int j = -6; j <= 6; ++j)
{
if(i*i + j*j < 36) // the grid is in the circle
{
iy = fRound(yf + j*s);
ix = fRound(xf + i*s);
if( iy >= 0 && iy < img_height && ix >= 0 && ix < img_width )
{
gweight = gaussian(iy-yf,ix-xf,3.5*s);
resX[idx] = gweight*(*(evolution[level].Lx.ptr<float>(iy)+ix));
resY[idx] = gweight*(*(evolution[level].Ly.ptr<float>(iy)+ix));
}
else
{
resX[idx] = 0.0;
resY[idx] = 0.0;
}
Ang[idx] = Get_Angle(resX[idx],resY[idx]);
++idx;
}
}
}
// Loop slides pi/3 window around feature point
for( ang1 = 0; ang1 < M2_PI; ang1+=0.15f)
{
ang2 =(ang1+PI/3.0f > M2_PI ? ang1-5.0f*PI/3.0f : ang1+PI/3.0f);
sumX = sumY = 0.f;
for( unsigned int k = 0; k < Ang.size(); ++k)
{
// Get angle from the x-axis of the sample point
const float & ang = Ang[k];
// Determine whether the point is within the window
if( ang1 < ang2 && ang1 < ang && ang < ang2)
{
sumX+=resX[k];
sumY+=resY[k];
}
else if (ang2 < ang1 &&
((ang > 0 && ang < ang2) || (ang > ang1 && ang < M2_PI) ))
{
sumX+=resX[k];
sumY+=resY[k];
}
}
// if the vector produced from this window is longer than all
// previous vectors then this forms the new dominant direction
if( sumX*sumX + sumY*sumY > max )
{
// store largest orientation
max = sumX*sumX + sumY*sumY;
kpt.angle = Get_Angle(sumX, sumY);
}
}
}
(2)构造特征描述向量
在论文中作者使用M-SURF来描述特征点。对于尺度参数为σi的特征点,在梯度图像上以特征点为中心取一个24σi×24σi的窗口,并将窗口划分为4×4个子区域,每个子区域大小为9σi×9σi,相邻的子区域有宽度为2σi的交叠带。每个子区域都用一个高斯核(σ1 =2.5σi)进行加权,然后计算出长度为4的子区域描述向量:
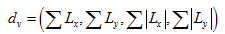
再通过另一个大小为4×4的高斯窗口(σ2 =1.5σi)对每个子区域的向量dv进行加权,最后进行归一化处理。这样就得到了4×4×4=64维的描述向量。
在实现代码中,作者提供了SURF、M-SURF和G-SURF三种描述向量,其中G-SURF是作者在2013年发表的论文[7]中提出的新的特征描述算法。另外,作者还提供了这三种向量的简化计算版本,即将主方向固定为右上方up-right,然后再计算描述向量。默认使用的是64位的M-SURF描述向量,其源码如下:
//*************************************************************************************
//*************************************************************************************
/**
* @brief This method computes the descriptor of the provided keypoint given the
* main orientation of the keypoint
* @param kpt Input keypoint
* @note Rectangular grid of 24 s x 24 s. Descriptor Length 64. The descriptor is inspired
* from Agrawal et al., CenSurE: Center Surround Extremas for Realtime Feature Detection and Matching,
* ECCV 2008
*/
void KAZE::Get_MSURF_Descriptor_64(Ipoint &kpt)
{
float scale = 0.0, dx = 0.0, dy = 0.0, mdx = 0.0, mdy = 0.0, gauss_s1 = 0.0, gauss_s2 = 0.0;
float rx = 0.0, ry = 0.0, rrx = 0.0, rry = 0.0, len = 0.0, xf = 0.0, yf = 0.0, ys = 0.0, xs = 0.0;
float sample_x = 0.0, sample_y = 0.0, co = 0.0, si = 0.0, angle = 0.0;
float fx = 0.0, fy = 0.0, res1 = 0.0, res2 = 0.0, res3 = 0.0, res4 = 0.0;
int x1 = 0, y1 = 0, x2 = 0, y2 = 0, sample_step = 0, pattern_size = 0;
int kx = 0, ky = 0, i = 0, j = 0, dcount = 0;
int dsize = 0, level = 0;
// Subregion centers for the 4x4 gaussian weighting
float cx = -0.5, cy = 0.5;
// Set the descriptor size and the sample and pattern sizes
dsize = kpt.descriptor_size = 64;
sample_step = 5;
pattern_size = 12;
// Get the information from the keypoint
yf = kpt.yf;
xf = kpt.xf;
scale = kpt.scale;
angle = kpt.angle;
level = kpt.level;
co = cos(angle);
si = sin(angle);
// Allocate the memory for the vector
kpt.descriptor = vector<float>(kpt.descriptor_size);
i = -8;
// Calculate descriptor for this interest point
// Area of size 24 s x 24 s
while(i < pattern_size)
{
j = -8;
i = i-4;
cx += 1.0;
cy = -0.5;
while(j < pattern_size)
{
dx=dy=mdx=mdy=0.0;
cy += 1.0;
j = j - 4;
ky = i + sample_step;
kx = j + sample_step;
xs = xf + (-kx*scale*si + ky*scale*co);
ys = yf + (kx*scale*co + ky*scale*si);
for (int k = i; k < i + 9; ++k)
{
for (int l = j; l < j + 9; ++l)
{
// Get coords of sample point on the rotated axis
sample_y = yf + (l*scale*co + k*scale*si);
sample_x = xf + (-l*scale*si + k*scale*co);
// Get the gaussian weighted x and y responses
gauss_s1 = gaussian(xs-sample_x,ys-sample_y,2.5*scale);
y1 = fRound(sample_y-.5);
x1 = fRound(sample_x-.5);
Check_Descriptor_Limits(x1,y1,img_width,img_height);
y2 = fRound(sample_y+.5);
x2 = fRound(sample_x+.5);
Check_Descriptor_Limits(x2,y2,img_width,img_height);
fx = sample_x-x1;
fy = sample_y-y1;
res1 = *(evolution[level].Lx.ptr<float>(y1)+x1);
res2 = *(evolution[level].Lx.ptr<float>(y1)+x2);
res3 = *(evolution[level].Lx.ptr<float>(y2)+x1);
res4 = *(evolution[level].Lx.ptr<float>(y2)+x2);
rx = (1.0-fx)*(1.0-fy)*res1 + fx*(1.0-fy)*res2 + (1.0-fx)*fy*res3 + fx*fy*res4;
res1 = *(evolution[level].Ly.ptr<float>(y1)+x1);
res2 = *(evolution[level].Ly.ptr<float>(y1)+x2);
res3 = *(evolution[level].Ly.ptr<float>(y2)+x1);
res4 = *(evolution[level].Ly.ptr<float>(y2)+x2);
ry = (1.0-fx)*(1.0-fy)*res1 + fx*(1.0-fy)*res2 + (1.0-fx)*fy*res3 + fx*fy*res4;
// Get the x and y derivatives on the rotated axis
rry = gauss_s1*(rx*co + ry*si);
rrx = gauss_s1*(-rx*si + ry*co);
// Sum the derivatives to the cumulative descriptor
dx += rrx;
dy += rry;
mdx += fabs(rrx);
mdy += fabs(rry);
}
}
// Add the values to the descriptor vector
gauss_s2 = gaussian(cx-2.0f,cy-2.0f,1.5f);
kpt.descriptor[dcount++] = dx*gauss_s2;
kpt.descriptor[dcount++] = dy*gauss_s2;
kpt.descriptor[dcount++] = mdx*gauss_s2;
kpt.descriptor[dcount++] = mdy*gauss_s2;
len += (dx*dx + dy*dy + mdx*mdx + mdy*mdy)*gauss_s2*gauss_s2;
j += 9;
}
i += 9;
}
// convert to unit vector
len = sqrt(len);
for(int i = 0; i < dsize; i++)
{
kpt.descriptor[i] /= len;
}
if( USE_CLIPPING_NORMALIZATION == true )
{
Clipping_Descriptor(kpt,CLIPPING_NORMALIZATION_NITER,CLIPPING_NORMALIZATION_RATIO);
}
}
在下一节,我们将介绍 KAZE 算法在 OpenCV 中的使用方法,并与其它 OpenCV 包含的特征检测算法进行简要的比较。
待续...
Ref:
[6]Brown, M., Lowe, D.: Invariant features from interest point groups. In: British Machine Vision Conf. (BMVC), Cardiff, UK (2002) http://www.cs.ubc.ca/~lowe/papers/brown02.pdf
[7]Pablo F. Alcantarilla, Luis M. Bergasa and Andrew J. Davison, Gauge-SURF Descriptors, Image and Vision Computing 31(1), 2013. http://www.robesafe.com/personal/pablo.alcantarilla/papers/Alcantarilla13imavis.pdf (Source code: http://www.robesafe.com/personal/pablo.alcantarilla/code/opengsurf_1_0.rar )