根据 rubic 打分。
1.
我认为,如果说明 m, n 是自然数,所以最小值是 1 会更清楚。所以 Clarity 我给了 3 分。其他都是 4 分,所以一共是 23 分。
2. 
我给出的分数 0 + 4 + 4 + 4 + 4 + 0。
明显可以看出是计算错误,但由于目前是考察数学思考,并不需要像工程师一样精确。所以这个被视为 slip。
Logical correctness: 2 分。逻辑正确但是计算错误。
Overall valuation: 2 分。同理,逻辑正确但是计算错误。
3. 
我给出的分数:4 + 3 + 4 + 3 + 4 + 2 = 20
下结论那里写的是 n(n+1) 而实际上应该是 n^2 + n + 1。
所以, clarity 是 3分,需要花一点点来弄清楚结论。
State conclusion 是 3 分,需要花一点点来弄清楚结论。
Overall valuation 是 2 分。The answer is fairly good, but there is room for improvement.
4. 
没有理解题意,0分。
5. 
我给出的分数:4 + 4 + 3 + 0 + 4 + 2
开头的结论,少了理由 "By the Division Theorem"
Clarity: 开头的结论,少了理由 "By the Division Theorem",所以给 3 分。你不说原因,会令人困惑。
Opening: 3 分。同样的理由
State conclusion:3 分。有隐含提到,我认为给 2 分就够了。
Reasons:0分。同样的理由,因为缺少重要的理由(前提)。
Overal: 2 分。有提升空间。
4 + 3 + 3 + 3 + 0 + 2 = 15
6. 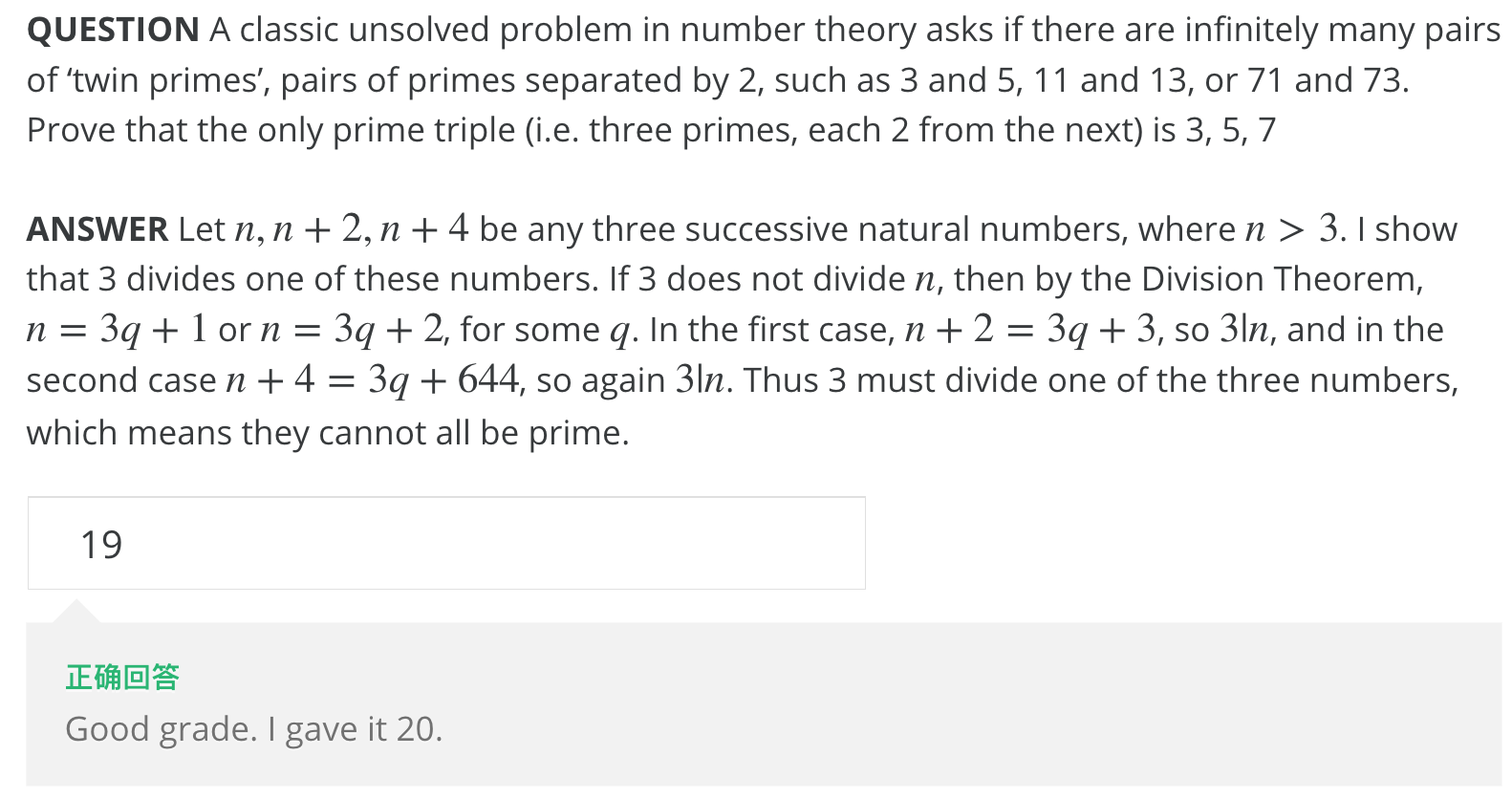
我的评分:4 + 4 + 3 + 2 + 4 + 2
评分存在问题,Opening 中,引用了 Division Theorem,给 4 分。State conclusion 给 4 分,"they can not all be prime"。

虽然存在很多 typos,但是逻辑是正确的。但对于我来说,这些 typo 让我花费更多去理解,所以 Clarity 给 2 分,Overall valuation 给 2 分。
7.

我给出的评分:4 + 4 + 4 + 0 + 4 + 2
在 "Assume it hold for n. Then" 之后,少了 "adding 2^(n+1) to both side of the assumed identity",所以会令人很困惑。由于这个
Clarity: 2 分
Reasons: 2 分
Overall valuation: 2 分
其他都是 4 分。至于我认为的没有陈述结论,其实逻辑上已经完整了。"The result(assumption) follows by induction"。所以总分相同,可能错的更离谱。
8. 
我给出了满分。
Instructor 认为:"Pick epsolon > 0" 会让初学者困惑,应该换成 "Let epsolon > 0 be given",因为这个 proof 是写给人看的,目标群体是初学者。
最后的结论少了 "by definition of limits"。
所以 Clarity, Opening, Reasons, Overall Valuation 都是 3 分。总分为 20。
9. 
我给出的评分:4 + 3 + 4 + 3 + 3 + 4
对于初学者来说,还需要证明趋近于 0 为什么交集是空集。所以 Clarity 是 3 分,Reasons 是 2 分,Overall valuation 是 3 分。
10.
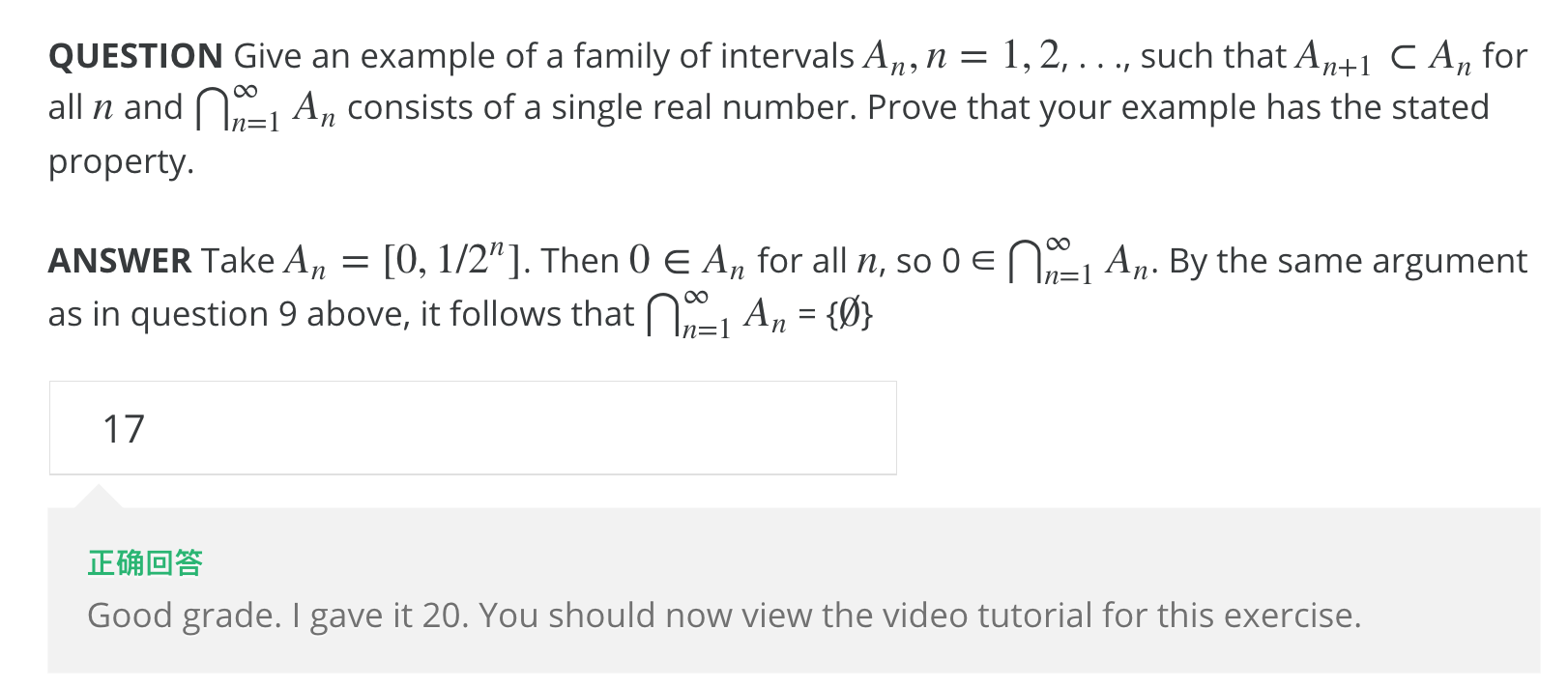
和上一题一样。