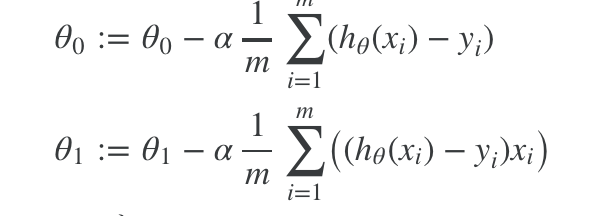Machine Learning

Matrix 定义及基本运算

Transposing

To "transpose" a matrix, swap the rows and columns.

We put a "T" in the top right-hand corner to mean transpose:

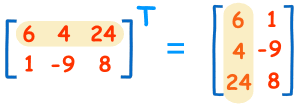
Inverse of matrix

The Inverse of A is A^-1 only when:

A × A^-1 = A^-1 × A = I

Sometimes there is no Inverse at all.

Line Regression Model and Cost Function

m: 训练集的数量；

X: 输入的训练集

y：输出

(x⁽ⁱ⁾, y⁽ⁱ⁾)：第 i 个训练集

Cost Function

确定了 h_θ(x) = θ₀ + θ₁x，那么如何选择 θ？

选择合适的 θ 使 h_θ(x) 可以靠近 y 在我们的训练集数据中。h_θ(x) 靠近 y 用数学形式表示为 。，在前面加上 1/m，表示平均值。再除以2，平均值的一半。所以最后变为 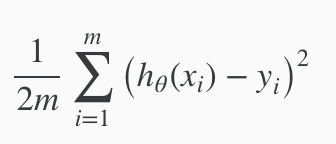。理论上来说，1 / 2m 不影响函数的趋势。但是加上之后可以排除 m 的影响，获取数据偏差大小，便于比较、观察。

比较 h_θ(x) 和 J(θ)

h_θ(x) 是对 y 的预测。当 θ 固定时才存在。h_θ(x) 为纵坐标，X 为横坐标。

J(θ) 是 cost function，计算不同 θ 情况下，预测与实际的偏离程度。J(θ) 为纵坐标，θ 为横坐标。

Gradient decent（梯度下降）

上一节提到，cost function 是随着 θ 变化的，所以要找到 cost function 的最小值，就要改变 θ。就由本函数来完成。

1. 从一组 θ 的初始值开始
2. 不断改变 θ 的值直到我们找到了期望的最小值

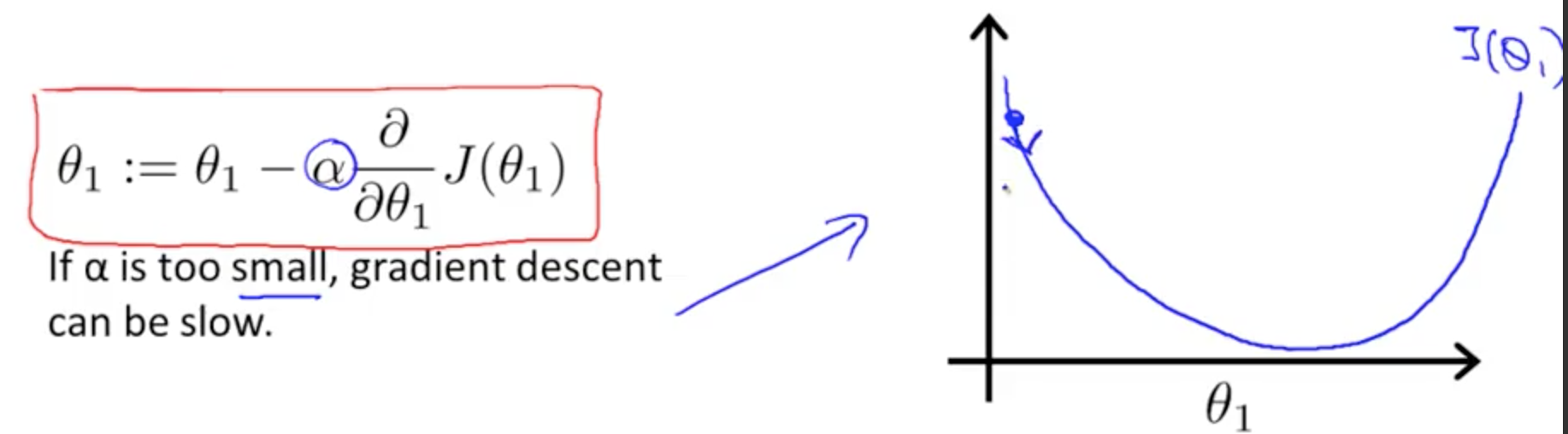
α 是学习速率。右图中学习速率 * 斜率是正数，可知 θ 是逐渐减小的。

梯度下降能够到达最低点，即使学习速率是固定的。由于越接近最低点，斜率越小。所以，不需要随着时间减小 α。

Gradient Decent For Linear Regression

上节介绍了 Gradient Decent 的是什么，这里介绍其与 Linear Regression 的结合。

 h_θ(x) = θ₀ + θ₁x

对 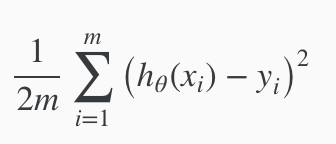，对 θ₀ 求导变为 ；

对 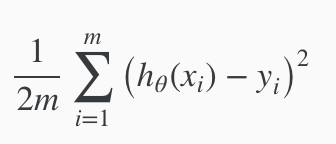，对 θ₁ 求导变为 （复合函数求导）；

 

参考

导数