树的遍历
递推公式
X序遍历,就先打印X,再打印左右
前序遍历的递推公式:
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式(有序):
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式:
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
package algo
import (
"fmt"
"testing"
)
type Node struct {
data int
left *Node
right *Node
}
func PreOrder(node *Node){
if node == nil{
return
}
fmt.Println(node.data)
PreOrder(node.left)
PreOrder(node.right)
}
//从小到大有序
func InOrder(node *Node){
if node == nil {
return
}
//递归找到最左(最小的点)
InOrder(node.left)
fmt.Println(node.data)
InOrder(node.right)
}
func PostOrder(node *Node){
if node == nil{
return
}
PostOrder(node.left)
PostOrder(node.right)
fmt.Println(node.data)
}
func TestTree(t *testing.T){
tree := &Node{data:5}
tree.left = &Node{data:4}
tree.right = &Node{data:7}
tree.left.left = &Node{data:3}
PostOrder(tree)
}
func FindValue(root *Node,value int) *Node{
//以根节点为起点
currentNode := root
//叶节点指针为空
for currentNode != nil{
//数值相同,直接返回
if currentNode.data == value{
return currentNode
//数值比当前节点大,节点偏移到当前节点的右节点
}else if value > currentNode.data {
currentNode = currentNode.right
}else if value < currentNode.data {
currentNode = currentNode.left
}
}
//没有找到返回空指针
return nil
}
/**
关键:
1. 树是空的判断
2. 插入位置节点是空的判断
*/
func insert(tree *Node,value int){
//树是空的,直接把根节点指向新插入数据
if tree == nil{
tree = &Node{data:value}
return
}
currentNode := tree
//遍历到叶子节点
for currentNode != nil{
//如果新数据比当前节点大,并且右节点为空,则插入到右节点
if value > currentNode.data{
if currentNode.right == nil{
currentNode.right = &Node{data:value}
return
}
//右节点不为空,继续从右节点找插入位置
currentNode = currentNode.right
}else{
if currentNode.left == nil{
currentNode.left = &Node{data:value}
return
}
currentNode = currentNode.left
}
}
}
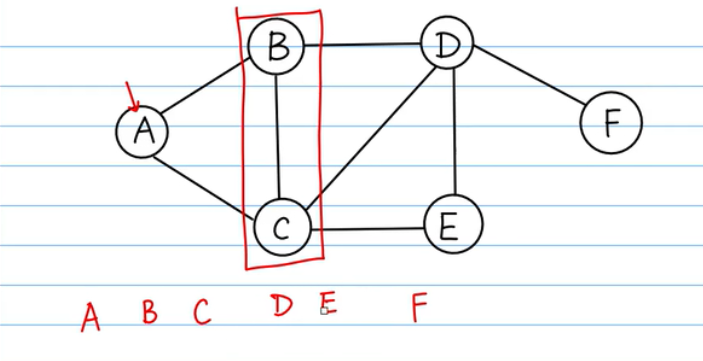
BFS
- 图其实是树的一个变种
- 从A出发,一层一层从左到右,从上往下
- 先遍历与A相邻的节点(B & C,顺序无要求,可以多种结果)
- 从左到右看和B & C相邻的节点
- 由于先遍历的是B,先求B相邻的节点(A C D),由于A C已经遍历过,只需要遍历D
数据结构
- 队列(A入队,A出队,并且把A相邻节点B C塞入队列。把B拿出来同时把B的相邻节点D塞入队列...可以保证先遍历B再遍历C的节点),用队列保证下一个遍历的元素是前面元素的顺序
DFS
- 从A出发,一条路走到底,再往回走
- 先找一个与A相邻的点(B or C)B
- 再找与B相邻的点(C or D)D
- 找与D相邻的点(C or E or F)F
- 发现F没有路,往回挑到前面一个点(D)
- 找D没有走过的点(C or E)E
- 从E找没有做过的点C
- C发现所有点已经走完(回跳)

数据结构
- 栈(A入栈,把栈里清空一个元素并把邻节点放入,C和B入栈,B出栈,把B的邻节点,D入栈...F没有邻节点,也要从栈拿出一个元素),用栈保证下一个拿的是上一个元素的邻节点
package algo
import (
"testing"
)
func BFS(graph map[string][]string,start string)[]string{
//初始化队列,起点入队
queue := []string{}
queue = append(queue, start)
//初始化访问集合,起点加入集合
visitedSet := map[string]bool{}
visitedSet[start] = true
//用一个切片记录走过的路径
bfs := []string{}
//循环,直到队列无元素(最后一个点)
for len(queue) > 0 {
//取出队头
vertex := queue[0]
queue = queue[1:]
//记录路径
bfs = append(bfs, vertex)
//取出队头的邻节点
neighbor := graph[vertex]
//队头的未访问的邻节点全部入队,并且放到访问集合
for _,node := range(neighbor){
if !visitedSet[node]{
queue = append(queue,node)
visitedSet[node] = true
}
}
}
return bfs
}
func DFS(graph map[string][]string,start string){
//建立栈,并且起点入栈
stack := []string{}
stack = append(stack,start)
//建立已访问集合,并且标记起点已访问
visitedSet := map[string]bool{}
visitedSet[start] = true
//循环,结束点是栈中没有元素
for len(stack) > 0 {
//取出栈顶(数组最后一个元素)
vertex := stack[len(stack)-1]
stack = stack[:len(stack)-1]
//取出栈顶元素的邻节点
neighbors := graph[vertex]
fmt.Println(vertex)
//循环邻节点的所有元素
for _,node := range(neighbors){
//判断元素,如果没有被访问,则入栈并标记为已访问
if !visitedSet[node]{
stack = append(stack,node)
visitedSet[node] = true
}
}
}
}
func TestBFS(t *testing.T){
graph := map[string][]string{}
graph["A"] = []string{"B","C"}
graph["B"] = []string{"A","C","D"}
graph["C"] = []string{"A","B","D","E"}
graph["D"] = []string{"B","C","E","F"}
graph["E"] = []string{"C","D"}
graph["F"] = []string{"D"}
bfs := BFS(graph,"A")
t.Log(bfs)
}
堆
特点
- 是完全二叉树,除了最后一层,数据都是满的,最后一层靠左
- 节点的值大于或小于左右节点
- 最大值在顶点的是大顶堆,最小值在顶点的是最小堆
- 数组存储,节点i,左节点i2,右节点i2+1
建堆和移除堆顶
建堆:把节点插入到末尾,从下向上,每个节点与父节点比较,不满足大小关系就交换(从下往上是指节点主动与父节点比较),直到节点循环到1为止
移除堆顶:用节点最后一个值覆盖堆顶的值,然后进行堆化,从堆顶开始,从上往下,每个父节点与左边节点比较,如果不满足大小关系,则把最大标记置为左节点,右节点同理。通过两个比较后,如果最大标记仍然是父节点,表示满足了大小关系,循环结束,否则父节点与最大标记交换。父节点更新为最大标记的位置,开始下一轮比较。
type Heap struct {
arr []int
count int //已使用的容量
length int //总容量
}
//模拟构造函数
func NewHeap(length int)*Heap{
heap := &Heap{}
heap.arr = make([]int,length+1) //初始化,从arr[1]开始使用
heap.count = 0 //默认已使用容量为0
heap.length = length+1
return heap
}
func (this *Heap)insert(value int){
//已使用容量 >= 总容量 表示容量已满
if this.count >= this.length{
return
}
//标记已使用容量+1
this.count++
//最后一个元素放入value
this.arr[this.count] = value
//从下往上堆化(子节点主动跟父节点比较)
i := this.count
//循环结束条件:i/2>0表示最后一直比较到1
//子节点与父节点比较
for i/2 > 0 && this.arr[i] > this.arr[i/2]{
this.arr[i], this.arr[i/2] = this.arr[i/2], this.arr[i]
//i偏移到父节点,如果比较不成立,表示不需要移动数据,数据已经到了合适的位置
i = i / 2
}
}
func (this *Heap)removeMax(){
if this.count == 0{
return
}
//用最后一个值覆盖第一个值
this.arr[1] = this.arr[this.count]
//总数减少
this.count--
//堆化
this.heapify()
}
func (this *Heap)heapify(){
//从第一个节点开始比较
i := 1
for {
//假设父节点是最大的
maxPos := i
//当左节点存在(小于和等于都是存在的),比较大小,如果左节点更大,maxPos更新为左节点的值
if i*2 <= this.count && this.arr[i] < this.arr[i*2]{
maxPos = i*2
}
//同理,如果右节点更大,更新为右节点的值
if i*2+1 <= this.count && this.arr[i] < this.arr[i*2+1]{
maxPos = i*2+1
}
//如果左右比价后,父节点仍然是最大的,表示已经不需要比较,数据都是正常的
if maxPos == i {
break
}
//否则,用父节点跟左右节点中最大的值交换
this.arr[i],this.arr[maxPos] = this.arr[maxPos],this.arr[i]
//父节点更新为最大标记的位置,以进行下一轮比较的起点
i = maxPos
}
}
func TestHeap(t *testing.T){
head := NewHeap(5)
head.insert(4)
head.insert(6)
head.insert(1)
head.insert(3)
head.insert(7)
head.removeMax()
head.removeMax()
for i:=1; i<=head.count;i++{
t.Log(head.arr[i])
}
}
堆排序
步骤
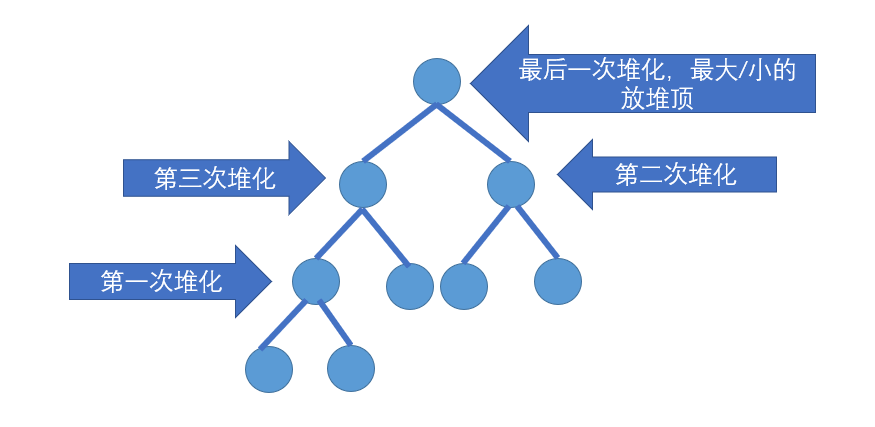
- 建堆:从n/2开始到1(非叶子节点的范围),从后往前推进,逐渐建堆(假设开始堆只有3个元素,逐渐往上加)
- 堆化:传入一个父节点以及数组结束位置,父节点与左右节点对比,如果没有交换,则父节点是最大的,否则,标记左/右节点为下一个父节点,并交换元素,并继续向下堆化
- 排序:先进行第一次建堆,建完后最大/小值在堆顶,把堆顶放到数组末尾,并且砍掉(i--),重复此过程,直到堆顶(i)
package algo
import (
"testing"
)
//堆化
func heapify(arr []int,start int,end int){
i := start
//用一个变量记录最大的位置
maxPos := i
for{
//找出父左右中最大的节点
//当左节点没有超过数组的边界并且左节点更大,标记最大位置
if i*2 <= end && arr[i*2] > arr[i]{
maxPos = i*2
}
if i*2+1 <= end && arr[i*2+1] > arr[maxPos]{
maxPos = i*2+1
}
//父节点已经是最大的时候,结束循环
if maxPos == i {
break
}
//父节点不是最大的时候,跟最大的节点交换,并且标记下一轮循环的父节点为该节点
//如果不用循环继续往下堆化,依然可找出最大的元素在父节点,但是无法保证子节点的堆性质成立
arr[maxPos],arr[i] = arr[i],arr[maxPos]
i = maxPos
}
}
func buildHead(arr []int,start int,end int){
//从最后一个非叶子节点开始,逐渐加入元素,建堆
for i:=end/2; i>=start; i--{
heapify(arr,i,end)
}
}
func heapSort(arr []int){
//从后往前堆化,完成后堆顶是最大的元素
//把堆顶的元素跟最后一个元素交换,并且往前推移,直到推进到堆顶
for i := len(arr)-1;i>=1;i--{
buildHead(arr,1,i)
arr[i],arr[1] = arr[1],arr[i]
}
}
func TestHeadSort(t *testing.T){
arr := []int{0,5,7,2,4,1}
heapSort(arr)
for i:=1; i<len(arr);i++{
t.Log(arr[i])
}
}