快速排序与随机快速排序

快速排序与随机快速排序

问题描述

    实现对数组的普通快速排序与随机快速排序。

实验要求

（1）实现上述两个算法 

（2）统计算法的运行时间

（3）分析性能差异，作出总结

算法原理

（一）快速排序

    通过使用分治思想对快速排序算法进行描述。下面对一个典型的子数组A[p…r]进行快速排序的三步分治过程：

    分解：数组A[p…r]被划分为两个（可能为空）子数组A[p…q-1]和A[q+1…r]，使得A[p…q-1]中的每一个元素都小于等于A[q]，而A[q]也小于等于A[q+1…r]中的每个元素。其中，计算下标q也是划分过程的一部分。

    解决：通过递归调用快速排序，对于数组A[p…q-1]和A[q+1…r]进行排序。

    合并：因为子数组都是原址排序的，所以不需要合并操作：数组A[p…r]已近有序。

 

关键代码实现：

（一）实现快速排序：

QUICKSORT(A,p,r)

1 if p < r

2     q = PARTITION(A,p,r)

3     QUICKSORT(A,p,q-1)

4     QUICKSORT(A,q+1,r)

 

（二）数组的划分：

PARTITION(A,p,r)

1 x = A[r]

2 i = p-1

3 for j = p to r-1

4     if A[j] <= x

5         i = i + 1

6         exchange A[i]with A[j]

7 exchange A[i+1] with A[r]

8 return i+1

 

（二）随机快速排序

    随机快速排序与始终采用A[r]作为主元的方法不同，通过采用一种随机抽样的随机化技术，使得从子数组A[p…r]中随机选择一个元素作为主元。为达到这一目的，首先将A[r]从A[p…r]中随机选出的一个元素交换。通过对序列p,…,r的随机抽样，我们可以保证主元元素x=A[r]是等概论地从子数组的r-p+1个元素中选取的，由于主元素是随机选取的，使得对输入数组的划分也是比较均衡的，从而获得较好的期望性能。 

关键代码实现：

（一）随机数组的调用：

RANDOMIZED-PARTITION(A,p,r)

1 i = RANDOM(p,r)

2 exchange A[r] with A[i]

3 return PARTITION(A,p,r)

 

（二）函数PARTITION(A,p,r)仍调用快速排序的PARTITOON(A,p,r)函数

说明：快速排序过程中，调用QUICKSORT()和PARTITION()函数进行数组内部的快速排序；对于随机快速排序，则调用RANDOMIZED-PARTITION()来选取随机的关键字（key），再通过QUICKSORT()和PARTITION()函数进行排序。

 

实验截图

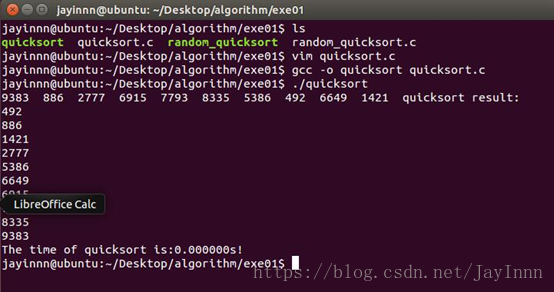
10个元素快速排序的实验结果：

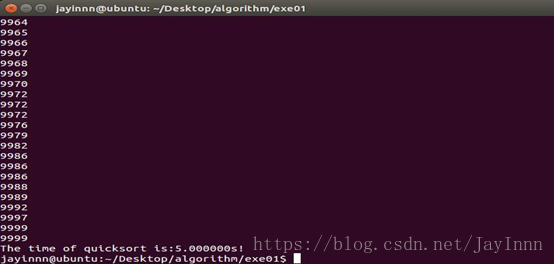
10000个元素快速排序的实验结果：

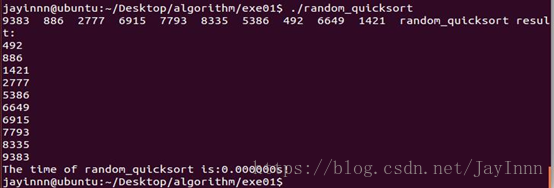
10个元素随机快速排序的实验结果：

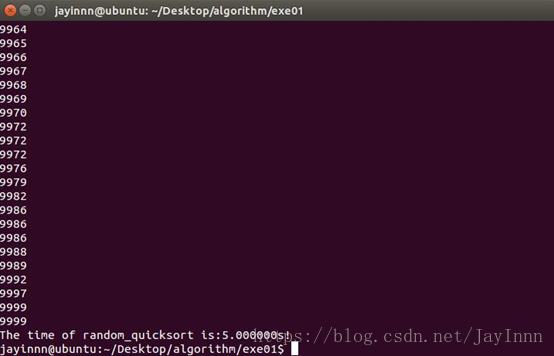
10000个元素随机快速排序的实验结果：

结果分析

（一）从原理上分析，快速排序的最坏运行时间是Θ(n²),即在每次进行PARTITION(A,p,r)函数对数组A进行划分时，都出现主元素在划分区域的某一侧，使得划分区域的元素都小于或大于主元素；期望运行时间是Θ(nlgn)，在随机快速排序中，运行RANDOMIZED_PARTITION(A,p,r)后每次选取主元素都能使得主元素在划分区域的中间。

（二）从实际的运行过程中，实验随机生成10、10000个数据进行排序，并比较了运行排序代码的时间。实验出现中，运行时间未出现较大区分度的原因：一方面是因为在普通快速排序过程中，数组是随机生成的，这样使得在每次选取主元时，和随机快速排序相似，从而二者区分度不高；另一方面，电脑主频较高、选取的实验数据不够大也会使二者区分度不高。

  

附录（代码）

（一）普通快速排序

#include <stdio.h>

#include <stdlib.h>

#include <time.h>


#define max 10000

#define CLOCKS_PRE_SEC ((clock_t)1000)


void quicksort(int array[], int p, int r)

{
    if(p < r)
    {
       int q;
       q =partition(array, p, r);
       quicksort(array,p, q-1);
       quicksort(array,q+1, r);
    }
}

int partition(int array[], int p, int r)
{
    int x,m,i,j;
    x = array[r];
    i = p-1;
    for(j = p; j<= r-1; j++ )
    {
       if(array[j]<= x)
       {
           i = i+ 1;
           m =array[i];
           array[i]= array[j];
           array[j]= m;
       }
    }
    m =array[i+1];
    array[i+1] =array[r];
    array[r] = m;
    return (i+1);
}

int main()
{
    intarray[max];
    int i = 0;
    clock_tstart,finish;
    doubleTheTimes;
    for(i = 0; i< max; i++)
    {
       array[i] =rand()%10000;
       printf("%d  ",array[i]);
    }
    printf("
quicksortresult:
");
    start =clock();
    quicksort(array,0 ,max-1);
    finish =clock();

    for(i = 0; i< max; i++)
       printf("%d
",array[i]);

    TheTimes =(double)((finish - start)/CLOCKS_PRE_SEC);
    printf("Thetime of quicksort is:%fs!
",TheTimes);

}

 

（二）随机快速排序

#include <stdio.h>

#include <stdlib.h>

#include <time.h>

 

#define max 1000

#define CLOCKS_PRE_SEC ((clock_t)1000)

 

int random_partition(int array[], int p, int r)

{

    int i,m;

    i =rand()%(r-p+1)+p;

    m = array[r];

    array[r] =array[i];

    array[i] = m;

    m =partition(array, p, r);

    return m;

}

 

void random_quicksort(int array[], int p, int r)

{

    if(p < r)

    {

       int q;

       q =random_partition(array, p, r);

       random_quicksort(array,p, q-1);

       random_quicksort(array,q+1, r);

    }

}

 

int partition(int array[], int p, int r)

{

    int x,m,i,j;

    x = array[r];

    i = p-1;

    for(j = p; j<= r-1; j++ )

    {

       if(array[j]<= x)

       {

           i = i+ 1;

           m =array[i];

           array[i]= array[j];

           array[j]= m;

       }

    }

    m =array[i+1];

    array[i+1] =array[r];

    array[r] = m;

 

    return (i+1);

}

 

int main()

{

    intarray[max];

    int i = 0;

    clock_tstart,finish;

    doubleTheTimes;

 

 

    for(i = 0; i< max; i++)

    {

       array[i] =rand()%10000;

       printf("%d  ",array[i]);

    }

    printf("random_quicksortresult:
");

 

    start =clock();

    random_quicksort(array,0 ,max-1);

    finish =clock();

 

    for(i = 0; i< max; i++)

       printf("%d
",array[i]);

    TheTimes = (double)((finish- start)/CLOCKS_PRE_SEC);

    printf("Thetime of random_quicksort is:%fs!
",TheTimes);

}