题面在最下方。
本题观察后可以发现,当两个竖线遇到横线的时候,两个竖线所代表的数字会交换位置
所以对于一根链接<x,x+1>的横线,swap(a[x],a[x+1])即可。这个是第一问
对于第二问,拿到给定的序列之后,求解逆序对即可

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 template<class _T>inline void read(_T &_a) 5 { 6 char _ch=getchar();_a=0; 7 while(_ch<'0'||_ch>'9')_ch=getchar(); 8 while(_ch>='0'&&_ch<='9'){_a=(_a<<3)+(_a<<1)+_ch-'0';_ch=getchar();} 9 } 10 11 const int maxn=100001,maxm=1000001; 12 int n,m,id[maxn],S[maxn],ans; 13 14 void merge(int l,int r) 15 { 16 if(l==r) return ; 17 int mid=l+r>>1; 18 merge(l,mid); 19 merge(mid+1,r); 20 int i=l,j=mid+1,k=l; 21 while(i<=mid&&j<=r) 22 { 23 if(id[i]>id[j]) 24 { 25 ans+=mid-i+1; 26 S[k++]=id[j++]; 27 } else S[k++]=id[i++]; 28 } 29 while(i<=mid) S[k++]=id[i++]; 30 while(j<=r) S[k++]=id[j++]; 31 for (register int i=l;i<=r;++i) id[i]=S[i]; 32 } 33 34 int main() 35 { 36 freopen("draw.in","r",stdin); 37 freopen("draw.out","w",stdout); 38 read(n); read(m); 39 for (register int i=1;i<=n;++i) id[i]=i; 40 for (register int i=1,a;i<=m;++i) read(a),swap(id[a],id[a+1]); 41 for (register int i=1;i<=n;++i) printf("%d ",id[i]); 42 merge(1,n); 43 printf(" %d",ans); 44 return 0; 45 }
【题目描述】
鬼脚图,又称画鬼脚,在日本称作阿弥陀签,是一种经典游戏,也是一种简易的决策方法,常常用来抽签或决定分配组合。
下图就是一张鬼脚图,其包含若干条竖线和若干条横线。请注意,横线只能水平连接相邻的两条竖线,且 在同一高度只会有一条横线。
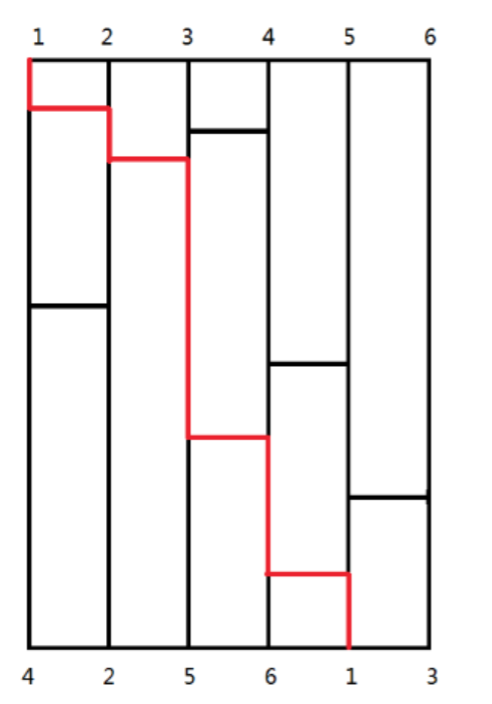
在图的上方,我们将这 n条竖线依次标号为 1 到 n。以数字 3为例,它会沿着所在的竖线下降,期间如果 遇到横线就会移动到横线的另一端,最终降落至下面的第一条竖线。上图中还标出了另外几种数字的最终位置。奇特的是,开始时每条竖线上都有一个数字,而 最终每条竖线下还是有一个数字。
现在,相信你一定已经理解了鬼脚图的规则,那么我们想请你完成下面的两个任务——
- 读入一张有 n条竖线和 m条横线的鬼脚图,请你输出最下面一行的最终序列。
- 如果让你设计一个鬼脚图最终序列达到上面的效果,你 最少需要多少条横线。
输入格式
第一行 2 个数字 n,m,表示竖线和横线的数量。
第二行 m 个数字,依次表示从高到低的横线。数字 a的意义为,在第 a(1≤a<n) 条竖线和第 a+1条竖线间存在一条横线。
输出格式
第一行 n 个数字,表示该鬼脚图的最终序列。
第二行 1 个数字,表示最少需要多少条横线。
数据范围
对于10% 的数据: n≤3,m≤5。
对于 20% 的数据: n≤4,m≤100。
对于40% 的数据:n≤8,m≤1000。
对于 60% 的数据: n≤1000,m≤5000。
对于100% 的数据:n≤100000,m≤1000000。
样例输入
3 3
1 2 1
样例输出
3 2 1
3
