【题目描述】
辣鸡ljhNOI之后就退役了,然后就滚去学文化课了。
然而在上化学课的时候,数学和化学都不好的ljh却被一道简单题难住了,受到了大佬的嘲笑。
题目描述是这样的:在一个二维平面上有一层水分子,请问形成了多少个氢键?
这个二维平面可以看做一个类似棋盘的东西,每个格子可以容纳一个水分子,左下角的格子为(0,0),这个格子右边的格子为(1,0),上方格子为(0,1),以此类推。
辣鸡ljh当然不会做了,所以他来求助JeremyGou,JeremyGou一眼就看穿了真相,并想用这道题来考一考正在做NOIP模拟赛的你。
注:在本题中,我们认为一个水分子能与和它曼哈顿距离为2且直线距离小于2的其他格子形成氢键。
【输入格式】
一个整数n接下来n行,每行给出四个整数x1,y1,x2,y2表示以(x1,y1)为左下角,(x2,y2)为右上角的矩形中每个格子都有一个水分子。给出的所有矩形没有交集。
【输出格式】
一个整数,表示氢键的数量。
【样例1输入】
3
0 0 0 0
0 1 1 2
2 2 2 3
【样例1输出】
5
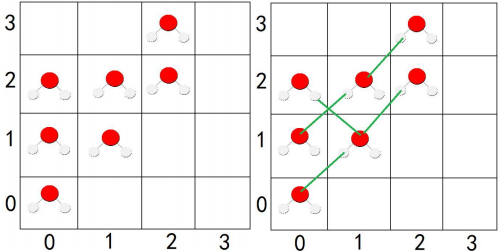
【样例1解释】左图为水分子的排布,右图中的绿色线条表示氢键。
【样例2输入】
10
1 8 8 9
0 3 10 7
0 0 7 0
0 2 9 2
4 10 8 10
10 0 10 2
0 10 0 10
8 0 9 1
0 8 0 9
9 8 10 8
【样例2输出】
157
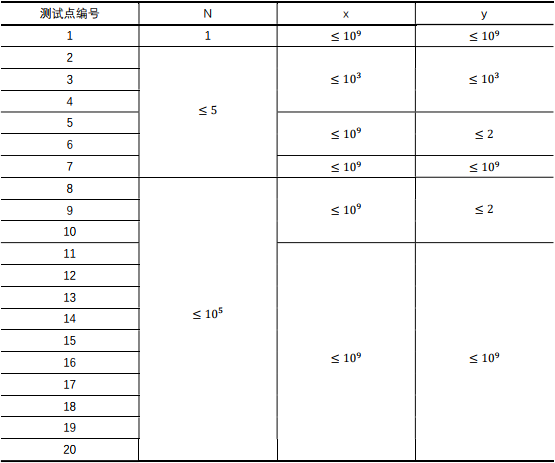
【子任务】
解题思路
本题主要是注意细节问题。我们分成两块来求,第一块是矩形内的氢键数量,第二块是矩形与矩形之间的氢键数量
一、矩形内的氢键数量
对于一个矩形【X1,Y1,X2,Y2】,我们可以通过计算得到其中的氢键数量为 (X2-X1)*(Y2-Y1)*2 (读者可以把【左上-右下】与【右上-左下】两个方向分开计算,各自都是(X2-X1)*(Y2-Y1)个氢键)
证明?请画图感性证明。
二、矩形间的氢键数量
我们先把所有矩形按照x1为关键字排序,然后O(n2)地询问,注意剪枝即可。实际复杂度约为O(NlogN)。
排序是为了方便剪枝。
剪枝:
设当前正在把 i 与 v 两个矩形进行比较,第一个for循环是i,第二个for循环是v,那么就有:
if(matrix[v].x1>matrix[i].x2+1) break;
if(matrix[v].y1>matrix[i].y2+1||matrix[v].y2<matrix[i].y1-1) continue;
如果以上两步都没有跳转,那么说明v与i一定会形成至少一个氢键。
下面就开始复杂的计算啦:
我们首先把两个矩形i、v按照 matrix[v].x1<=matrix[i].x2 的真假分为两类:
1)若此式为真,那么两个矩形一定是上下排列且连有氢键的。
2)若此式为假,那么两个矩形一定是左右排列且连有氢键的。
(因为题目描述明确说明所给矩形不会产生覆盖的情况)
这里挑一种来讨论,对于另一种我们把推导出的代码中x和y互换即可(想一想,为什么可以这样?)。
呈上对于左右排列讨论y的代码,其中对于每一种情况,读者可以自行画图体会,若读者不会位运算,可以把 <<1 等价转化为 *2 阅读。
if(matrix[v].y1>matrix[i].y2||matrix[v].y2<matrix[i].y1) ++ans; else if(matrix[v].y1==matrix[i].y1) { if(matrix[v].y2==matrix[i].y2) ans+=(matrix[v].y2-matrix[v].y1)<<1; else if(matrix[v].y2<matrix[i].y2) ans+=((matrix[v].y2-matrix[v].y1)<<1)+1; else ans+=((matrix[i].y2-matrix[i].y1)<<1)+1; } else if(matrix[v].y2==matrix[i].y2) { if(matrix[v].y1>matrix[i].y1) ans+=((matrix[v].y2-matrix[v].y1)<<1)+1; else ans+=((matrix[i].y2-matrix[i].y1)<<1)+1; } else if(matrix[v].y1>matrix[i].y1&&matrix[v].y2<matrix[i].y2) ans+=(matrix[v].y2-matrix[v].y1+1)<<1; else if(matrix[v].y1>matrix[i].y1&&matrix[v].y2>matrix[i].y2) ans+=(matrix[i].y2-matrix[v].y1+1)<<1; else if(matrix[v].y1<matrix[i].y1&&matrix[v].y2>matrix[i].y2) ans+=(matrix[i].y2-matrix[i].y1+1)<<1; else /*if(matrix[v].y1<matrix[i].y1&&matrix[v].y2<matrix[i].y2)*/ ans+=(matrix[v].y2-matrix[i].y1+1)<<1; //最后一定只剩下这种情况,为了加速程序运行,可以不再判断
对于判断x的情况,我们把上述代码中的所有“y”字符替换为“x”字符即可。
需要注意的是,由于我们已经按照x1的大小从小到大进行了排序,所以可以不再判断 matrix[v].x1<matrix[i].x1 这一种情况及其子情况。
(记得加上前文说过的两个if剪枝优化,不然你这个是妥妥的O(n2),绝对过不了!)
附上AC代码

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 template<class T>inline void read(T &_a) 5 { 6 char _ch=getchar();_a=0; 7 while(_ch<'0'||_ch>'9') _ch=getchar(); 8 while(_ch>='0'&&_ch<='9'){_a=(_a<<3)+(_a<<1)+_ch-'0';_ch=getchar();} 9 } 10 11 int n; 12 long long ans; 13 struct fff{ 14 long long x1,y1,x2,y2; 15 inline bool operator < (const fff x) const {return x1==x.x1?y1<x.y1:x1<x.x1;} 16 }node[100001]; 17 18 int main() 19 { 20 freopen("ljh.in","r",stdin); 21 freopen("ljh.out","w",stdout); 22 read(n); 23 for(register int i=1;i<=n;++i) 24 { 25 read(node[i].x1),read(node[i].y1),read(node[i].x2),read(node[i].y2); 26 ans+=(node[i].x2-node[i].x1)*(node[i].y2-node[i].y1)<<1; 27 } 28 sort(node+1,node+n+1); 29 for (register int i=1;i<n;++i) 30 { 31 for (register int v=i+1;v<=n;++v) 32 { 33 if(node[v].x1>node[i].x2+1) break; 34 if(node[v].y1>node[i].y2+1||node[v].y2<node[i].y1-1) continue; 35 if(node[v].x1<=node[i].x2) 36 { 37 if(node[v].x1==node[i].x1) 38 { 39 if(node[v].x2==node[i].x2) ans+=(node[v].x2-node[v].x1)<<1; 40 else if(node[v].x2<node[i].x2) ans+=((node[v].x2-node[v].x1)<<1)+1; 41 else ans+=((node[i].x2-node[i].x1)<<1)+1; 42 } 43 else if(node[v].x2==node[i].x2) 44 { 45 if(node[v].x1>node[i].x1) ans+=((node[v].x2-node[v].x1)<<1)+1; 46 else ans+=((node[i].x2-node[i].x1)<<1)+1; 47 } 48 else if(node[v].x2<node[i].x2) ans+=(node[v].x2-node[v].x1+1)<<1; 49 else /*if(node[v].x1>node[i].x1&&node[v].x2>node[i].x2)*/ ans+=((node[i].x2-node[v].x1+1)<<1); 50 } else { 51 if(node[v].y1>node[i].y2||node[v].y2<node[i].y1) ++ans; 52 else if(node[v].y1==node[i].y1) 53 { 54 if(node[v].y2==node[i].y2) ans+=(node[v].y2-node[v].y1)<<1; 55 else if(node[v].y2<node[i].y2) ans+=((node[v].y2-node[v].y1)<<1)+1; 56 else ans+=((node[i].y2-node[i].y1)<<1)+1; 57 } 58 else if(node[v].y2==node[i].y2) 59 { 60 if(node[v].y1>node[i].y1) ans+=((node[v].y2-node[v].y1)<<1)+1; 61 else ans+=((node[i].y2-node[i].y1)<<1)+1; 62 } 63 else if(node[v].y1>node[i].y1&&node[v].y2<node[i].y2) ans+=(node[v].y2-node[v].y1+1)<<1; 64 else if(node[v].y1>node[i].y1&&node[v].y2>node[i].y2) ans+=(node[i].y2-node[v].y1+1)<<1; 65 else if(node[v].y1<node[i].y1&&node[v].y2>node[i].y2) ans+=(node[i].y2-node[i].y1+1)<<1; 66 else /*if(node[v].y1<node[i].y1&&node[v].y2<node[i].y2)*/ ans+=(node[v].y2-node[i].y1+1)<<1; 67 } 68 } 69 } 70 printf("%lld",ans); 71 return 0; 72 }