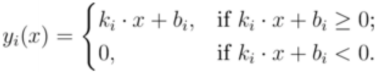polyline NOIP模拟 数论 规律

有若⼲个类似于下⾯的函数:

定义 n 个函数 y1(x), ..., yn(x) 的对于任意 x 的总和 s(x) = y1(x) + ... + yn(x)，很容易发现 s(x) 的 图像是多段线组成。给你 n 个函数，你的任务是找出 s(x) 图像不等于 180 度的⾓的个数。

多模拟几次数据，我们就可以注意到这个结果仅与图像的“拐点个数”有关，而拐点个数我们是可以求到的。

首先，我们知道，对于一个y_i（x）的函数：

当k_i=0时，他对结果是没有影响的，我们在计算的时候可以省略。

当k_i≠0时，我们可以根据函数中的条件式（k_i·x+b_i≥0）得到一个拐点坐标 x=-b_i/k_i（拐点是指图像在拐点处形成了一个角，即这个角的顶点）

我们把这个拐点坐标存下来。

当我们处理完所有的（k，b）数据后，我们就得到了一系列拐点，若“一种拐点”表示拐点坐标相同的一系列拐点，那么一种拐点就会对应函数图像中的一个角（一定会形成一个不等于180°的角）。

也就是说，所有拐点去掉重复坐标之后的剩余个数，就是答案个数。

需要证明？——你的数学函数部分学得好吗？

· 怎么实现去重？

第一个，我们可以sort一次然后手动去重。

第二个，我们可以用STL中的set来实现。（set是自动去重的）

第三个，你甚至可以用map<long double,bool>来存拐点，显然这也是不会重复记录的。然后用iterator来遍历。

· 为什么是long double？

在题目涉及浮点数计算的时候，若条件足够，应尽量选择精度高的数据结构，避免精度误差导致的答案错误。（请注意，部分低级编译器不支持long double）

附上AC代码

#include<cstdio>
#include<algorithm>
using namespace std;
template<class T>inline void read(T &_a)
{
    bool f=0;char _ch=getchar();_a=0;
    while(_ch<'0'||_ch>'9'){if(_ch=='-')f=1;_ch=getchar();}
    while(_ch>='0'&&_ch<='9'){_a=(_a<<3)+(_a<<1)+_ch-'0';_ch=getchar();}
    if(f)_a=-_a;
}

const int maxn=100001;
int n,ans;
long double cnt[maxn];

int main()
{
    freopen("polyline.in","r",stdin);
    freopen("polyline.out","w",stdout);
    read(n);
    for (register int i=1,k,b;i<=n;++i)
    {
        read(k); read(b);
        if(!k) {--i; --n; continue;}
        cnt[i]=-(long double)b/(long double)k;
    }
    ans=n;
    sort(cnt+1,cnt+n+1);
    for (register int i=1;i<=n;++i)
     if(cnt[i]==cnt[i-1]) --ans;
    printf("%d",ans);
    return 0;
}