(2019年2月19日注:这篇文章原先发在自己github那边的博客,时间是2016年10月28日)
最近应该是六叔的物化理论作业要交了吧,很多人问我六叔的作业里面有两道题要怎么进行图像函数的拟合。综合起来的问题主要有两个:
1. 知道图像的准确拟合方程,但是不知道怎么拟合。(这个是本文的重点)
2. 不知道图像的准确拟合方程,也不知道怎么拟合,这个我可以稍微提供一个拟合的方向。
先从不知道图像的准确拟合方程开始吧,当你拿到一组数据时,你肯定是先看横纵坐标写的是什么,在19题的第二问里面,要求蒸发焓和热力学温度的关系,学过物化的都知道,肯定是克劳修斯-克拉贝龙方程才能出现这两个变量的关系。因此这里我们就要利用这个方程对我们的数据进行变形。$$ln(frac{p}{p^{Theta}}) = frac{Delta_{p}H^{m}}{R}(frac{1}{373}-frac{1}{T})$$
这就很明显了嘛,把我们得到的蒸气压除以标准状态下的气压,它的对数和$-1/T$成线性关系,接着就不用我说了吧。数学建模的其中一个思路是根据已有的经验公式进行改进和修正啊,因为建模也要符合基本法啊,不能随便就上个算符吧。

18题我留着后面说,先把19题的第一问的完整拟合过程在这里写一遍。
1. 根据已有的拟合形式将所需要的数据处理好,19题的公式是:$$lg(p) = A-frac{B}{T-C}$$要的自变量是热力学温度T,因变量是$log_{10}(p),先整理好,这个在Excel里面是很容易的事情。
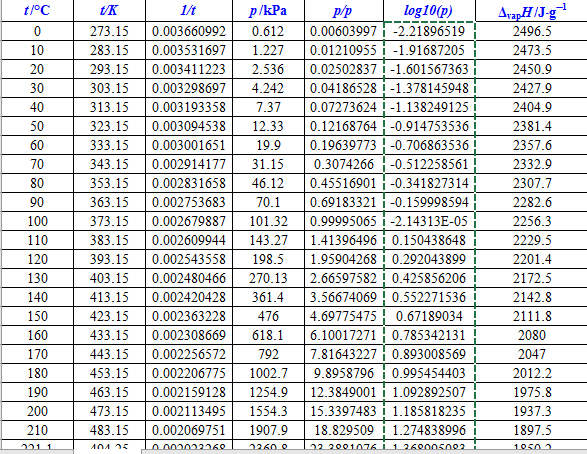
2. 打开Origin,我的是2015,不同版本操作大同小异,打开Analysis→ Fitting→ Nonlinear Curve Fit→ Open dialog。
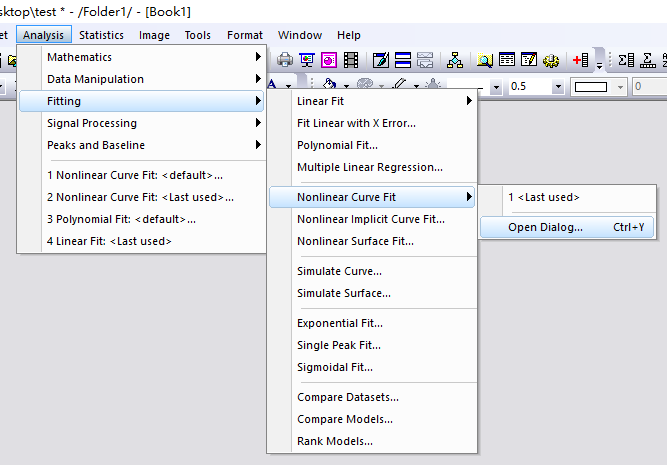
3. 在Category里面选择User Defined,可见Origin的拟合函数也是类似于Matlab的M文件一样可以自己编写。
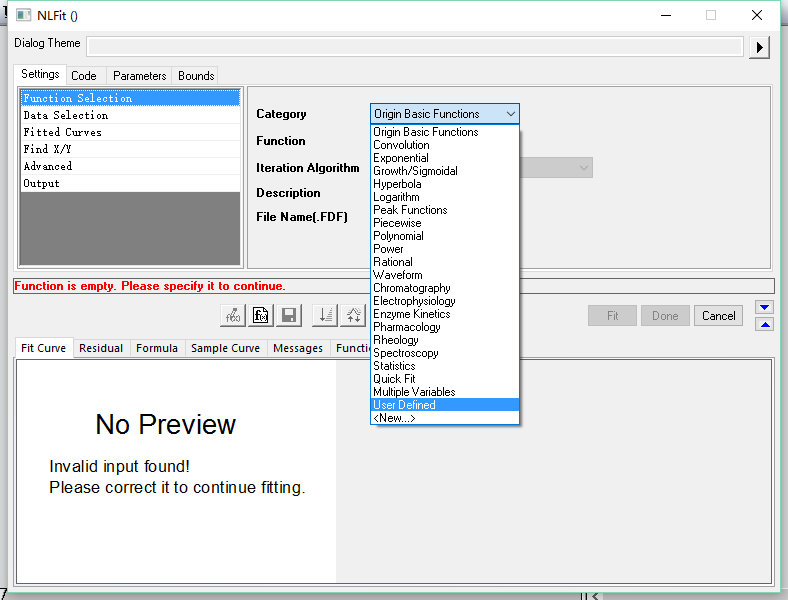
4. 当然是选择New一个函数咯,不是New一个对象。
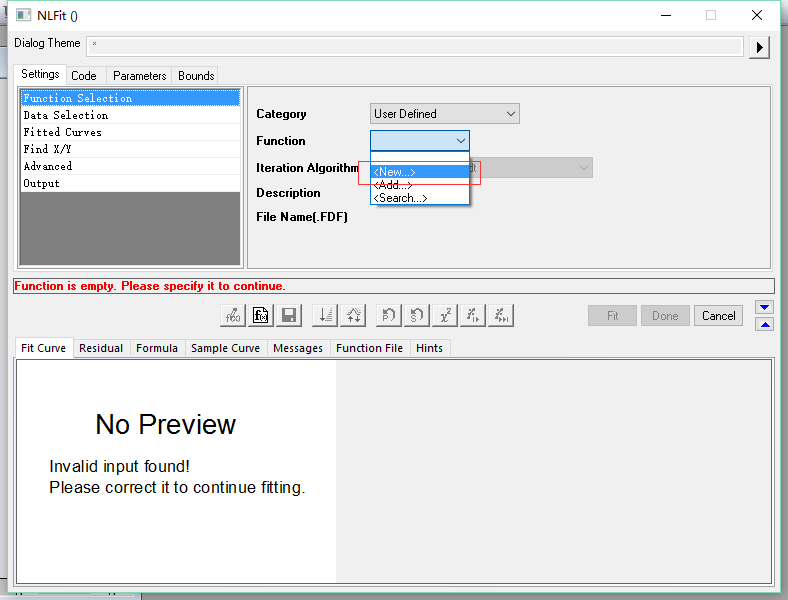
5. 从这张图开始,注意看左边的Hints,这个比网上的所谓的教程不知道高到哪里去了。从Hints中可以看到,要输入函数名,后缀名是FDF,然后是函数模型,Explicit是指明确的,Function Type是表达式,也就是所谓的y=f(x)的形式,可以看到还能选Equlations,左边的Hints告诉我们,这种类型是处理只有一个自变量的。
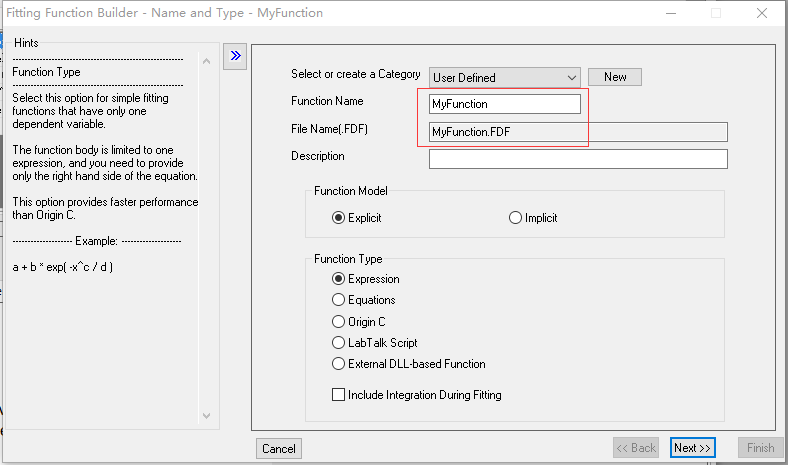
6. 点击Next,这个界面是输入自变量,因变量,参数的名字,感天谢地我的数理统计是英文版的,这里直接阅读无压力,可以看到,多个参数时用逗号分隔。
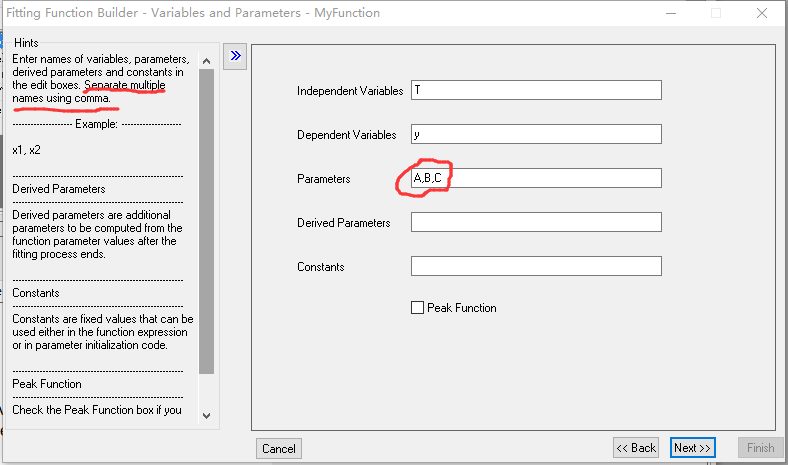
7. 这一个界面是整个过程最关键的部分,自定义函数的拟合过程中最重要的就是初值的选取,这里我们先按照要求把函数的形式输入。注意到左边的Hints,Fixed是说如果初值选取的不好的时候也不能变参数的值,显然不符合我们的意思,所以我们这里都不勾选。Fixed用在已经确定了某些参数的范围的时候。接着是初值的尝试,看到了下面的Quick Check了吗,这里是要我们选取不同的ABC作为初值,使得我们输入一个T的时候,跑出来的结果接近我们测试出来的数据值。
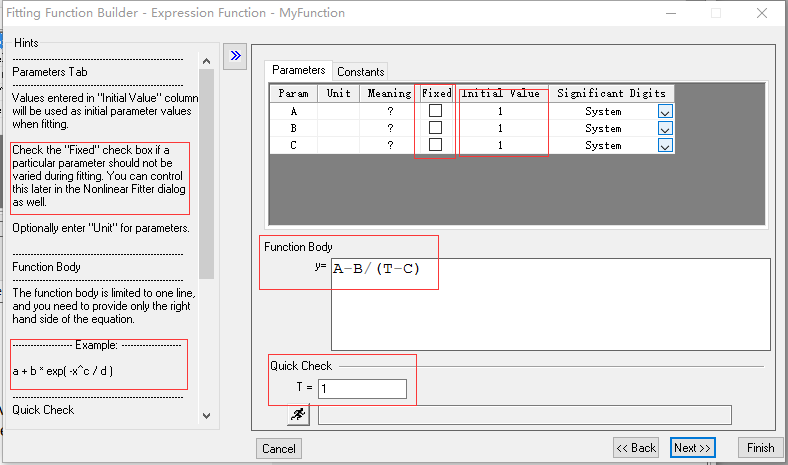
8. 经过漫长的测试,我测试出了一组值,只要接近就可以,不需要完全吻合,然后点击Next。
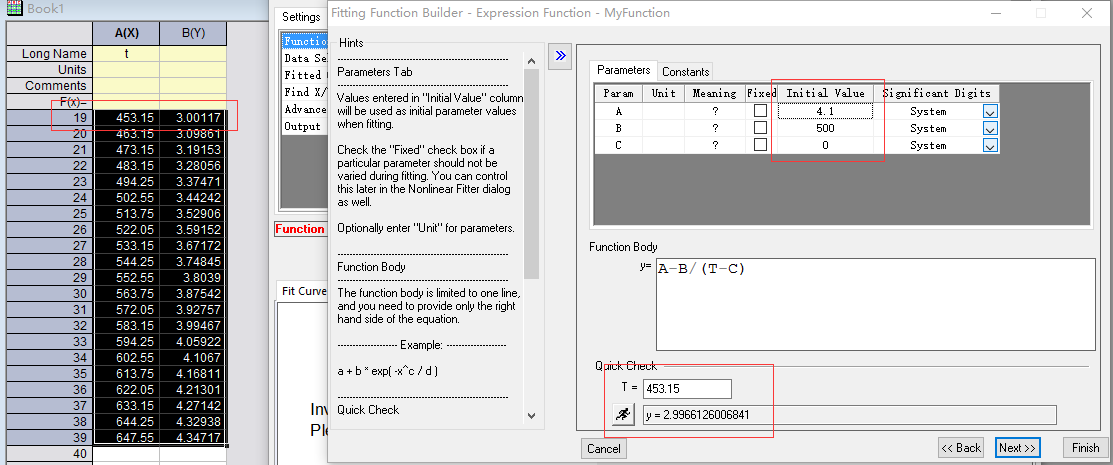
9. 这个界面也是非常的重要,刚才是测试一个点,现在就是需要将一个点变成一组数值,使得我们的函数尽可能匹配多的测试值,我们点击红色框框中的按钮,打开代码界面。
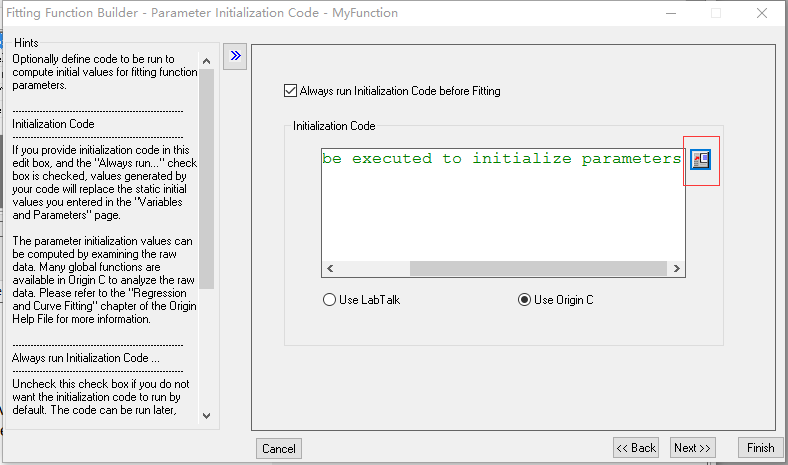
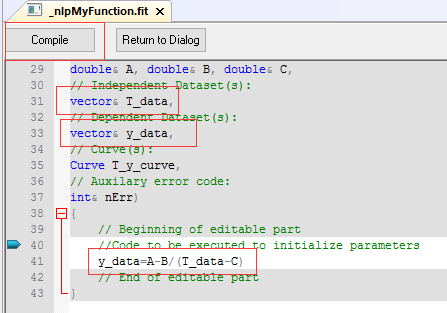
10. 看到这个界面,一股浓浓的C++代码风格袭来……,确实长的很像C++,但是又混有Matlab的风格,根据Matlab的思路,很容易就想到这个Vector存储的就是Matlab的矩阵中的值,至于这些double类型的,明显就是数字啦,这里提示我们,Code to be executed to initialized parameters,代码将在初始化参数以后执行。我们要把我们的表达式输入进去,使得vector能存储尽可能多而接近的测试值,根据变量存储的名字,很容易就知道输入的是什么东西。
11. 点击左上方的Compile,也就是编译,果然是C++风格的代码……,看到编译成功,如果失败的话请仔细检查是不是少打了什么东西,不过以逗号作为每行结尾也是反人类……
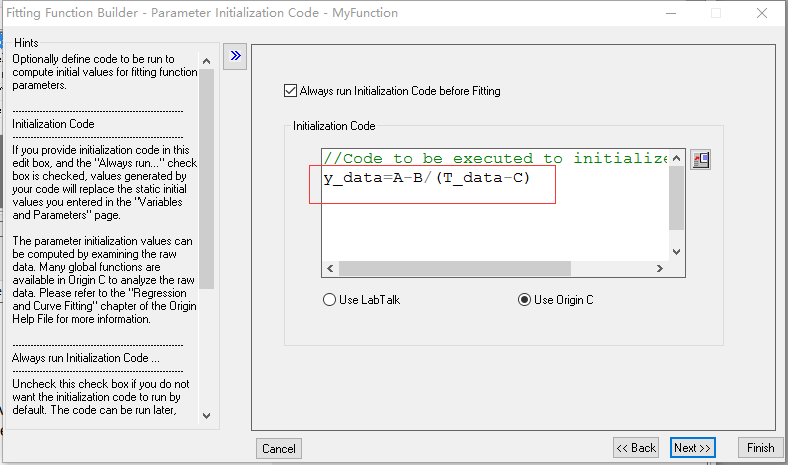
12. 然后关闭代码窗口,看到这里多来一串这样的符号,然后点击Next,一路Next直到Finish。
13. Finish以后回到这个界面,然后点击红色方框中的按钮,这个是指Fit untiled Converged,也就是根据Chi-Square Test,直到满足条件以后才能函数收敛,点击一次就可以了。可以看到提示,Fit may be Converged。
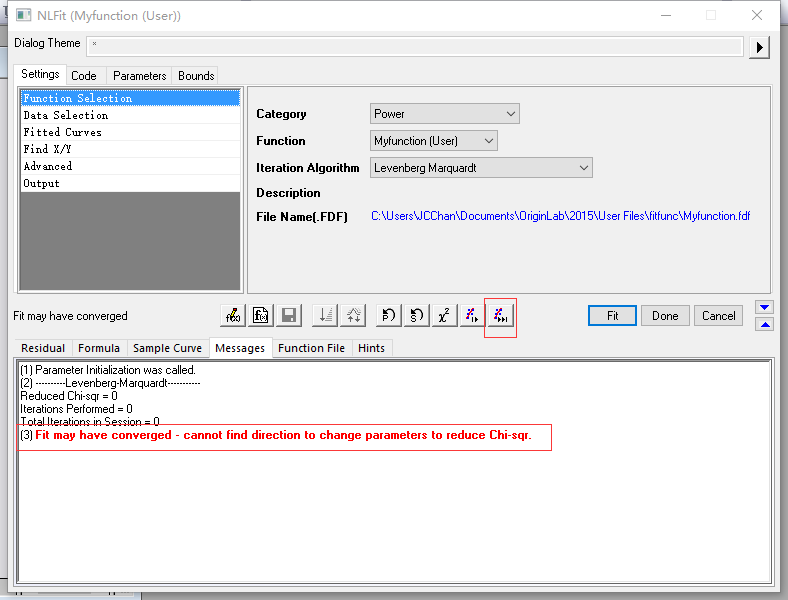
14. 点击Fit,我们就能看到一条很漂亮的拟合曲线了,R-Square还是0.99997哦,相信这个拟合应该满足要求了,接下来小伙伴就知道怎么做了吧。
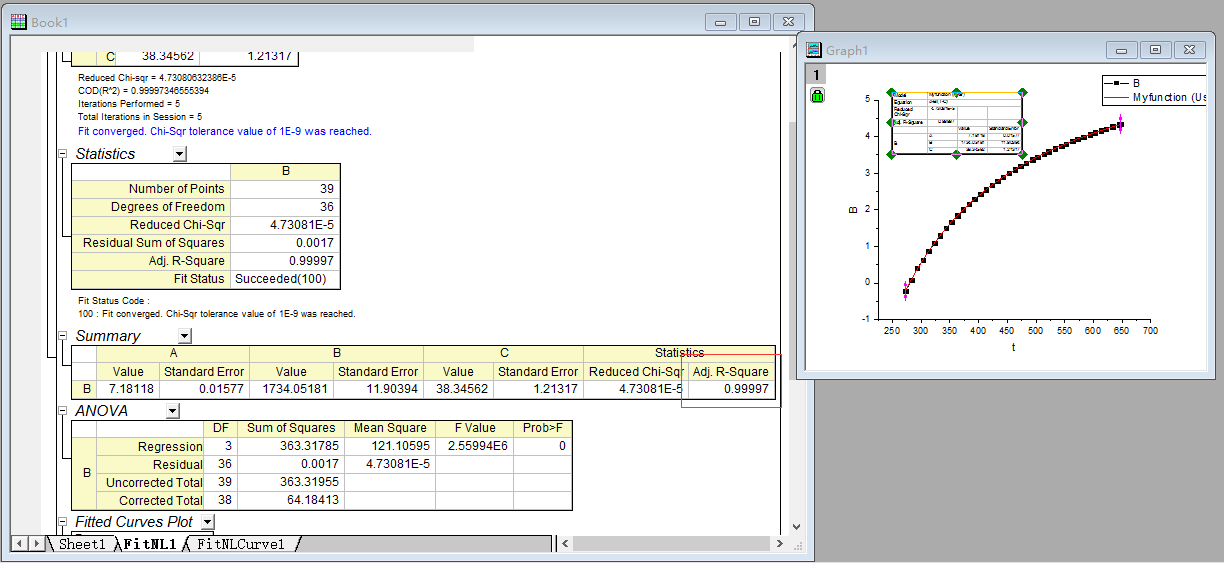
好了开始研究18题,18题里面原来是没有公式的,但是不少小伙伴拿到答案,答案里面是一种很奇怪的拟合方式,并且还有迭代什么的,其实本质上也不难,也是利用刚才的方法,只不过这里就多了好几步,其中一个是在第5步输入参数名时要把常量名字输入,这里比如说是sigma,然后在尝试初值的时候要将Constant界面的sigma的值输入为0.07275,才能开始尝试初值。

按照上述的步骤开始做自定义函数拟合,得到的界面如下。这里的Iteration Algorithm就是答案里所写的方法,不过这个Fit did not Converge是什么情况啊,我试了很多次都不行,包括答案给的初值以及自己试的初值,后来硬着头皮直接Fit,发现也能够Fit的出来,只是。
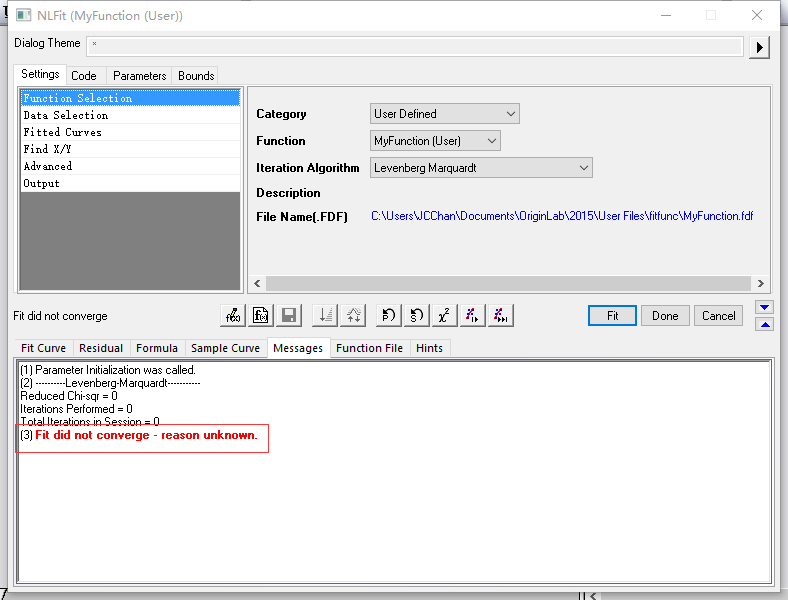
第一个是根据上述的Fit出来的结果,不觉得这个0.996瞬间low了很多了吗,而且它还是未收敛的,换句话说,肯定存在一个形式比它更好的式子满足要求。

我们回头看看式子,你看到了ln(1+x),你看到这个难道真的不会想到用泰勒展开吗,用一下不就啥问题都解决了吗,而且多项式拟合在Origin里是有快捷键的啊!
根据Analysis→ Fitting→ Polynormal Fit,随手试了2,3,4三个数,至少这3个数拟合出来的R-Square都比那个自定义函数的高,其中3又是最高的那一个,因此我们只要选3次多项式作为拟合值就好了啊,当然咯,能够用泰勒展开式的前提,是余项要趋于0,因此,泰勒展开式也不能随便乱用。
