191. 位1的个数

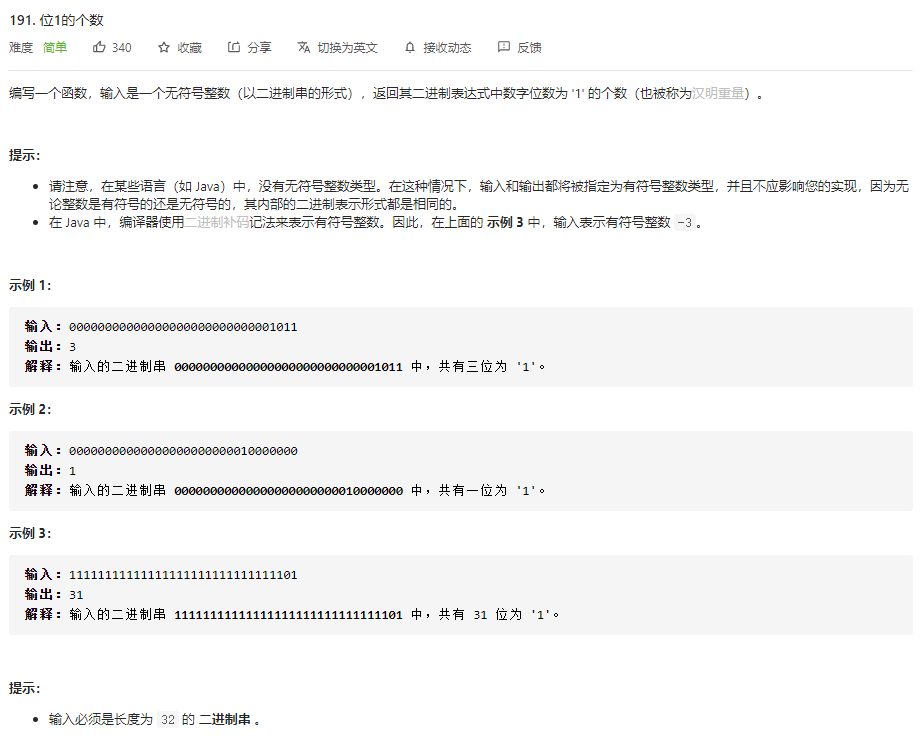
给定二进制数，要求计算该二进制数中1的个数

小知识：二进制数与int整形10进制数是可以自动转换得，如下图

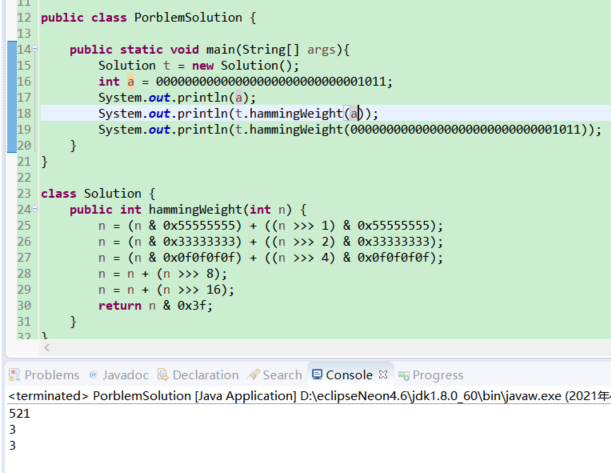
方法一：

循环检验n得每一位是否为1，时间O(k)（k为2进制数的长度，本题为32）,空间O(1)

    public int hammingWeight(int n) {
        int res = 0;
        for (int i=0;i<32;i++){
            // 对1做位移运算并将第i位进行与运算便可以得出第i位是否为1
            if ((n&(1<<i))!=0){
                res++;
            }
        }
        return res;
    }

方法二：

使用位运算加速遍历过程

有公式n&(n-1)可以将n最右侧的1置换为0，原理在于n与n-1只相差1，

必然有2位是不一致的，且这2位都是最右侧的1.

时间O(logn)（最坏情况下所有位都是1，则循环次数为该二进制数的长度，n=2^i+2^i-1+...+2^0，i的值为logn），空间O(1)

public int hammingWeight(int n) {
        int res=0;
        while(n!=0){
            // 不停的将n的最右侧的1置换为0，最终将全部为0
            n=n&(n-1);
            res++;
        }
        return res;
    }

方法三：

JDK教做人系列：Integer.bitCount（汉明重量）

时间O(1)，空间O(1)

简述下该答案的思路大致为：

（1）将32位整数划分为C1,C2,C3,C4四个部分

（2）分别计算出D1,D2,D,3,C4（上文4个部分分别对应的1的个数）

（3）利用位移计算D1+D2+D3+D4的到最终结果

可以参考下这里的详细解释

https://blog.csdn.net/qq_27007509/article/details/112246576

public int hammingWeight(int n) {
        // 计算没2位有多少个1
        n = (n & 0x55555555) + ((n >>> 1) & 0x55555555);
        // 计算没4位有多少个1
        n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
        // 计算没8位有多少个1
        n = (n & 0x0f0f0f0f) + ((n >>> 4) & 0x0f0f0f0f);
        // 右移1位并于原值相加，计算出计算D4+D3
        n = n + (n >>> 8);
        // 右移2位并与原址，计算出D4+D3+(D2+D1)
        n = n + (n >>> 16);
        // 计算出D4的值并返回
        return n & 0x3f;
    }