[Algorithms] Topological Sort

Topological sort is an important application of DFS in directed acyclic graphs (DAG). For each edge (u, v) from node u to node v in the graph, u must appear before v in the topological sort.

Topological sort has many interesting applications. One of them is job scheduling, in which you are assigned many jobs, each of the job has some prerequisite jobs, that means some jobs must be finished before you can move on to a particular job. If we express this dependency using a DAG (each job is represented as a node; if job u must be finished before job v, there is a directed edge from node u to node v), the topological sort of the graph will be a feasible schedule for the jobs.

The implementation of topogical sort is based on the previous graph representation and the DFS algorithms in this passage. I also implement a function read_digraph to input a directed graph manually. It is basically the same to the function read_graph in the above link. You may refer to it for the formatting style of the graph and more information.

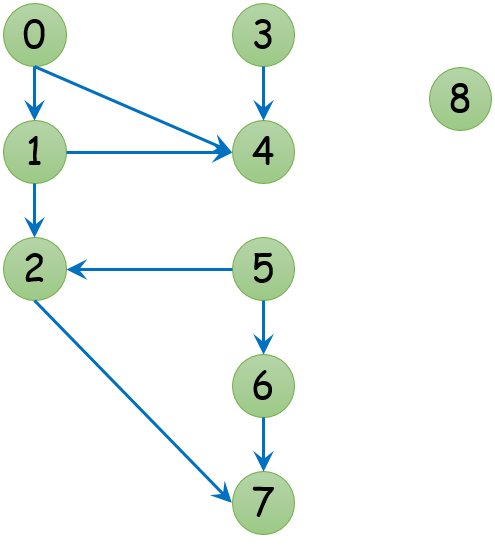
The following graph is used to test the code.

The code is as follows.

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_set>

using namespace std;

struct GraphNode {
    int label;
    vector<GraphNode*> neighbors;
    GraphNode(int _label) : label(_label) {}
};

vector<GraphNode*> read_digraph(void) {
    int num_nodes, num_edges;
    scanf("%d %d", &num_nodes, &num_edges);
    vector<GraphNode*> graph(num_nodes);
    for (int i = 0; i < num_nodes; i++)
        graph[i] = new GraphNode(i);
    int node, neigh;
    for (int i = 0; i < num_edges; i++) {
        scanf("%d %d", &node, &neigh);
        graph[node] -> neighbors.push_back(graph[neigh]);
    }
    return graph;
}

void topological(vector<GraphNode*>& graph, GraphNode* node, 
                 unordered_set<GraphNode*>& visited, vector<GraphNode*>& nodes) {
    visited.insert(node);
    for (GraphNode* neigh : node -> neighbors)
        if (visited.find(neigh) == visited.end())
            topological(graph, neigh, visited, nodes);
    nodes.push_back(node);
}

vector<GraphNode*> topological_sort(vector<GraphNode*>& graph) {
    vector<GraphNode*> nodes;
    unordered_set<GraphNode*> visited;
    for (GraphNode* node : graph)
        if (visited.find(node) == visited.end())
            topological(graph, node, visited, nodes);
    reverse(nodes.begin(), nodes.end());
    return nodes;
}

void graph_test(void) {
    vector<GraphNode*> graph = read_digraph();
    // Topological Sort
    printf("Topological Sort:
");
    vector<GraphNode*> topo_sort = topological_sort(graph);
    for (GraphNode* node : topo_sort)
        printf("%d ", node -> label);
    printf("
");
}

int main(void) {
    graph_test();
    system("pause");
    return 0;
}

The above graph is input as as follows:

9 9
0 1
1 4
1 2
2 7
3 4
0 4
5 2
5 6
6 7

The output is as follows:

Topological Sort:
8 5 6 3 0 1 2 7 4

Now if you reorder the nodes of the graph in the order of the topological sort, all the edges will be pointing from left to right, as shown in the graph below.