洛谷P3811 乘法逆元

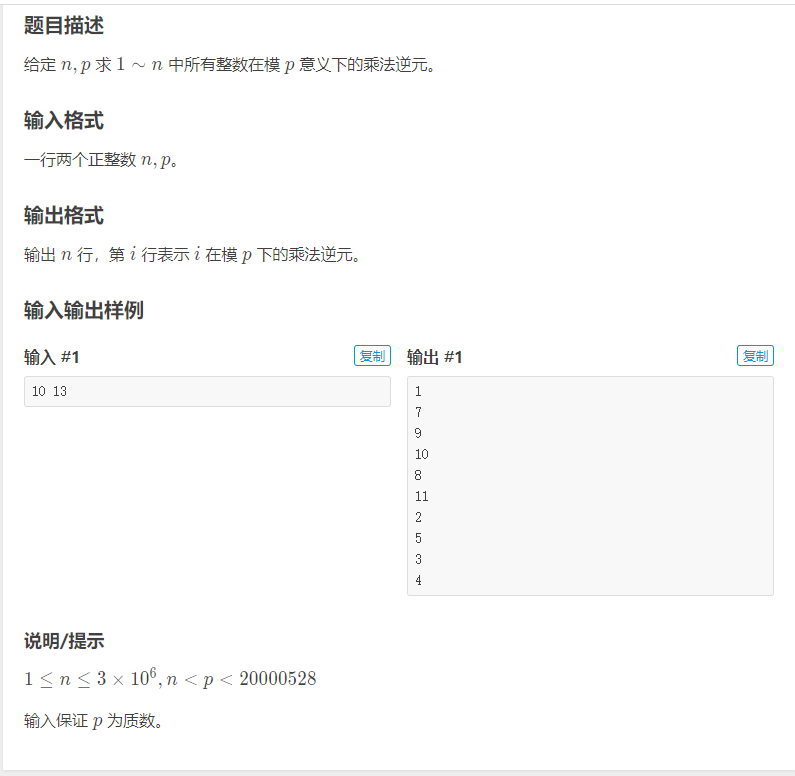
这道题的求逆元需可以用扩展欧几里得来求，这里用一种新方法，使用线性递推来求解

首先，假设有一个数 p ，有：p = k * i + r ，那么，k=p / i，r = p % i

那么就有 k * i + r ≡ 0 （mod p）

同时乘上 i^-1 * r^-1 ，就有 k * r^-1 + i^-1 ≡ 0 （mod p）

移项，就有 i^-1 ≡ - k * r^-1 （mod p)

将 k=p / i，r = p % i 代入，得： i^-1 ≡ -（ p / i ）*（ p % i ）^-1 （mod p）

那么，p % i 明显是要小于 i 的 ，那么我们就可以利用 （p % i）^-1 ，来求得 i^-1

但是，我们还需要保证 i^-1 是一个正数，那么就需要再加上一个 p , 这并不影响我们的结果，因为 a + b ≡ a （mod b）

那么，我们的最终结果就是：inv[i] = p - ( p / i ) * inv[p%i] % p

最后，只要将 inv[0] ，inv[1] 分别赋值为 0，1，就可以推出全部的逆元结果

见代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<math.h>
using namespace std;

long long a[30000001]; 
int n,p;

/*inline int read(){//可以用快读，不过scanf已经够了
    int f=1,x=0;char ch;
    do{ch=getchar();if(ch=='-')f=-1;}while(ch<'0'||ch>'9');
    do{x=x*10+ch-'0';ch=getchar();}while(ch>='0'&&ch<='9');
    return f*x;
}*/

int main(void)
{
    scanf("%d%d",&n,&p);
    
    a[1]=1;
    
    cout<<1<<endl;
    
    for(int i=2;i<=n;i++)
    {
        a[i]=1ll*(p-p/i)*a[p%i]%p;//递推公式套用
        
        printf("%d
",a[i]);
    }
    
    return 0;
}