洛谷 P1030 求先序排列

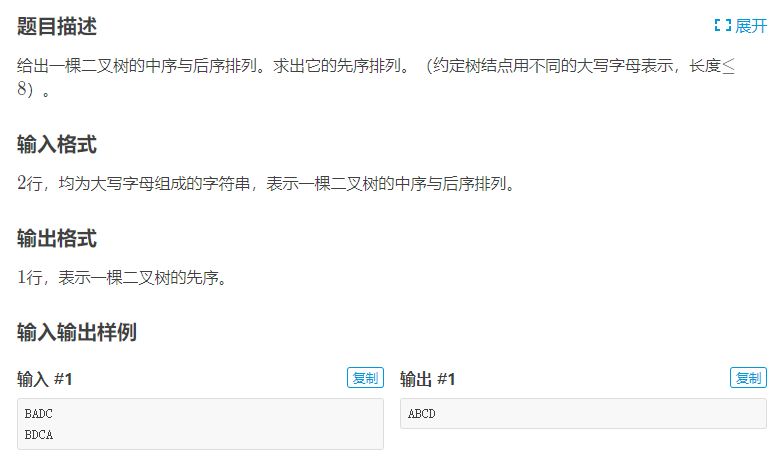
这道题中，有几个可以确定的信息

1.后序排列的最后一个元素必然是这个树的主根节点

2.我们在输出的时候，可以只需要输出访问的父节点即可，那么就只需要把一个树不断地分为两个子树，然后找到他们的父节点，不断地递归输出

那么，我们可以在中序遍历找到父节点之后，计算出他的左子树和右子树的节点数量。

然后，由于我们对结点的访问一定是先访问一颗子树，在访问另一颗，所以在我们的原后序遍历串右边界中减掉右子树节点个数再减一即为新的左子树右边界，在原后序遍

历串左边界加上左子树节点个数即为新的右子树左边界；

代码

#include<iostream>

#include<cstdio>

#include<algorithm>
#include<cstring>
#include<math.h>
using namespace std;

char s1[1000];
char s2[1000];
int len;

int find(char ch)
{
    for(int i=0;i<len;i++)
    {
        if(s1[i]==ch)
        {
            return i;
        }
    }
}

void dfs(int l1,int r1,int l2,int r2)//l1为左子树起点，r1为右子树起点，l2为左子树边界，r2为右子树边界
{
    int m=find(s2[r2]);
    
    cout<<s2[r2];
    
    if(m>l1)//有左子树 dfs(l1,m-1,l2,r2-r1+m-1);//r1-m为右子树节点数
    if(m<r1)//有右子树 dfs(m+1,r1,l2+m-l1,r2-1);//m-l1为左子树节点数
}

int main(void)
{
    cin>>s1;
    cin>>s2;
    
    len=strlen(s1);
    
    dfs(0,len-1,0,len-1);
    
    return 0;
}