题目:
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
- You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
- After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
prices = [1, 2, 3, 0, 2] maxProfit = 3 transactions = [buy, sell, cooldown, buy, sell]
提示:
这道题可以用动态规划的思路解决。但是一开始想的时候总是抽象不出状态转移方程来,之后看到了一种用状态机的思路,觉得很清晰,特此拿来分享,先看如下状态转移图:
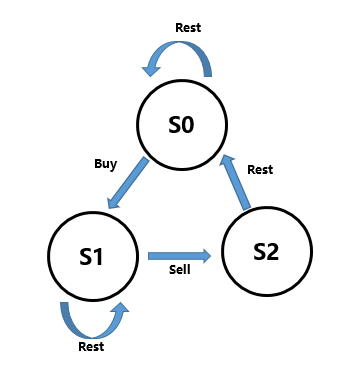
这里我们把状态分成了三个,根据每个状态的指向,我们可以得出下面的状态转移方程:
- s0[i] = max(s0[i-1], s2[i-1])
- s1[i] = max(s1[i-1], s0[i-1] - price[i])
- s2[i] = s1[i-1] + price[i]
这样就清晰了很多。
代码:
1 class Solution { 2 public: 3 int maxProfit(vector<int>& prices){ 4 if (prices.size() <= 1) return 0; 5 vector<int> s0(prices.size(), 0); 6 vector<int> s1(prices.size(), 0); 7 vector<int> s2(prices.size(), 0); 8 s1[0] = -prices[0]; 9 s0[0] = 0; 10 s2[0] = INT_MIN; 11 for (int i = 1; i < prices.size(); i++) { 12 s0[i] = max(s0[i - 1], s2[i - 1]); 13 s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]); 14 s2[i] = s1[i - 1] + prices[i]; 15 } 16 return max(s0[prices.size() - 1], s2[prices.size() - 1]); 17 } 18 };