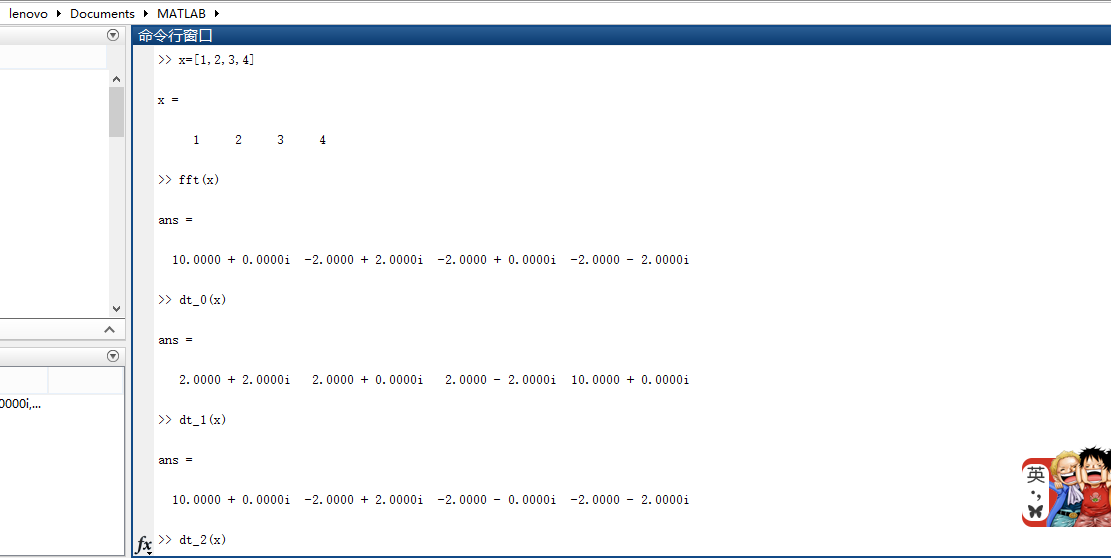
%用二重循环实现DFT: function xk=dt_0(xn); %define a function N=length(xn); %caculate the length of the variable WN=exp(-j.*2.*pi./N); xk=zeros(1,N); %define a non-zero 一维矩阵 sum=zeros(1,N); %define a non-zero 一维矩阵 for k=1:N %二重循环实现离散傅里叶变换DFT for n=1:N sum(n)=xn(n).*WN.^(k.*n); xk(k)=xk(k)+sum(n); end end end %用一重循环和内积实现DFT: function xk=dt_1(xn); N=length(xn); WN=exp(-j.*2.*pi./N); xk=zeros(1,N); n=[0:N-1]; for k=0:1:N-1; xk(k+1)=xn*WN.^(k.*n'); %此处下标一定得从1开始,因为matlab的下标是从1开始的 end end %不用循环,仅有内积相乘实现DFT: function xk=dt_2(xn); N=length(xn); WN=exp(-j*2*pi/N); n=0:1:N-1; %定义一个一维矩阵,即行向量,从0到N-1 k=0:1:N-1; nk=k'*n; %行向量k变换为列向量 乘上 行向量n ,得到一个N x N的矩阵 WNnk=WN.^(nk); %做幂运算后的参数仍为一个 N x N的系数矩阵 xk=xn*WNnk; %行向量 乘以 N x N的系数矩阵 即为DFT变换后的矩阵 end
以下是输入一个行向量xn=[1,2,3,4],MATLAB中用以上三种方法进行DFT的结果如下图所示: