强推啊。
永远无法知道概率论的利用会如此之大。
摘要:
不同的文字系统在记录信息上的能力是等价的。
文字只是信息的载体,而非信息本身。
机器翻译和语言识别,全都靠的是数学,更准确的是统计。
20世纪60年代,基于乔姆斯基形式语言的编译器技术得到了很大的发展,计算机高级程序语言都可以概括成上下文无关的文法,这是一个在算法上可以在多项式时间内解决的问题。
上下文无关算法可以想看计算理论导论...
基于统计的语言处理的核心模型是通信系统加隐含马尔可夫模型。
统计语言模型:马尔可夫假设:(二元模型)
假设任意一个词出现的概率只同它前面的词有关。
因为有了大量机读文本,也就是专业人士讲的语料库,只要数一数Wi-1,Wi这对词在统计的文本中前后相邻出现了多少次,以及Wi-1本身在同样的文本中出现了多少次,然后用两个数分别除以语料库的大小,即可得到这些词或者二元组的相对频度。 根据大数定理,只要统计量足够,相对频度就等于概率。 如上是统计语言模型的理论。用来解决复杂的语音识别、机器翻译等问题。
假定文本中的每个词Wi和前面的N-1个词有关,而与更前面的词无关。这样当前词wi的概率只取决于前面的N-1个词 P(Wi-N+1,Wi-N+2,...,Wi-1).
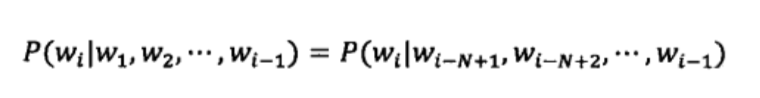
这种假设被称为N-1阶马尔可夫假设,对应的语言模型称为N元模型。N=1的一元模型实际上是一个上下文无关模型,也就是假定当前词出现的概率与前面的词无关。而在实际应用中最多的是N=3.
空间复杂度为|v|的N-1次幂。|v|是一种语言词典的词汇量。
使用语言模型需要知道模型中所有的条件概率,称之为模型的参数。
如果用直接的比值计算概率,大部分条件概率依然是零,这种模型我们称之为不平滑,在实际应用中,统计语言模型的零概率问题是无法回避的,必须解决。
训练统计语言模型的艺术就在于解决好统计样本不足时的概率估计问题。
古德提出在统计中相信可靠的统计数据,面对不可信的统计数据打折扣的一种概率估计方法,同时将折扣出来的那一小部分概率给予未看见的事件。有一个重新估算概率的公式。称为 古德-图灵估计。原理为:对于没有看见的事件,我们不能认为它发生的概率就是0,因此我们从概率的总量中,分配一个很小的比例给予这些没有看见的事件。这样一来,看见的那些事件的概率总和就要小于1了。因此,需要将所有看见的事件概率调小一点,至于小多少,要根据“越是不可信的统计折扣越多”的方法进行。
隐含马尔可夫模型最初应用于通信领域,继而推广到语音和语言处理中,成为连接自然语言处理和通信的桥梁。同时,隐含马尔可夫模型也是机器学习主要工具之一。它需要一个训练算法(鲍姆-韦尔奇算法)和使用时的编码算法(维特比算法)。
信息的度量,信息熵,越小,表明数据越纯。
信息量就等于不确定性的多少。
如果没有信息,任何公式或者数字的游戏都无法排出不确定性。
几乎所有的自然语言处理、信息与信号处理的应用都是一个消除不确定性的过程。
熵描述一个元素的不确定性大小。
搜索引擎的原理很简单,建立一个搜索引擎大致需要做这样几件事:自动下载尽可能多的网页;建立快速有效的索引;根据相关性对网页进行公平准确的排序。
布尔代数(0、1/ true、false)对于数学的意义是将我们对世界的认识从连续状态扩展到离散状态。
现代物理的研究成果表明,我们的世界实实在在是量子化的而不是连续的。我们的宇宙的基本粒子数目是有限的,而且远比古高尔(10的100次幂)要小得多。
搜索引擎会自动把用户的查询语句转换成布尔运算的算式。
计算机做布尔运算时非常快的,最便宜的微机都可以在一个指令周期进行32位布尔运算,一秒钟进行数十亿次以上。
互联网虽然很复杂,但是说穿了其实就是一张大图而已,可以把每一个网页当作一个节点,把那些超链接当作连接网页的弧。可以从任何一个网页出发,用图的遍历算法,自动地访问到每一个网页并把他们存起来。完成这个功能的程序叫做网络爬虫。在网络爬虫中,使用一个成为哈希表的列表而不是一个记事本记录网页是否下载过的信息。
网络爬虫在工程上的实现?
1. BFS还是 DFS?
网络爬虫对网页遍历的次序不是简单的BFS或者DFS,而是有一个相对复杂的下载优先级排序的方法。管理这个优先级排序的子系统一般称为调度系统。由它来决定当一个网页下载完成后,接下来下载哪一个。当然在调度系统里需要存储那些已经发现但是尚未下载的网页url,它们一般存在一个优先级队列里。
2.页面的分析和url的提取。
当一个网页下载完成后,需要从这个网页中提取其中的URL,把它们加入到下载的队列中。早期互联网的网页是由html实现的,提取url不难。现在使用一些脚本语言如javascript生成的。打开网页的源代码,url不是直接可见的文本,而是运行这一段脚本后才能得到的结果。因此,网络爬虫的页面分析就变得复杂很多,要模拟浏览器运行一个网页,才能得到里面隐含的url。因此,需要做浏览器内核的工程师来写网络爬虫中的解析程序,可惜出色的浏览器内核工程师在全世界数量并不多。因此,若发现一些网页明明存在,但搜索引擎就是没有收录,一个可能的原因就是网络爬虫中的解析程序没能成功解析网页中不规范的脚本程序。
3.记录哪些网页下载过-url表
为了防止一个网页被下载多次,需要在一个哈希表中记录哪些网页已经下载过。采用哈希表的好处是,判断一个网页的url是否在表中,平均只需要一次或者略多的查找。维护一张哈希表不现实,太大,其次,由于每个下载服务器在开始下载前和完成下载后都要访问和维护这张表,以免不同的服务器做重复的工作,这个存储哈希表的服务器的通信就成了整个爬虫系统的瓶颈。
解决方案明确每台下载服务器的分工,判断url是否下载--》批处理。
网页排名。
PageRank算法,在互联网上,如果一个网页被很多其他网页所链接,说明它受到普遍的承认和信赖,那么它的排名就高,这就是pagerank的核心思想。
网页排名的高明之处在于它把整个互联网当作一个整体来对待。这无意识中符合了系统论的观点。相比之下,以前的信息检索大多把每一个网页当作独立的个体对待,大部分人当初只注意了网页内容和查询语句的相关性,忽略了网页之间的关系。
pagerank算法二维矩阵,Amn表示第m个网页指向第n个网页的链接数。迭代进行收敛,算出排名值,值越大,越先显示。由于网页之间链接的数量相比互联网的规模非常稀疏,因此计算网页的网页排名也需要对0概率或者小概率事件进行平滑处理。网页的排名是个一维向量,对它的平滑处理只能利用一个小的常数。
网页排名的计算主要是矩阵相乘,这种计算很容易分解成多个小任务,在多台计算机上并行。
确定网页和查询的相关性。TF-IDF(term frequency/inverse document frequency)
如果一个关键词只在很少的网页中出现,通过它就容易锁定搜索目标,它的权重也就应该大。分之,如果一个词在大量网页中出现,看到它仍然不很清楚要找什么内容,因此它的权重就应该小.
所谓IDF的概念就是一个特定条件下关键词的概率分布的交叉熵。
地图和本地搜索的最基本技术--有限状态机和动态规划
地址的识别和分析,地址的文法是上下文有关文法中相对简单的一种,因此有许多识别和分析的文法,但最有效的是有限状态机。关键要解决两个问题,即通过一些有效的地址建立状态机,以及给定一个有限状态机后,地址字串的匹配算法。担当用户输入的地址不太标准则需要模糊匹配,为了实现这个目的,基于概率的有限状态机,这种基于概率的有限状态机和离散的马尔可夫链基本上等效。
全球导航的关键算法是计算机科学图论中的动态规划的算法。加权图。最短路径。可以将一个寻找全程最短路线的问题,分解成一个个寻找局部最短路线的小问题,这便是动态规划的原理。
有限状态机的应用远不止地址的识别,今天的语音识别解码器基本上是基于有限状态机的原理。另外,它在编译原理、数字电路设计上有着非常重要的应用。
DFA定义,5元组:起始状态、有限状态集合、输入符号的集合、映射函数、终止状态。
DFA主要是指从一个状态到另一个状态是确定的。详情可以参考计算理论导论。
有限状态传感器的特殊性在于,有限状态机中的每个状态由输入和输出符号定义。
有限状态机和动态规划的应用非常广泛,远远不止识别地址、导航等地图服务相关领域。它们在语音识别、拼写和语法纠错、拼音输入法、工业控制和生物的序列分析等领域都有着极其重要的应用。
新闻的分类很大程度上依靠余弦定理。新闻由计算机整理、分类和聚合各个新闻网站的内容,一切都是自动生成的,这里面的关键技术就是新闻的自动分类。
计算机本质上只能做快速计算。为了让计算机能够算新闻,就要求我们首先把文字的新闻变成可以计算的一组数字,然后再设计一个算法来算出任意两篇新闻的相似性。首先,怎样找一组数字或者说一个向量来描述一篇新闻,新闻是传递信息的,而词是信息的载体,新闻的信息和词的语义是联系在一起的。计算TF-IDF。然后用这个值组成特征向量来描述新闻。每一篇新闻都可以对应这样一个特征向量,向量中每一个维度的大小代表每个词对这篇新闻主题的贡献。当新闻从文字变成了数字后,计算机就有可能算一算新闻之间是否相似了。
定性地认识到两篇新闻的主题是否接近,取决于它们的特征向量长得像不像。当然,我们还需要定量地衡量两个特征向量之间的相似性。
向量的方向却有很大的意义。如果两个向量的方向一致,说明相应的新闻用词的比例基本一致。因此,可以通过计算两个向量的夹角来判断对应的新闻主题的接近程度。而要计算两个向量的夹角,就要用到余弦定理了。
在自然语言处理中,最常见的两个分类问题分别是,将文本按主题归类和将词汇表中的字词按意思归类。这两个分类问题都可以通过矩阵运算解决。
新闻分类乃至各种分类其实是一个聚类问题,关键是计算两篇新闻的相似程度。为了完成这个过程,我们要将新闻变成代表它们内容的实词,然后再变成一组数,具体说是向量,最后求这两个向量的夹角。当这两个向量的夹角很小时,新闻就相关,当他们垂直或者说正交时,新闻则无关。但是因为要对所有新闻做两两计算,而且要进行多次迭代,因此耗时特别长,尤其是当新闻的数量很大,同时词表也很大的时候,希望有一个方法,一次就能把所有新闻相关性计算出来,这个一步到位的办法就是利用矩阵运算的奇异值分解(Singular Value Decomposition,SVD)。
SVD: 需要一个大矩阵来描述文章和词的关联性。在这个矩阵中,每一行对应一篇文章,每一列对应一个词,如果有n个词,m篇文章,那么就是一个m*n矩阵。第i行、第j列第元素是字典中第j个词在第i篇文章中出现的加权词频。奇异词分解,就是把上面这样一个大矩阵,分解成三个小矩阵相乘。三个矩阵有非常清晰的物理含义。第一个矩阵是对词进行分类的一个结果。它的每一行表示一个词,每一列表示一个语义相近的词类,或者简称为语义类。这一行的每个非零元素表示这个词在每个语义类中的重要性或者说是相关性,数值越大越相关。最后一个矩阵时对文本的分类结果。它的每一列对应一个文本,每一行对应一个主题。这一列中每个元素表示在这篇文本在不同主题中的相关性。中间的矩阵则表示词的类和文章的类之间的相关性。
如何利用计算机进行奇异值分解....
任何一段信息,都可以对应一个不太长的随机数,作为区别它和其他信息的指纹。只要算法设计的好,任何两段信息的指纹都难以重复。信息指纹在加密、信息压缩和处理中有着广泛的应用。
假设能够找到一个函数,将5000亿个网址随机地映射到128位二进制,也就是16个字节的整数空间,这样,每个网址就只需要占用16个字节而不是原来的100个。这个16字节的随机数,就称作该网址的信息指纹。网络爬虫在下载网页时,它将访问过的网页地址都变成一个个信息指纹,存到哈希表中,每当遇到一个新网址,计算机就计算出它的指纹,然后比较该指纹是否已经在哈希表中,来决定是否下载这个网页。
网址的信息指纹的计算方法一般分为2步。首先,将这个字符串看成是一个特殊的、长度很长的整数。接下来就需要一个产生信息指纹的关键算法:伪随机数产生器算法,通过它将任意很长的整数转换成特定长度的伪随机数,这种是将一个数的平方掐头去尾,去中间的几位数,但是很有可能重复。现在常用的梅森旋转算法要好得多。
信息指纹的用途远不止网址的消重,孪生兄弟是密码。信息指纹的一个特征是其不可逆性,也就是说,无法根据信息指纹推出原有信息。这种性质,正是网络加密传输所需要的。
判断集合是否相同。最简单的笨方法是对这个集合中的元素一一作比较,时间复杂度是N的平方。稍微好一点点是将两个集合的元素分别排序然后顺序比较,这样时间复杂度是NlogN。处于同一个水平的方法是将第一个集合放在一张哈希表中,然后把第二个集合的元素一一和哈希表中的元素作对比。时间复杂度是N,但是额外使用了N的空间,代码复杂,不完美。完美的方法是计算这两个集合的指纹,然后直接进行比较。时间复杂度是N,不需要额外的空间。
比如在网页搜索中,判断两个网页是否是重复的。如果把两个网页的正文从头比到尾,计算时间太长,也没有必要。我们只需对每个网页挑出几个词,这些词构成网页的特征词集合。然后计算和比较这些特征集合的信息指纹即可。只需找出每个网页中IDF最大的几个词,并且计算出他们的信息指纹即可。如果两个网页这么计算出来的信息指纹相同,它们基本上是相同的网页。为了允许有一定的容错能力,google里采用了一种特定的信息指纹--相似哈希。
视频的匹配有两个核心技术,关键帧的提取和特征的提取。
信息指纹重复的可能性,很小。
信息指纹可以理解为将一段信息随机地映射到一个多维二进制空间中的一个点。只要这个随机函数做得好,那么不同信息对应的这些点不会重合,因此这些二进制的数字就成了原来信息所具有的独一无二的指纹。
当密码之间分布均匀并且统计独立时,提供的信息最少。
公钥、私钥。
公开秘钥方法保证产生的秘文是统计独立而分布均匀的。也就是说,不论给出多少份明文和对应的密文,也无法根据已知的明文和密文的对应来破译下一份密文。要破解公开秘钥的加密方式,至今的研究结果表明最好的办法还是对大数N进行因数分解。
自从有了搜索引擎,就有了针对搜索引擎网页排名的作弊。早期最常见的作弊方式是重复关键词。
搜索引擎作弊从本质上看就如同对搜索排序的信息加入噪音,因此反作弊的第一条是要增强排序算法的抗噪声能力,其次是像在信号处理中去噪音那样,还原原来真实的排名。信号加入噪音相当于卷积的过程,去噪相当于解卷积的过程。从广义上讲,只要噪音不是完全随机并且前后有相关性,就可以检测到并且消除。事实上,完全随机不相关的高斯白噪音是很难消除的。
具体的反作弊做法是,针对和商业相关的搜索,采用一套抗干扰强的搜索算法,这就如同在高噪音环境下采用抗干扰的麦克风一样。而对信息类的搜索,采用敏感的算法,就如同在安静环境下采用敏感的麦克风,对轻微的声音也能有很好的效果。那些卖链接的网站(作弊者发现一个网页被引用的链接越多,排名就可能越靠前),都有大量的出链,而这些出链的特点和不作弊网站的出链特点大不相同。每一个网站到其他网站到出链数目可以作为一个向量,它是这个网站固有的特征。既然是向量,我们就可以计算余弦距离。我们发现,有些网站到出链向量之间的余弦距离几乎为1,一般来讲这些网站通常是一个人建的,用于卖链接,改进pagerank算法,使得买来的链接不起作用。
在网络搜索的研发中,在前面提到的单文本词频/逆文本频率指数(TF-IDF)和网页排名可以看作是网络搜索中的椭圆模型。
最大熵模型:不要把所有的鸡蛋放在同一个篮子里。相当于行星运动的椭圆模型。要保留全部的不确定性,将风险降到最小。
最大熵原理指出,需要对一个随机事件的概率分布进行预测时,我们的预测应当满足全部已知的条件,而对未知的情况下不要做任何主观假设。在这种情况下,概率分布最均匀,预测的风险最小。因为这时概率分布的信息熵最大,所以人们称这种模型叫最大熵模型。因为当我们遇到不确定性时,就要保留各种可能性。
对任何一组不自相矛盾的信息,这个最大熵模型不仅存在,而且是唯一的。此外,它们都有同一个非常简单的形式--指数函数。很多复杂的问题都可以采用最大熵模型,包括句法分析、语言模型和机器翻译。
最大熵模型可以将各种信息整合到一个统一到模型中。它有很多良好的特性:从形式上看,它非常简单,非常优美;从效果上看,它是唯一一种可以满足各个信息源的限制条件,同时又能保证平滑特性。
输入法输入汉字的快慢取决于对汉字编码的平均长度,通俗的讲,就是击键次数乘以寻找这个键所需要的时间。
将汉字输入到计算机中,本质上是一个将我们人为约定的信息记录编码--汉字,转换成计算机约定的编码,国际码或者UTF-8的信息转换过程。对汉字的编码分为两部分:对拼音的编码和消除歧义性的编码。
语言和文字作为通信的编码手段,一个重要目的是帮助思维和记忆。如果一个输入法中断了人们的思维过程,就和人的自然行为不相符合。
香农第一定理指出,对于一个信息,任何编码的长度都不小于它的信息熵。
拼音转汉字的算法和在导航中寻找最短路径的算法相同,都是动态规划。
布隆过滤器
在日常生活中,包括设计计算机软件时,经常要判断一个元素是否在一个集合中。比如,在字处理软件中,需要检查一个英语单词是否拼写正确;在网路爬虫里,一个网址是否已访问过。最直接的方法就是将集合中全部元素存在计算机中,遇到一个新元素时,将它和集合中的元素直接比较即可。一般来讲,计算机中的集合是用哈希表来存储的。好处是快速准确,缺点是耗费存储空间。用哈希表实现的具体办法是将每一个email地址对应成一个8字节的信息指纹,然后将这些信息指纹存入哈希表,由于哈希表的存储效率一般只有50%。使用布隆过滤器的数学工具,只需要哈希表的1/8到1/4的大小就可以解决同样的问题。
布隆过滤器背后的数学原理在于两个完全随机的数字冲突的概率很小,因此,可以做很小的误识别率条件下,用很少的空间存储大量信息。常见的补救误识别的方法是再在建立一个小的白名单,存储那些可能被识别兀判断信息。
贝叶斯网络,加权网络图。假定在这个图中马尔可夫假设成立,即每一个状态只和与它直接相连的状态有关,而和它间接相连的状态没有直接关系,那么它就是贝叶斯网络。
马尔可夫链是贝叶斯网络的特例,而贝叶斯网络是马尔可夫链的推广。
使用贝叶斯网络必须先确定这个网络的拓扑结构,然后还要知道各个状态之间相关度概率。得到拓扑结构和这些参数的过程叫做结构训练和参数训练,统称训练。从理论上讲,它是一个NP完备问题,也就是说,对于现在的计算机是不可计算的。
贝叶斯网络在图像处理、文字处理、支持决策等方面有很多应用。在文字处理方面,语义相近的词之间的关系可以用一个贝叶斯网络来描述。