编译原理词法分析：从正则表达式到生成代码

引言

最近在学编译原理，一门理论与实践结合的课程，我把作业发到博客里，希望能与大家交流分享。

词法分析一章有一道比较复杂的作业题如下：

本题是一个编程问题，在本题目中，你将完整的实现Thompson算法、子集构造算法和Hopcroft算法。为了帮助你开始，请下载如下链接中的代码并根据代码运行时的提示将缺少的代码补充完整。（注意，我们给出了正则表达式和NFA的数据结构和Thompson算法的框架，其它的数据结构和算法需要你自行补充完整。）

代码链接：http://staff.ustc.edu.cn/~bjhua/mooc/thompson.rar

由于我写起C来就跟Cfront一样，我还是写C++吧。为了增加一点难度，我把原题的3步扩展为5步：构造正则表达式、Thompson构造法、子集构造算法、Hopcroft算法、生成C++代码。

虽然属于词法分析部分，这道题的目标是实现词法分析器生成器，已经有点语法分析的意味，不过上下文无关文法换成了正则表达式。

完整代码

构造正则表达式

设(Sigma)为所有可能字符构成的集合。正则表达式（Regular Expression/regex/RE）是一串定义搜索样式的字符，用于匹配由取自(Sigma)中的字符组成的字符串。RE的定义是递归的：

• 空串(varepsilon)是RE；

• (forall c in Sigma)，(c)是RE；

• 如果(M)和(N)都是RE，则以下都是RE：

  • (MN)，表示(M)后跟(N)；

  • (M|N)，表示(M)或(N)；

  • (M*)，表示(varepsilon)或若干个(M)，称为(M)的Kleene闭包；

这是最基本的RE，诸如[0-9]和e+之类都属于语法糖，我的实现中不涉及。

首先定义正则表达式类型：

class Regex
{
public:
    Regex();
    Regex(const Regex&) = delete;
    virtual ~Regex() = 0;
};

class Regexvarepsilon : public Regex
{
public:
    virtual ~Regexvarepsilon() override;
    Regexvarepsilon();
};

class RegexChar : public Regex
{
public:
    virtual ~RegexChar() override;
    RegexChar(char);
    char c;
};

class RegexConcat : public Regex
{
public:
    virtual ~RegexConcat() override;
    RegexConcat(Regex*, Regex*);
    Regex* re0;
    Regex* re1;
};

class RegexAlter : public Regex
{
public:
    virtual ~RegexAlter() override;
    RegexAlter(Regex*, Regex*);
    Regex* re0;
    Regex* re1;
};

class RegexClosure : public Regex
{
public:
    virtual ~RegexClosure() override;
    RegexClosure(Regex* re);
    Regex* re;
};

Regex::Regex() = default;

Regex::~Regex() = default;

Regexvarepsilon::~Regexvarepsilon() = default;

Regexvarepsilon::Regexvarepsilon() = default;

RegexChar::~RegexChar() = default;

RegexChar::RegexChar(char c)
    : c(c)
{
    ;
}

RegexConcat::~RegexConcat()
{
    delete re0;
    delete re1;
}

RegexConcat::RegexConcat(Regex* re0, Regex* re1)
    : re0(re0), re1(re1)
{
    ;
}

RegexAlter::~RegexAlter()
{
    delete re0;
    delete re1;
}

RegexAlter::RegexAlter(Regex* re0, Regex* re1)
    : re0(re0), re1(re1)
{

}

RegexClosure::~RegexClosure()
{
    delete re;
}

RegexClosure::RegexClosure(Regex* re)
    : re(re)
{
    ;
}

Regex和它的子类们把new的任务交给客户，析构函数负责delete。如果Regex要拷贝的话需要递归深拷贝，很容易实现，但我不需要，所以写= delete。

stringToRegex函数用于把字符串转换为Regex*，实现思路如下：

1. 如果输入是(...)但不是(...)...(...)样式的字符串，去掉两边的圆括号，因为它们没有用；

2. 如果|存在于最外层（即...(...|...)...不算），对|分割的每一个子RE递归调用该函数，然后用RegexAlter连接起来；

3. 否则，对于每一个带括号的子RE递归调用，对于字符直接构造RegexChar，把空格当做(varepsilon)（这两个是递归出口），都放到栈中（实现中用std::vector），遇到*时弹出栈顶，套上RegexClosure并放回。

static Regex* stringToRegex(std::string::const_iterator begin, decltype(begin) end)
{
    return stringToRegex(std::string{ begin, end });
}

Regex* stringToRegex(const std::string& string)
{
    auto begin = string.begin();
    auto end = string.end();
    while (1)
    {
        if (begin == end)
            return makeRegex<Regexvarepsilon>();
        if (*begin != '(')
            break;
        int level = 0;
        bool bk = false;
        for (auto iter = begin, e = end - 1; iter != e; ++iter)
            if (*iter == '(')
                ++level;
            else if (*iter == ')' && --level == 0)
                bk = true;
        if (bk)
            break;
        ++begin;
        --end;
    }
    std::vector<std::string::const_iterator> alts;
    int level = 0;
    for (auto iter = begin; iter != end; ++iter)
        switch (*iter)
        {
        case '(':
            ++level;
            break;
        case ')':
            --level;
            break;
        case '|':
            if (level == 0)
                alts.push_back(iter);
            break;
        }
    if (alts.empty())
    {
        std::vector<Regex*> cons;
        for (auto iter = begin; iter != end; ++iter)
        {
            switch (*iter)
            {
            case ' ':
                cons.push_back(makeRegex<Regexvarepsilon>());
                break;
            case '*':
            {
                auto back = cons.back();
                cons.pop_back();
                cons.push_back(makeRegex<RegexClosure>(back));
                break;
            }
            case '(':
            {
                int level = 0;
                auto begin = iter;
                for (; ; ++iter)
                    if (*iter == '(')
                        ++level;
                    else if (*iter == ')' && --level == 0)
                        break;
                cons.push_back(stringToRegex(begin, iter + 1));
                break;
            }
            default:
                cons.push_back(makeRegex<RegexChar>(*iter));
                break;
            }
        }
        auto regex = cons.front();
        for (auto iter = cons.begin() + 1; iter != cons.end(); ++iter)
            regex = makeRegex<RegexConcat>(regex, *iter);
        return regex;
    }
    else
    {
        auto size = alts.size();
        alts.push_back(end);
        auto regex = stringToRegex(begin, alts.front());
        for (decltype(size) i = 0; i != size; ++i)
            regex = makeRegex<RegexAlter>(regex, stringToRegex(alts[i] + 1, alts[i + 1]));
        return regex;
    }
}

以(a|b)(c|d)*为例，构造出的Regex树如图：

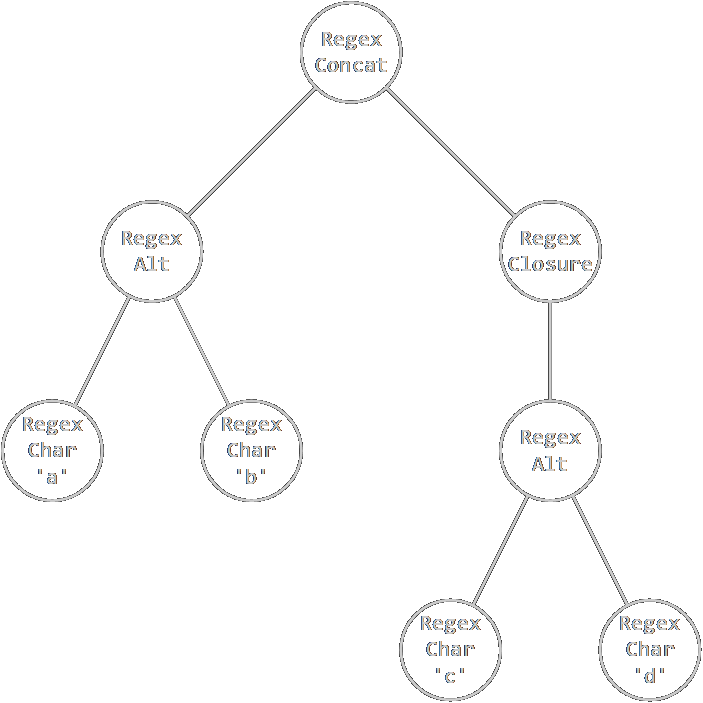
BTW，可否写个RE来匹配所有RE？

Thompson构造法

Thompson构造法可以把正则表达式转换为非确定性有限自动机（nondeterministic finite automaton，NFA），“非确定性”指的是状态和状态之间可以用(varepsilon)来转移。

首先给出Nfa的定义：

class NfaNode
{
public:
    std::vector<NfaNode*> eps;
    std::map<char, NfaNode*> map;
    bool accept = false;
};

class Nfa
{
public:
    explicit Nfa(const Regex*);
    Nfa(const Nfa&) = delete;
    Nfa& operator=(const Nfa&) = delete;
    Nfa(Nfa&&) noexcept;
    Nfa& operator=(Nfa&&) noexcept;
    ~Nfa();
    NfaNode* begin = nullptr;
    NfaNode* end = nullptr;
private:
    std::vector<NfaNode*> nodes;
    NfaNode* makeNode();
    Nfa makeSubNfa(const Regex*);
};

Nfa::Nfa(Nfa&&) noexcept = default;

Nfa& Nfa::operator=(Nfa&& other) noexcept
{
    begin = other.begin;
    end = other.end;
    nodes.swap(other.nodes);
    return *this;
}

Nfa::~Nfa()
{
    for (auto&& p : nodes)
        delete p;
}

NfaNode* Nfa::makeNode()
{
    auto ptr = new NfaNode;
    nodes.push_back(ptr);
    return ptr;
}

Nfa Nfa::makeSubNfa(const Regex* regex)
{
    auto temp = regexToNfa(regex);
    nodes.insert(nodes.end(), temp.nodes.begin(), temp.nodes.end());
    temp.nodes.clear();
    return temp;
}

NfaNode表示NFA中的状态：eps为该状态可以通过(varepsilon)转移到的状态的集合；map为(Sigma)中字符到对应目标状态的映射；accept指示该状态是否为接受状态。

Nfa表示NFA：用nodes保存由makeNode创建的Nfa指针，在析构函数中统一销毁；begin和end表示起始和接受状态。NFA是图，拷贝要复杂得多，由于不需要（其实是我懒），故= delete之。Nfa要作为参数传递，移动构造还是需要的。

C++新手小课堂：

问：std::vector中元素的迭代器和指针不是会失效吗？为什么可以让NfaNode保存NfaNode*呢？

答：因为std::vector的模板参数是NfaNode*而非NfaNode，NfaNode*是存储的值，不会失效。

RE是递归的，Thompson构造法亦是。为了方便递归，需要对产生的NFA作一些规约：

• NFA有唯一的起始状态；

• NFA有唯一的接收状态，该状态没有向其他状态的转移；

然后就可以递归地构造了：

• 空串(varepsilon)构造为：

  

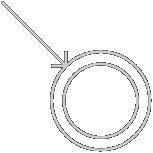
• 字符(c)构造为：

  

• (MN)构造为：

  

• (M|N)构造为：

  

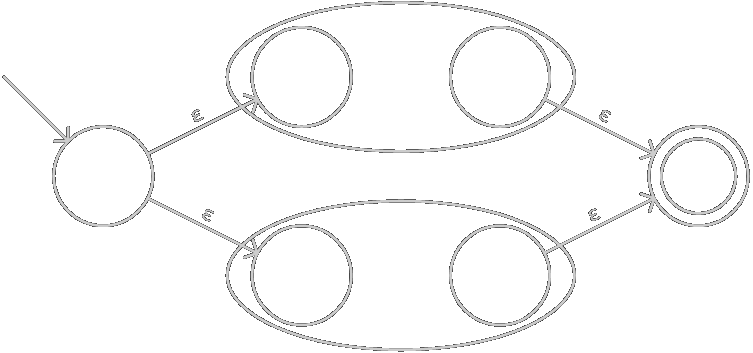
• (M*)构造为：

  

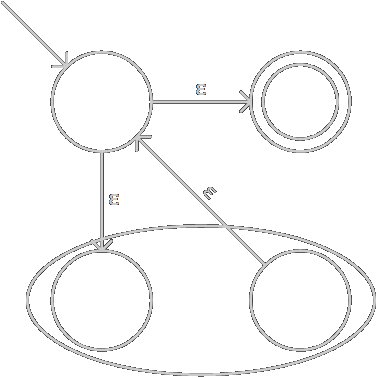
我对Thompson构造法的定义与标准的略有不同：我去掉了NFA起始状态不能作为转移目标状态的要求，于是对闭包的构造减少了一个节点；同时对连接的构造增加了一个节点，不过这也有以上数据结构不方便删除一个节点的考虑。

Nfa::Nfa(const Regex* regex)
{
    if (dynamic_cast<const Regexvarepsilon*>(regex))
    {
        begin = makeNode();
        end = begin;
        end->accept = true;
    }
    else if (dynamic_cast<const RegexChar*>(regex))
    {
        auto r = static_cast<const RegexChar*>(regex);
        begin = makeNode();
        end = makeNode();
        end->accept = true;
        begin->map[r->c] = end;
    }
    else if (dynamic_cast<const RegexConcat*>(regex))
    {
        auto r = static_cast<const RegexConcat*>(regex);
        begin = makeNode();
        auto nfa0 = makeSubNfa(r->re0);
        auto nfa1 = makeSubNfa(r->re1);
        begin->eps.push_back(nfa0.begin);
        nfa0.end->eps.push_back(nfa1.begin);
        nfa0.end->accept = false;
        end = nfa1.end;
    }
    else if (dynamic_cast<const RegexAlter*>(regex))
    {
        auto r = static_cast<const RegexAlter*>(regex);
        begin = makeNode();
        end = makeNode();
        auto nfa0 = makeSubNfa(r->re0);
        auto nfa1 = makeSubNfa(r->re1);
        begin->eps.push_back(nfa0.begin);
        nfa0.end->eps.push_back(end);
        nfa0.end->accept = false;
        begin->eps.push_back(nfa1.begin);
        nfa1.end->eps.push_back(end);
        nfa1.end->accept = false;
        end->accept = true;
    }
    else if (dynamic_cast<const RegexClosure*>(regex))
    {
        auto r = static_cast<const RegexClosure*>(regex);
        begin = makeNode();
        end = makeNode();
        auto nfa = makeSubNfa(r->re);
        begin->eps.push_back(end);
        begin->eps.push_back(nfa.begin);
        nfa.end->accept = false;
        nfa.end->eps.push_back(begin);
        end->accept = true;
    }
}

仍以(a|b)(c|d)*为例，构造出的NFA如图：

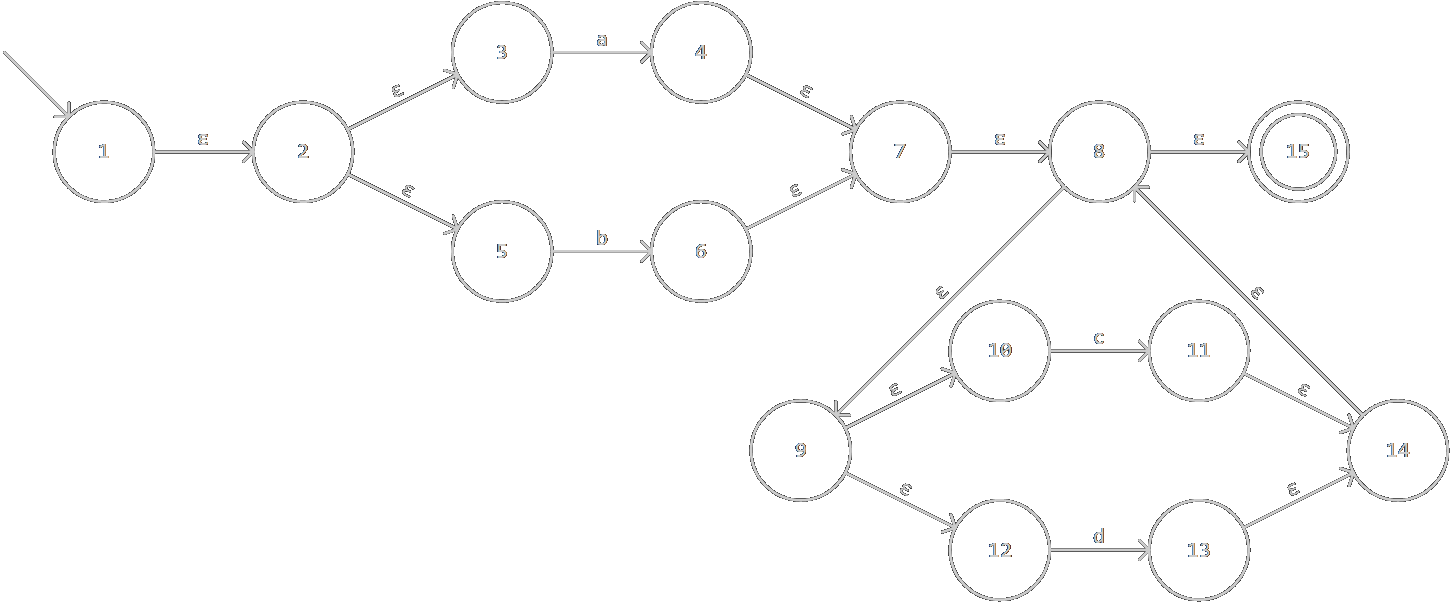
子集构造算法

NFA是不确定的，尽管有算法可以用NFA来匹配字符串，但是DFA（deterministic finite automaton，确定性有限自动机）更加简单、直观，因为它没有(varepsilon)转移，并且每个状态每个字符有唯一的转移目标（用Thompson构造法构造出的NFA也符合这一点）。

子集构造算法可以从NFA构造DFA。先给出DFA的定义：

class SimpDfa;

class DfaNode
{
public:
    std::map<char, std::size_t> map;
    bool accept = false;
};

class Dfa
{
public:
    Dfa();
    Dfa(const Dfa&) = delete;
    Dfa& operator=(const Dfa&) = delete;
    Dfa(Dfa&&) noexcept;
    Dfa& operator=(Dfa&&) noexcept;
    ~Dfa();
    DfaNode* getNode(std::size_t);
private:
    std::vector<DfaNode*> nodes;
    using SubsetMap = std::map<std::set<NfaNode*>, std::size_t>;
    SubsetMap subsetMap;
    std::pair<SubsetMap::iterator, bool> makeNode(const std::set<NfaNode*>&, bool);
    friend Dfa nfaToDfa(const Nfa& nfa);
    friend SimpDfa simplifyDfa(const Dfa& dfa);
};

Dfa::Dfa() = default;

Dfa::Dfa(Dfa&& other) noexcept
    : nodes(std::move(other.nodes))
{
    ;
}

Dfa& Dfa::operator=(Dfa&& other) noexcept
{
    nodes.swap(other.nodes);
    return *this;
}

Dfa::~Dfa()
{
    for (auto&& p : nodes)
        delete p;
}

DfaNode* Dfa::getNode(std::size_t index)
{
    return nodes[index];
}

这回DfaNode不再维护DfaNode指针而是std::size_t数组下标，其中数组指的是Dfa中的nodes。这使Dfa的拷贝变得十分平凡，但还是改变不了我的懒惰——拷贝依然是= delete。makeNode功能上还是创建DfaNode，但是参数非常诡异，后面再讲。

子集是幂集的元素，极端情况下子集构造算法的复杂度为(O(2^n))，因此子集（subset）构造算法又称幂集（powerset）构造算法。

之前提到，NFA中状态之间可以用(varepsilon)转移，它们看起来像是相同的状态，这就是子集构造算法的核心想法。

在详述算法之前，先下个定义：一个状态的(varepsilon)闭包为能从该状态通过(varepsilon)转移到的所有状态的集合。

static void epsClosure(NfaNode* node, std::set<NfaNode*>& set, bool& accept)
{
    if (set.find(node) != set.end())
        return;
    set.insert(node);
    if (node->accept)
        accept = true;
    for (auto&& n : node->eps)
        epsClosure(n, set, accept);
}

static std::pair<std::set<NfaNode*>, bool> epsClosure(NfaNode* node)
{
    std::set<NfaNode*> set;
    bool accept = false;
    epsClosure(node, set, accept);
    return { set, accept };
}

makeNode的第一个参数，正是(varepsilon)闭包这样的状态集合；subsetMap为状态集合到DfaNode指针的映射；makeNode的返回值为std::map::insert的返回值，其中的bool表示是否有新键插入，这个值后面有用。

std::pair<Dfa::SubsetMap::iterator, bool> Dfa::makeNode(const std::set<NfaNode*>& set, bool accept)
{
    auto found = subsetMap.find(set);
    if (found != subsetMap.end())
        return { found, false };
    auto ptr = new DfaNode;
    auto index = nodes.size();
    nodes.push_back(ptr);
    ptr->accept = accept;
    return subsetMap.insert({ set, index });
}

子集构造算法的过程为：

1. 求出起始状态的(varepsilon)闭包，该NFA状态集合对应一个DFA状态，接受属性取决于闭包中是否有接受状态，入队；

2. 取出队列首元素，是一个状态集合，对于(Sigma)中的每一个字符，求出 集合中每一个状态 通过该字母转移到的状态 的(varepsilon)闭包 的并集，对应一个DFA状态，接受属性取决于并集中是否有接受状态（思考：为什么是||的关系？），如果该集合未被处理过，则入队；

3. 如果队列非空，回到2，否则结束。

Dfa nfaToDfa(const Nfa& nfa)
{
    Dfa dfa;
    auto ret = epsClosure(nfa.begin);
    dfa.makeNode(ret.first, ret.second);
    auto start = dfa.subsetMap.begin();
    std::queue<decltype(start)> queue;
    queue.push(start);
    while (!queue.empty())
    {
        auto iter = queue.front();
        queue.pop();
        std::set<char> sigma;
        for (auto&& node : iter->first)
            for (auto&& kv : node->map)
                sigma.insert(kv.first);
        for (auto&& c : sigma)
        {
            std::set<NfaNode*> set;
            bool accept = false;
            for (auto&& node : iter->first)
            {
                auto found = node->map.find(c);
                if (found == node->map.end())
                    continue;
                auto ret = epsClosure(found->second);
                set.insert(ret.first.begin(), ret.first.end());
                accept = accept || ret.second;
            }
            auto pair = dfa.makeNode(set, accept);
            dfa.nodes[iter->second]->map[c] = pair.first->second;
            if (pair.second)
                queue.push(pair.first);
        }
    }
    return dfa;
}

上一个NFA构造出的DFA如图：

已经很复杂了，不是吗？不要慌，后面还有更复杂的。

Hopcroft算法

通过子集构造算法获得的DFA不是最简的。化简一个DFA的手段有删掉不可到达的状态和合并不可区分的状态，上面这个子集构造算法的实现不会产生不可到达的状态，因此只需用Hopcroft算法化简即可（呵，说得轻巧）。

Hopcroft算法的输入与输出都是DFA，输出用Dfa即可表示，但我定义了一个类似的新的数据结构，方便后续优化：

class SimpNode
{
public:
    std::map<char, std::size_t> map;
    bool accept = false;
};

class SimpDfa
{
public:
    SimpDfa();
    SimpDfa(const SimpDfa&) = delete;
    SimpDfa& operator=(const SimpDfa&) = delete;
    SimpDfa(SimpDfa&&) noexcept;
    SimpDfa& operator=(SimpDfa&&) noexcept;
    ~SimpDfa();
    std::size_t begin = 0;
    SimpNode* getNode(std::size_t);
private:
    std::vector<SimpNode*> nodes;
    std::size_t makeNode();
    friend SimpDfa simplifyDfa(const Dfa& dfa);
    friend void generateCode(std::ostream&, const std::string&, const SimpDfa&);
};

SimpDfa::SimpDfa() = default;

SimpDfa::SimpDfa(SimpDfa&& other) noexcept
    : nodes(std::move(other.nodes)), begin(other.begin)
{
    ;
}

SimpDfa& SimpDfa::operator=(SimpDfa&& other) noexcept
{
    nodes.swap(other.nodes);
    begin = other.begin;
    return *this;
}

SimpDfa::~SimpDfa()
{
    for (auto&& p : nodes)
        delete p;
}

SimpNode* SimpDfa::getNode(std::size_t index)
{
    return nodes[index];
}

std::size_t SimpDfa::makeNode()
{
    auto ptr = new SimpNode;
    auto index = nodes.size();
    nodes.push_back(ptr);
    return index;
}

Hopcroft算法的核心是集合划分：

• 初始状态为两个集合，接受状态组成的集合与非接受状态组成的集合；

• 对于每一个集合，我们要考察其中的各个状态是否是不可区分的：对集合中的每一个状态，求出其转移到的状态所在的集合，集合中的所有状态的这一信息必须完全相同——字符与字符对应的集合都相同——才能认为该集合不可划分；否则就根据这一信息来划分，相同的划分为一个新的集合；

• 如果这一步中集合被划分，那么先前被认为是不可划分的集合可能会变得可以划分，需要重新遍历集合的集合，直到一次遍历中没有划分操作；

• 最后，每个集合对应一个化简后DFA的状态，接受属性只需任取集合中一个元素看——很容易证明集合中各状态的接受属性相同；然后根据原DFA的转移计算出新DFA的转移。

这个算法的实现非常猥琐。我们知道并查集（可并集），初始时每个元素都是独立的集合，然后可以把两个集合并起来，时间复杂度接近(O(n))。那么有没有所谓“可分集”呢？

我用的是笨办法，用std::list保存各个集合，包括原DFA与新DFA中的状态，在原DFA中维护指向std::list中元素的迭代器，这样原DFA中的状态与集合可以互相知晓。原DFA中的状态是只读的（为什么不去掉const或者加mutable呢？因为不优雅），无法在其中维护迭代器，因此新开一个std::vector，与nodes中的元素一一对应，这也是DfaNode中用数组下标而不像NfaNode那样用指针的原因（显然，最初的实现是用指针的，后来才改成数组下标）。

struct ListItem
{
    ListItem() = default;
    ListItem(std::set<std::size_t>&& set)
        : indices(std::move(set)) { }
    std::set<std::size_t> indices;
    std::size_t node = 0;
};

struct ItemRef
{
    std::list<ListItem>::iterator iterator;
};

SimpDfa simplifyDfa(const Dfa& dfa)
{
    auto size = dfa.nodes.size();
    std::vector<ItemRef> helper(size);
    std::list<ListItem> list;
    {
        list.emplace_back();
        list.emplace_back();
        auto yes = list.begin();
        auto no = ++list.begin();
        for (decltype(size) i = 0; i != dfa.nodes.size(); ++i)
            if (dfa.nodes[i]->accept)
            {
                yes->indices.insert(i);
                helper[i].iterator = yes;
            }
            else
            {
                no->indices.insert(i);
                helper[i].iterator = no;
            }
        if (no->indices.empty())
            list.erase(no);
    }
    while (1)
    {
        bool ok = true;
        for (auto iter = list.begin(); iter != list.end(); )
        {

            std::map<std::map<char, ListItem*>, std::set<std::size_t>> map;
            for (auto&& i : iter->indices)
            {
                std::map<char, ListItem*> key;
                for (auto&& kv : dfa.nodes[i]->map)
                    key.insert({ kv.first, &*helper[kv.second].iterator });
                map[key].insert(i);
            }
            if (map.size() == 1)
            {
                ++iter;
                continue;
            }
            ok = false;
            for (auto&& pair : map)
            {
                auto& set = pair.second;
                list.emplace_back(std::move(set));
                auto iter = --list.end();
                for (auto&& i : iter->indices)
                    helper[i].iterator = iter;
            }
            iter = list.erase(iter);
        }
        if (ok)
            break;
    }
    SimpDfa result;
    for (auto&& item : list)
    {
        item.node = result.makeNode();
        result.nodes[item.node]->accept = dfa.nodes[*item.indices.begin()]->accept;
    }
    for (decltype(size) i = 0; i != size; ++i)
    {
        auto& map = result.nodes[helper[i].iterator->node]->map;
        for (auto&& kv : dfa.nodes[i]->map)
            map.insert({ kv.first, helper[kv.second].iterator->node });
    }
    result.begin = helper[0].iterator->node;
    return result;
}

上一个DFA化简得DFA如图：

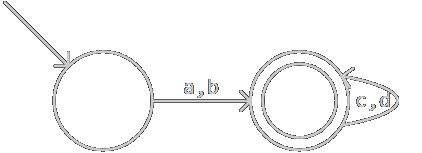
这个例子没有涉及到集合划分的过程，我们换一个wikipedia上的例子：(0|(1(01*(00)*0)*1)*)*，匹配所有能被3整除的二进制数。这里不探讨它的正确性，我更不知道该如何写出这样的正则表达式，只管拿来用就是了。该RE被转换为：

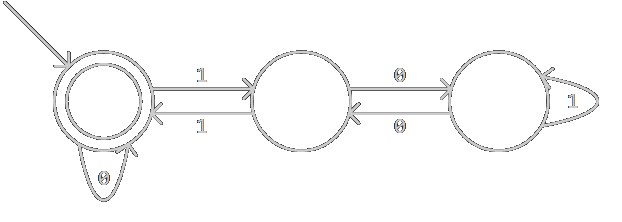
生成C++代码

既然是用C++写的，那就生成C++的代码吧！想起曾经读过的《设计模式》，State模式完全就是为自动状态机而生，趁机实践一下：

#include <iostream>

class Automaton
{
public:
    ~Automaton()
    {
        for (auto&& p : states)
            delete p;
    }
    bool operator()(const std::string& s)
    {
        index = 0;
        for (auto&& c : s)
            (*states[index])(c);
        return states[index]->accept();
    }
private:
    struct State
    {
        Automaton* ptr;
        State(Automaton* ptr)
            : ptr(ptr) { }
        virtual ~State() = default;
        virtual bool accept() = 0;
        virtual void operator()(char) = 0;
    };
    struct StateAccept : State
    {
        using State::State;
        virtual ~StateAccept() override = default;
        virtual bool accept() override final
        {
            return true;
        }
        virtual void operator()(char) override = 0;
    };
    struct StateReject : State
    {
        using State::State;
        virtual ~StateReject() override = default;
        virtual bool accept() override final
        {
            return false;
        }
        virtual void operator()(char) override = 0;
    };
    struct StateError : StateReject
    {
        using StateReject::StateReject;
        virtual ~StateError() override = default;
        virtual void operator()(char c) override final
        {
            ;
        }
    };
    struct State0 : StateAccept 
    {
        using StateAccept::StateAccept;
        virtual ~State0() override = default;
        virtual void operator()(char c) override final
        {
            switch (c)
            {
            case '0':
                ptr->index = 0;
                break;
            case '1':
                ptr->index = 1;
                break;
            default:
                ptr->index = 3;
                break;
            }
        }
    };
    struct State1 : StateReject 
    {
        using StateReject::StateReject;
        virtual ~State1() override = default;
        virtual void operator()(char c) override final
        {
            switch (c)
            {
            case '0':
                ptr->index = 2;
                break;
            case '1':
                ptr->index = 0;
                break;
            default:
                ptr->index = 3;
                break;
            }
        }
    };
    struct State2 : StateReject 
    {
        using StateReject::StateReject;
        virtual ~State2() override = default;
        virtual void operator()(char c) override final
        {
            switch (c)
            {
            case '0':
                ptr->index = 1;
                break;
            case '1':
                ptr->index = 2;
                break;
            default:
                ptr->index = 3;
                break;
            }
        }
    };
    State* states[4] = {
        new State0{this},
        new State1{this},
        new State2{this},
        new StateError{this},
    };
    std::size_t index;
};

int main()
{
    std::cout << std::boolalpha;
    Automaton a;
    std::string input;
    while (std::getline(std::cin, input))
        std::cout << a(input) << std::endl;
}

这是上面最后一张图的代码实现，用作生成代码的模板。State及其子类的关系如图：

void generateCode(std::ostream& os, const std::string& name, const SimpDfa& dfa)
{
    const char* indent = "    ";
    os << "#include <iostream>
"
        << "
"
        << "class " << name << "
"
        << "{
"
        << "public:
"
        << indent << "~" << name << "()
"
        << indent << "{
"
        << indent << indent << "for (auto&& p : states)
"
        << indent << indent << indent << "delete p;
"
        << indent << "}
"
        << indent << "bool operator()(const std::string& s)
"
        << indent << "{
"
        << indent << indent << "index = " << dfa.begin << ";
"
        << indent << indent << "for (auto&& c : s)
"
        << indent << indent << indent << "(*states[index])(c);
"
        << indent << indent << "return states[index]->accept();
"
        << indent << "}
"
        << "private:
"
        << indent << "struct State
"
        << indent << "{
"
        << indent << indent << name << "* ptr;
"
        << indent << indent << "State(" << name << "* ptr)
"
        << indent << indent << indent << ": ptr(ptr) { }
"
        << indent << indent << "virtual ~State() = default;
"
        << indent << indent << "virtual bool accept() = 0;
"
        << indent << indent << "virtual void operator()(char) = 0;
"
        << indent << "};
"
        << indent << "struct StateAccept : State
"
        << indent << "{
"
        << indent << indent << "using State::State;
"
        << indent << indent << "virtual ~StateAccept() override = default;
"
        << indent << indent << "virtual bool accept() override final
"
        << indent << indent << "{
"
        << indent << indent << indent << "return true;
"
        << indent << indent << "}
"
        << indent << indent << "virtual void operator()(char) override = 0;
"
        << indent << "};
"
        << indent << "struct StateReject : State
"
        << indent << "{
"
        << indent << indent << "using State::State;
"
        << indent << indent << "virtual ~StateReject() override = default;
"
        << indent << indent << "virtual bool accept() override final
"
        << indent << indent << "{
"
        << indent << indent << indent << "return false;
"
        << indent << indent << "}
"
        << indent << indent << "virtual void operator()(char) override = 0;
"
        << indent << "};
"
        << indent << "struct StateError : StateReject
"
        << indent << "{
"
        << indent << indent << "using StateReject::StateReject;
"
        << indent << indent << "virtual ~StateError() override = default;
"
        << indent << indent << "virtual void operator()(char c) override final
"
        << indent << indent << "{
"
        << indent << indent << indent << ";
"
        << indent << indent << "}
"
        << indent << "};
";
    auto size = dfa.nodes.size();
    for (decltype(size) i = 0; i != size; ++i)
    {
        using namespace std::string_literals;
        auto& node = *dfa.nodes[i];
        auto className = "State" + std::to_string(i);
        auto baseName = "State"s + (node.accept ? "Accept" : "Reject");
        os << indent << "struct " << className << " : " << baseName << " 
"
            << indent << "{
"
            << indent << indent << "using " << baseName << "::" << baseName << ";
"
            << indent << indent << "virtual ~" << className << "() override = default;
"
            << indent << indent << "virtual void operator()(char c) override final
"
            << indent << indent << "{
"
            << indent << indent << indent << "switch (c)
"
            << indent << indent << indent << "{
";
        for (auto&& kv : node.map)
            os << indent << indent << indent << "case '" << kv.first << "':
"
                << indent << indent << indent << indent << "ptr->index = " << kv.second << ";
"
                << indent << indent << indent << indent << "break;
";
        os << indent << indent << indent << "default:
"
            << indent << indent << indent << indent << "ptr->index = " << size << ";
"
            << indent << indent << indent << indent << "break;
"
            << indent << indent << indent << "}
"
            << indent << indent << "}
"
            << indent << "};
";
    }
    os << indent << "State* states[" << size + 1 << "] = {
";
    for (decltype(size) i = 0; i != size; ++i)
        os << indent << indent << "new State" << std::to_string(i) << "{this},
";
    os << indent << indent << "new StateError{this},
"
        << indent << "};
"
        << indent << "std::size_t index;
"
        << "};
"
        << "
"
        << "int main()
"
        << "{
"
        << indent << "std::cout << std::boolalpha;
"
        << indent << "Automaton a;
"
        << indent << "std::string input;
"
        << indent << "while (std::getline(std::cin, input))
"
        << indent << indent << "std::cout << a(input) << std::endl;
"
        << "}
";
}

代码当然不是手敲的，先在编辑器中替换，再把要更改的部分换成变量即可。

至此，从正则表达式到C++代码的转换终于实现了。

后记

本文介绍的算法大多涉及比较复杂的数据结构，复杂程度刷新了我的记录，以致于我一直在思考是不是我的想法太复杂了？其实有时想得简单也会导致问题变得复杂，比如我一开始把子集构造算法中状态集合的转移误认为对每一个转移求闭包而不取并集（网课没有讲清楚是一方面），然后std::map的值类型就从T变为std::vector<T>或std::set<T>，实现更加复杂，而且出现了错误！如果一个状态对一个字符有多条转移，DFA的“D”体现在哪了呢——写一个算法发现不对劲的时候，也许是对前导算法的理解有误。

最好的办法是对每一个算法加以严谨的证明，顺便求出最坏和平均复杂度，然而与算法有关的数学我都不太懂，本文也没有那么远大的目标。如果想了解详情，还请参考专业资料。

以上实现还有很多改进空间。比如，NfaNode中的accept是不必要的，可以以数组下标的形式放入Nfa中，为每个NfaNode对象节省4字节空间。Thompson构造法的实现也可以优化，减少NFA状态与(varepsilon)转移的数量有助于减少epsClosure的递归深度，增加一些代码来换取运行时性能还是值得的，只不过我又一次犯懒了。

这一套算法的正则表达式输入部分，或许可以称为“前端”，可以增加对RE语法糖的支持，使算法能处理通用的、友好的RE，这是可扩展性的体现；然而局限也十分明显，生成代码只能对输入字符串回答是否接受，而不能给出匹配的具体信息，从而无法作为通用的编程工具。C++11引入了regex库，有机会去学习学习。