数据衰减的一些方法和比较
在计算机视觉实时应用中,有时候需要向云台发送一些数据,比如说角度,使之运动到相应的角度。但是考虑到有时候如果直接发送目标的相对角度,可能角度比较大,从而导致云台运动过于剧烈,此时考虑将发送的数据做一个衰减。
一般直接想到对发送的数据做线性衰减,比如说发送数据yaw:
yaw /= 10;
这样做能达到目的,但是对于所有数据都做了相同的衰减,对于很小的数,也是和很大的数据一样,做了除以10 的衰减。
换一种方式,做分段函数的线性衰减:
if(abs(yaw) > 2)
yaw /= 10;
else
yaw /= 5;
这样对于很大的数和很小的数做了不一样的衰减操作,似乎比上一种方法更有效。但是考虑一下分界线周围的情况,对于yaw=2.2,返回的是2.2/10 = 0.22,但是对于yaw=1.8返回的是1.8/5=0.36。一个更大的数返回了一个更小的数,似乎也是不太合理。
再换一种方式,做指数衰减:
yaw = (yaw >= 0) ? log2(abs(yaw) + 1) : -log2(abs(yaw) + 1);
上面两个衰减遇到的问题都解决了。当然可以再调整复杂一点,另外指数衰减的底数也需要根据实际应用做出选择。但是这种方法也有一定的缺点,比如说计算过于耗时,计算机对于log函数的计算消耗的时钟周期远大于做除法消耗的时钟周期。有人做过比较(链接):
- 0)开根号运算需要时钟周期数为:22;
- 1)加、减、乘、除法运算的时钟周期数为:4;
- 2)log运算的时钟周期数为:92。
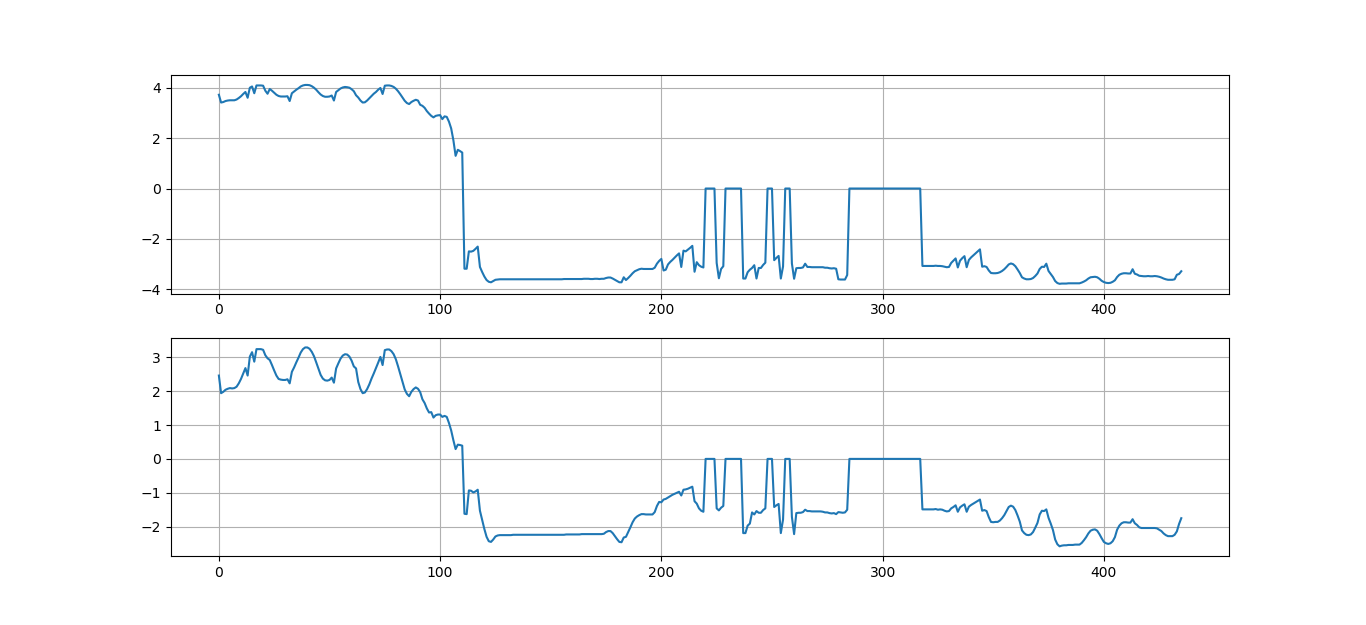
一张效果图对比(上图采用log衰减,下图采用分段函数线性衰减,log衰减的抖动明显小,不过幅度稍大(采用log2),见区间【0, 100】):