2012-2013 ACM-ICPC, NEERC, Central Subregional Contest J Computer Network1 （缩点+最远点对）

题意：在连通图中，求一条边使得加入这条边以后的消除的桥尽量多。

在同一个边双连通分量内加边肯定不会消除桥的，

求边双连通分量以后缩点，把桥当成边，实际上是要选一条最长的链。

缩点以后会形成一颗树，一定不存在环否则和桥的定义矛盾，求树上的最远点对。

树上的最远点对用dp TLE了，实际上两次dfs就行了，第一次随便选一个点dfs找到最远的点，

再从那个点dfs找最远的点就是树上的最远点对，为什么这样是对的呢？反向来构造，假设已经找了最长的链，

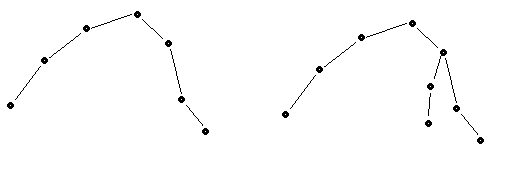
往链上某点上添加一条链，这条链的长度一定小于这个点到两个端点之中距离的最小的那个，

因此无论从哪个点出发dfs，一定会到达最长的链的一个端点。第二遍就一定能找到最长的链。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e4+5, maxm = 2e5+5;
int head[maxn],nxt[maxm],to[maxm],ecnt;

void addEdge(int u,int v)
{
    to[ecnt] = v;
    nxt[ecnt] = head[u];
    head[u] = ecnt++;
}


int pre[maxn],low[maxn],dfs_clock;
bool cut[maxm];

void tarjan(int u,int fa)
{
    pre[u] = low[u] = ++dfs_clock;
    for(int i = head[u]; ~i; i = nxt[i]){
        int v = to[i];
        if(!pre[v]){
            tarjan(v,i);
            low[u] = min(low[u],low[v]);
            if(low[v] > pre[u]){
                //if(fa<0) cut[i] = cut[i^1] = ~nxt[head[u]];
                //else
                cut[i] = cut[i^1] = true;
            }
        }else if( (i^1)!=fa && pre[v] < pre[u]){
            low[u] = min(pre[v],low[u]);
        }
    }
}

int eccno[maxn],ecc_cnt;
int pid[maxn];
void dfs(int u)
{
    eccno[u] = ecc_cnt;
    for(int i = head[u]; ~i; i = nxt[i] ) if(!cut[i]){
        if(!eccno[to[i]]) dfs(to[i]);
    }
}

vector<int> G[maxn];
#define PB push_back
int deg[maxn];

void find_ecc(int n)
{
    dfs_clock = 0;
    tarjan(0,-1);
    ecc_cnt = 0;
    for(int i = 0; i < n; i++){
        if(!eccno[i]){
            ecc_cnt++;
            pid[ecc_cnt] = i;
            dfs(i);
        }
    }

    for(int i = 1; i <= ecc_cnt; i++) G[i].clear();
    memset(deg,0,sizeof(deg));
    for(int i = 0; i < ecnt; i+=2){
        if(cut[i]){
            int u = eccno[to[i]], v = eccno[to[i^1]];
            G[u].PB(v); G[v].PB(u);
            deg[u]++; deg[v]++;
        }
    }
}

void init()
{
    memset(head,-1,sizeof(head));
    ecnt = 0;
}

int MaxD,poi;

void dfs(int u,int fa,int d)
{
    if(d > MaxD){
        MaxD = d;
        poi = u;
    }
    for(int i = 0; i <(int)G[u].size(); i++){
        int v = G[u][i]; if(v == fa) continue;
        dfs(v,u,d+1);
    }
}

void solve()
{
    MaxD = 0; poi = 1;
    dfs(1,-1,0);
    int u = poi;
    MaxD = 0; poi = u;
    dfs(u,-1,0);
    int v = poi;
    printf("%d %d
",pid[u]+1,pid[v]+1);
}

int main()
{
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    int n,m;scanf("%d%d",&n,&m);
    init();
    for(int i = 0; i < m; i++){
        int u,v; scanf("%d%d",&u,&v); u--;v--;
        addEdge(u,v); addEdge(v,u);
    }
    find_ecc(n);
    solve();
    return 0;
}